1.2.7. Переход от модели системы в переменных состояниях к матричной передаточной функции

При нулевых начальных условиях уравнение (1.81) можно преобразовать по Лапласу в виде:

pX(p) = AX(p) + Bu(p);

Y(p) = CX(p). (1.98)

Откуда получим

Y(p) = C[pI – A]^1Bu(p). (1.99)

Тогда имеем

W(p) = C[pI – A]^1B, (1.100)

которая называется матричной передаточной функцией системы управления.

1.3. Основные динамические звенья и их соединения

1.3.1. Элементарные динамические звенья

Динамическим звеном называют часть системы, описываемую дифференциальным (или интегральным) уравнением. В общем случае порядок уравнения может быть произвольным. В связи с этим есть смысл выделить элементарные звенья, через которые можно представить сложные звенья или даже системы управления. Почти все реальные системы, у которых порядок числителя меньше порядка знаменателя, можно разложить на звенья следующих типов: интегрирующие, дифференцирующие, усилительные (безинерционные), инерционные первого, второго порядка, интегро-дифференцирующие, запаздывающие (задерживающие сигналы) и иррационные.

Рассмотрим основные характеристики некоторых звеньев.

Интегрирующее звено можно записать в виде

, (1.101) где y  выходной сигнал; x  входной сигнал звена.

Весовая функция

q(t) = b. (1.102)

Передаточная функция

. (1.103)

Частотная передаточная функция

(1.104)

совпадает с осью мнимых составляющих. С увеличением  амплитуда выходного сигнала стремиться к нулю. Звено обеспечивает фазовый сдвиг выходного сигнала на .

Дифференцирующее звено формирует выходную переменную y(t) в виде производной входной переменной

. (1.105)

Переходная функция

h(t) = b(t). (1.106)

Весовая функция

. (1.107)

Передаточная функция звена

W(p) = bp. (1.108)

Частотная передаточная характеристика

W(j) = jb. (1.109)

Фазовая характеристика

. (1.110)

Реальные дифференцирующие звенья обладают инерционными свойствами, которые искажают результат дифференцирования быстроменяющихся входных сигналов. Примером звена, близкого к дифференцирующему, может служить тахогенератор, предназначенный для дифференцирования угла поворота валов машин, например, электрических.

Апериодическое (инерционное) звено 1-го порядка описывается дифференциальным уравнением первого порядка

. (1.111)

Переходная функция

. (1.112)

Весовая функция

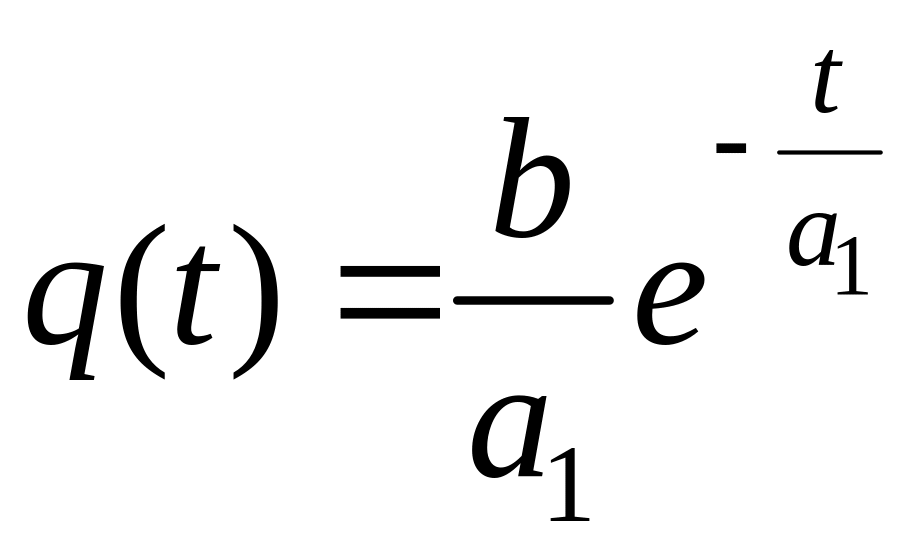. (1.113)

Передаточная функция звена

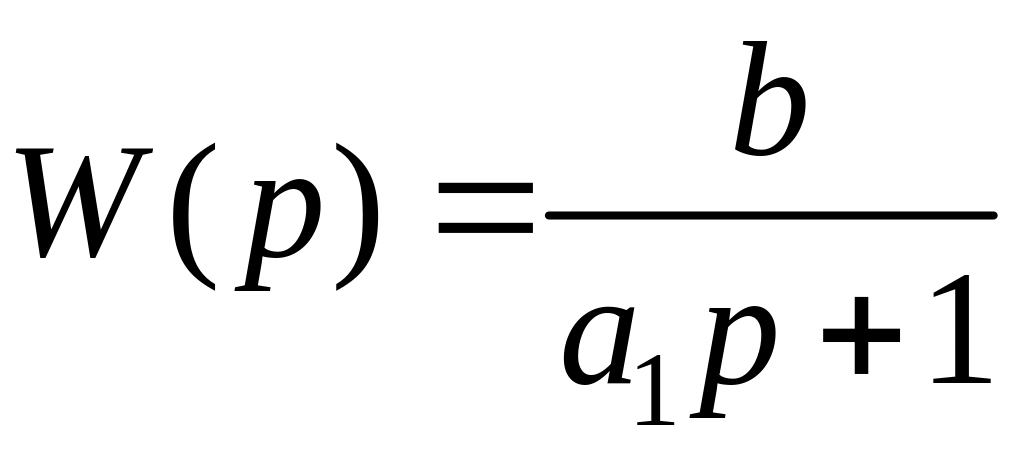. (1.114)

Частотная передаточная характеристика звена имеет вид

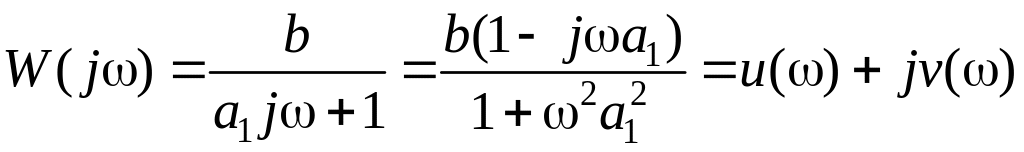. (1.115)

Комплексно-частотная характеристика (КЧХ) апериодического (инерционного) звена приведена на рис. 1.5. для частот [0, ].

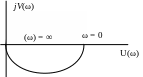
Рис. 1.5. График КЧХ звена 1-го порядка

Характеристика имеет вид полуокружности с центром на вещественной оси с радиусом, равным .

Звено второго порядка описывается дифференциальным уравнениям 2-го порядка, вида

. (1.116)

Если корни его характеристического уравнения являются комплексными и имеют следующий вид:

p₁ =  + j;

p₂ =   j,

то такое звено называется колебательным.

Для такого звена часто коэффициенты a₂ и a₁ в уравнении (1.116) заменяют на a₂ = T², a₁ = 2T,   1. При единичном воздействии получим переходную функцию

, (1.117)

где .

Весовая функция

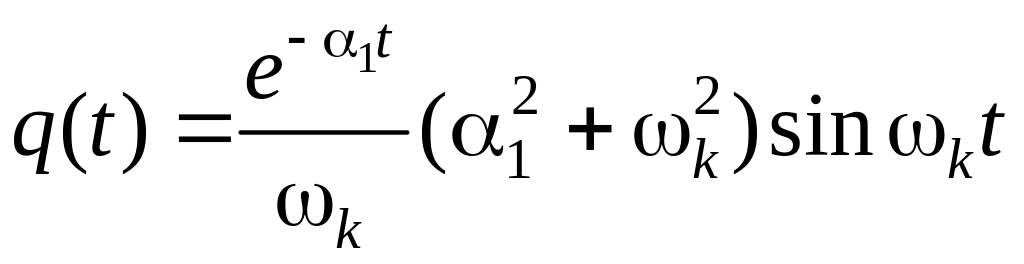. (1.118)

Передаточная функция звена

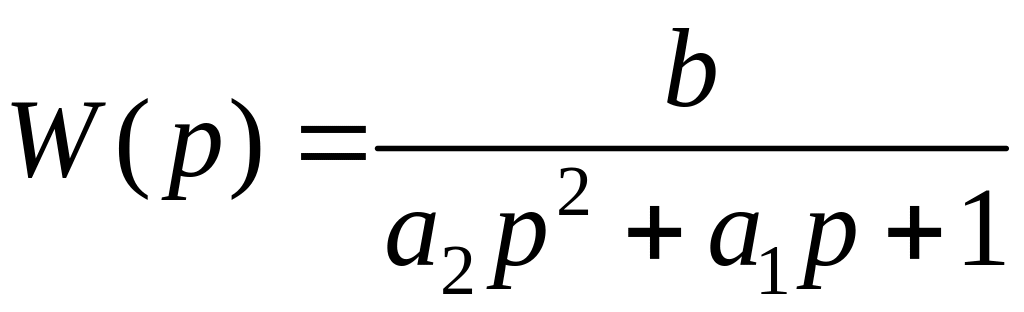(1.119)

Частотная передаточная характеристика

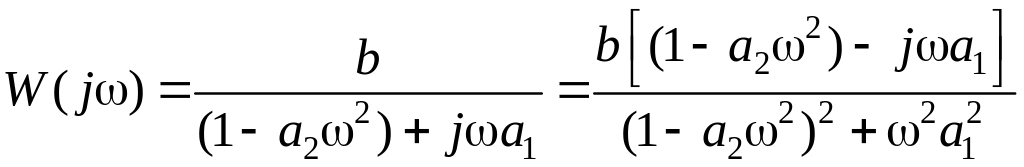. (1.120)

КЧХ звена для [0, ] имеет следующий вид (рис. 1.6.).

Рис. 1.6. График КЧХ колебательного звена 2-го порядка

Апериодическое (инерционное) звено 2-го порядка описывается уравнением (1.117) и отличается от колебательного тем, что корни характеристического уравнения p₁, p₂ вещественны, отрицательны и различны.

Переходная функция

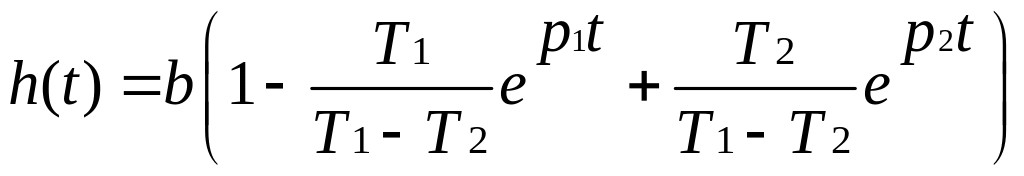, (1. 121)

где  постоянные времени.

Весовая функция

.

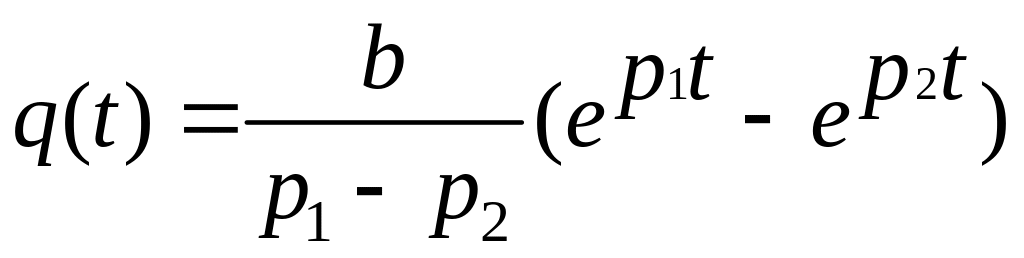Передаточная и частотная функция имеют тот же вид, что и для колебательного звена см. уравнения (1.119) и (1.120).

Если корни уравнения (1.117) p₁ = p₂ = p вещественны, отрицательные и равные, то передаточная функция имеет вид

. (1.122)

Весовая функция

,

где .

Усилительное (безинерционное) звено описывается уравнением

. (1.123)

Переходная функция

. (1.124)

Весовая функция

. (1.125)

Передаточная и частотная функция

; . (1.126)

Звено запаздывания описывается уравнением

, (1.127)

где  − время запаздывания.

Переходная функция

. (1.128)

Весовая функция

. (1.129)

Для нахождения передаточной функции представим x(t – ) в виде ряда разложения относительно базового значения x(t):

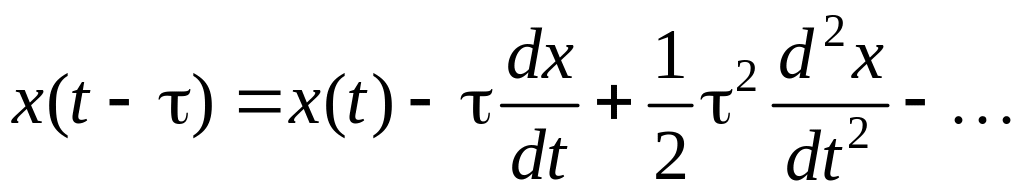(1.130)

Подставив (1.130) в уравнение (1.127) и выполнив преобразование Лапласа, получим

. (1.131)

Ряд в уравнении (1.132) сходится к e^p, что позволяет записать передаточную функцию

. (1.132)

Комплексно-частотная характеристика имеет вид

. (1.133)

График КЧХ имеет вид окружности (рис. 1.7).

Рис. 1.7. График КЧХ звена запаздывания

Фазовый сдвиг выходного сигнала относительно входного равен ().

Инерционно-форсирующее (интегро-дифференцирующее) звено можно представить дифференциальным уравнением вида

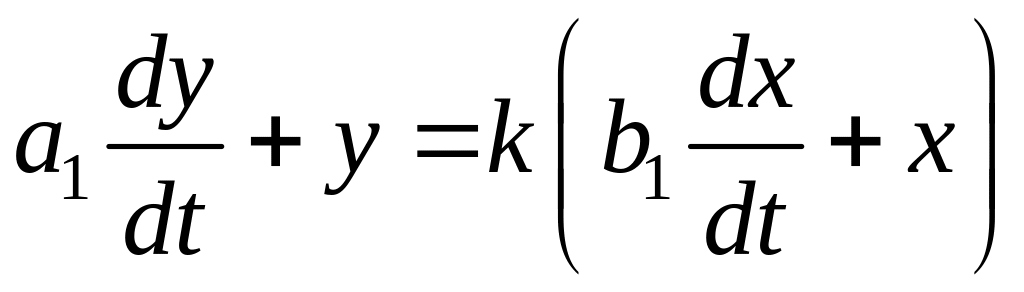. (1.134)

Если при этом b₁ > a₁, то звено называется звеном быстрого реагирования (ЗБР), если b₁ < a₁, то звено называется звеном медленного реагирования (ЗМР).

Передаточная функция звена

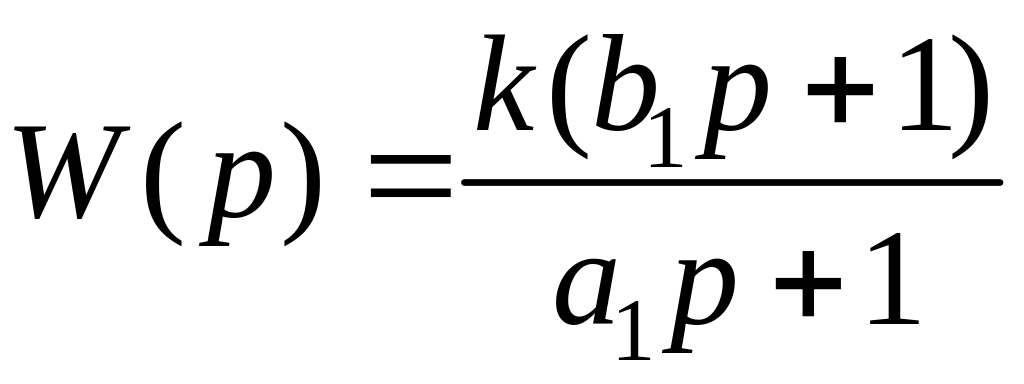. (1.135)

Переходная функция определяется уравнением (1.136) как

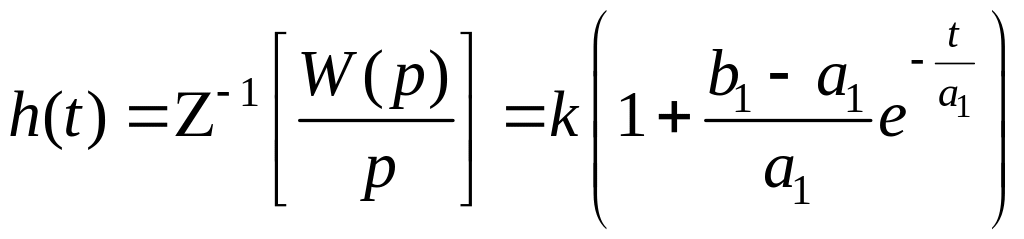. (1.136)

Весовая функция

. (1.137)

Комплексно-частотная характеристика (КЧХ)

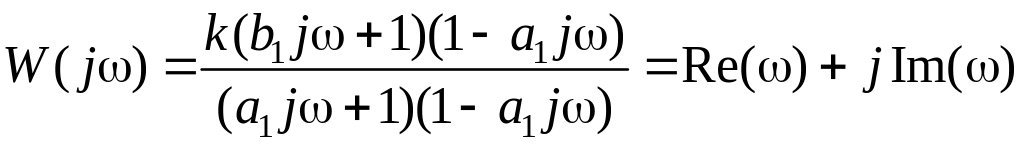. (1.138)

Иррациональные звенья соответствуют семейству звеньев с распределенными параметрами. В общем случае для одномерной распределенности вдоль координаты l имеем дифференциальное уравнение вида

, (1.139)

где Q(l, t) выходная переменная.

Дифференциальное уравнение (1.140) совместно с краевыми условиями описывает поведение системы. Краевые условия включают в себя пространственное распределение параметра в начальный момент времени и законы взаимодействия между элементом и окружающей средой на границе. Если преобразовать уравнение (1.140) по Лапласу при нулевых начальных условиях, то получим

. (1.140)

Выражение (1.141) может быть проинтегрировано типовым приемом

, (1.141)

где .

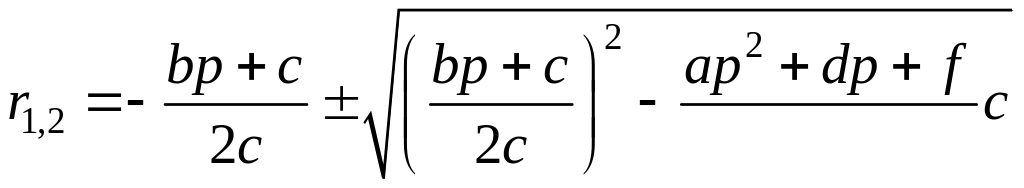Для определения постоянных интегрирования C₀(p) и C₁(p) должны быть известны два преобразованных по Лапласу краевых условия: Q_вх1(p) и Q_вх2(p), которые в частном случае могут выступить как две входные переменные. В линейных динамических системах постоянные интегрирования являются линейными комбинациями граничных условий:

C₀(p) = C₀₁(p)Q_вх1(p) + C₀₂(p)Q_вх2(p);

C₁(p) = C₁₁(p)Q_вх1(p) + C₁₂(p)Q_вх2(p).

Вместо уравнения (1.142) можно написать

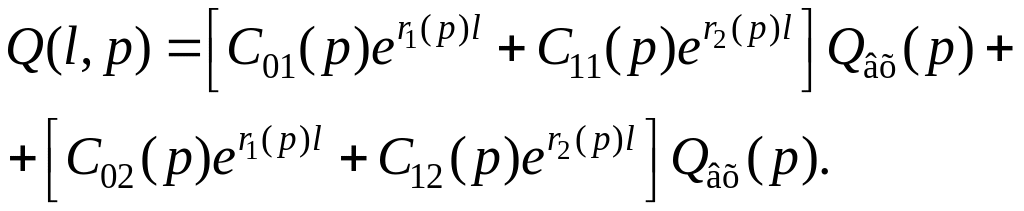(1.142)

Введем обозначения передаточных функций:

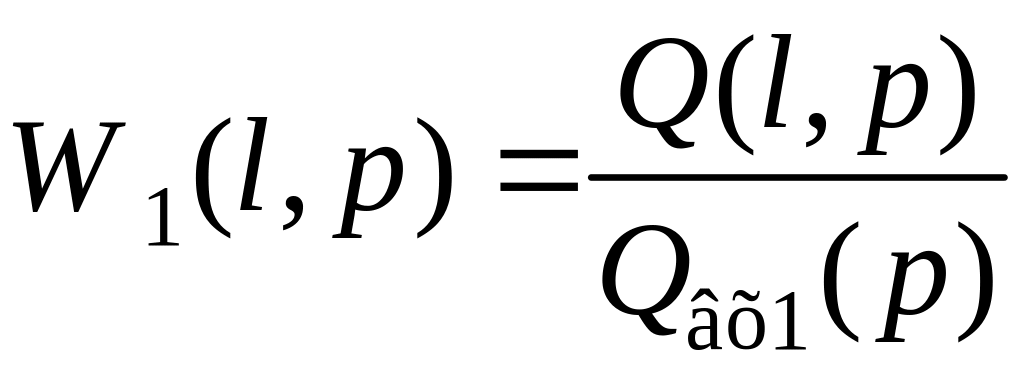при Q_вх2(p) = 0 (1.143)

и

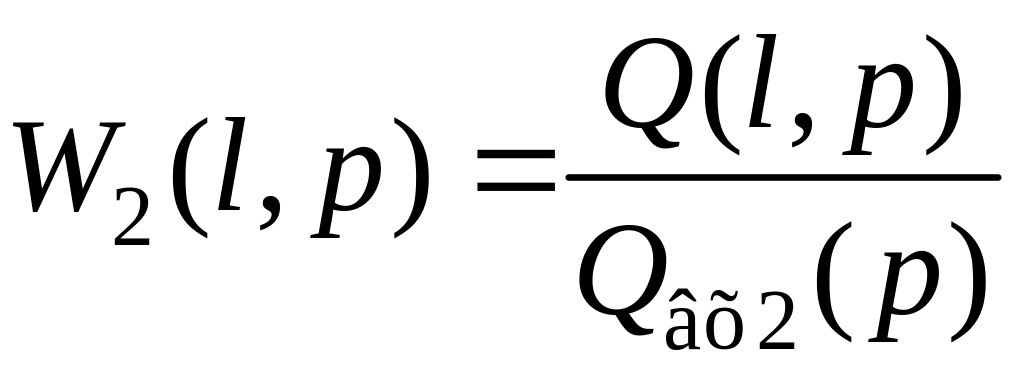при Q_вх1(p) = 0. (1.144)

Корни r₁(p), r₂(p) для многих уравнений с распределенными параметрами требуют извлечения корня квадратного из оператора р, что и порождает наименование таких элементов.