1.2. Описание линейных систем
1.2.1. Описание во временной области
Наиболее полное описание линейной системы состоит из линейного дифференциального уравнения вида
,
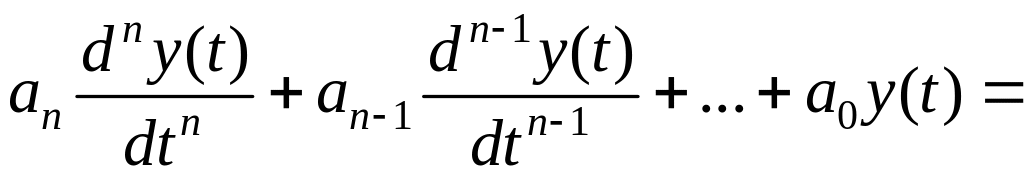
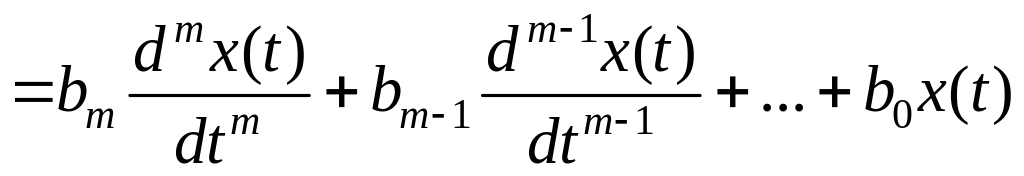(1.40)
где а0,…, аn-1, аn, b0,…, bm-1, bm – коэффициенты (постоянные или переменные во времени); n и m – целые числа (n ≥ 0, m ≥ 0, n ≥ m); y(t) и x(t) – соответственно выход и вход системы (звена). Число n называется порядком уравнения (порядком системы).
Уравнение (1.40) удобно записывать в сокращенной, операторной форме. Введем оператор дифференцирования D, который обладает таким свойством, что умножение на D эквивалентно дифференцированию во времени, т. е. для любой функции f(t)
.
Повторное умножение на D эквивалентно повторному дифференцированию
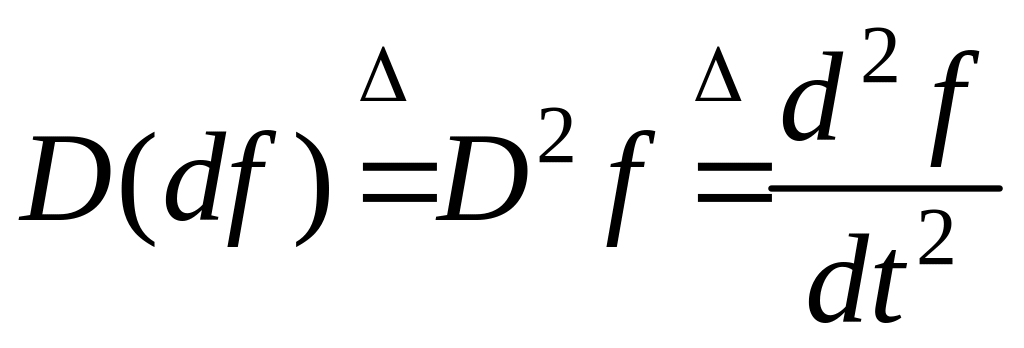
и вообще для любого целого k ≥ 0
.
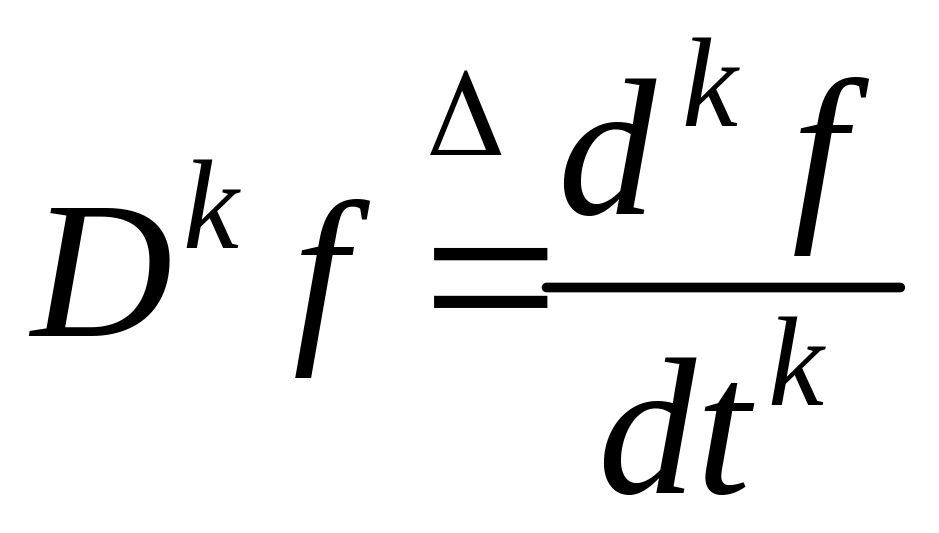(1.41)
С использованием операторных обозначений уравнение (1.40) записывается в виде
(1.42)
или в более сжатой форме
,
(1.43)
где введены обозначения
;
(1.44)
.
(1.45)
1.2.2. Весовые функции
Если разложить действующее на систему воздействие x(t) на элементарные импульсы, используя соотношения (1.8) и формулу (1.38), то можно записать:
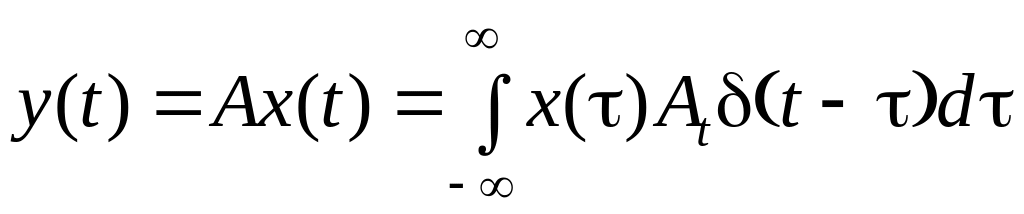(1.46)
где индекс t у оператора A показывает, что этот оператор действует на функцию с аргументом t. Формула (1.46) показывает, что для нахождения реакции линейной системы на произвольное воздействие x(t) достаточно знать ее реакцию на единичный импульс (t ). Эта реакция зависит от переменных t, τ, и ее можно записать в виде
.
(1.47)
Функция q(t, τ), определяемая формулой (1.47), называется весовой функцией. Весовая функция линейной системы представляет собой реакцию этой системы в момент t на единичный импульс, действующий на систему в момент τ. Пользуясь понятием весовой функции, мы можем записать зависимость (1.46) между входной и выходной переменными произвольной линейной системы в виде
.
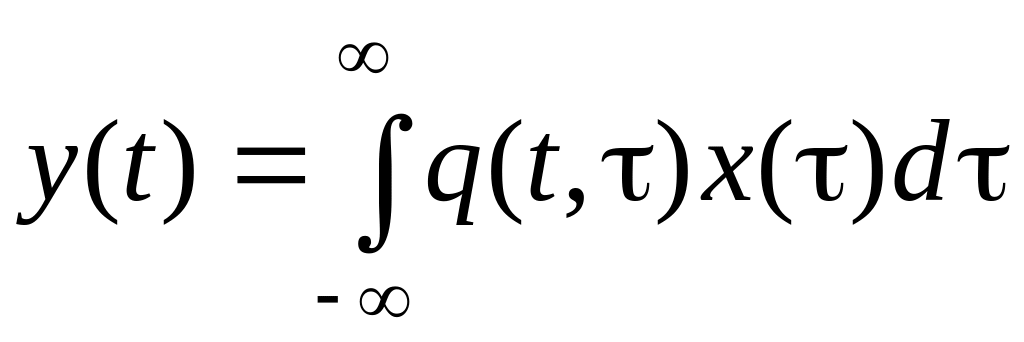(1.48)
Таким образом, оператор любой линейной системы может быть представлен в форме линейного интегрального оператора.
Согласно формуле (1.48), для определения значения выходной переменной линейной системы в момент времени t необходимо значение x(τ), которое имело входное воздействие x(t) в момент τ, умножить на ординату весовой функции q(t, τ) при данном значении t и все подобные произведения просуммировать. Таким образом, весовая функция q(t,τ) характеризует удельный вес воздействия x в момент времени τ на формирование выходной переменной Y в текущий момент времени t.
Весовая функция реальной системы равна нулю при значении второго аргумента, большем значения первого:
при
τ
> t
. (1.49)
Это свойство называют условием физической осуществимости. Никакая система, весовая функция которой не удовлетворяет этому условию, физически немыслима.
Для физически возможной линейной системы, которая находится в покое до момента времени t0, можно сузить пределы интегрирования в уравнении (1.49)
.
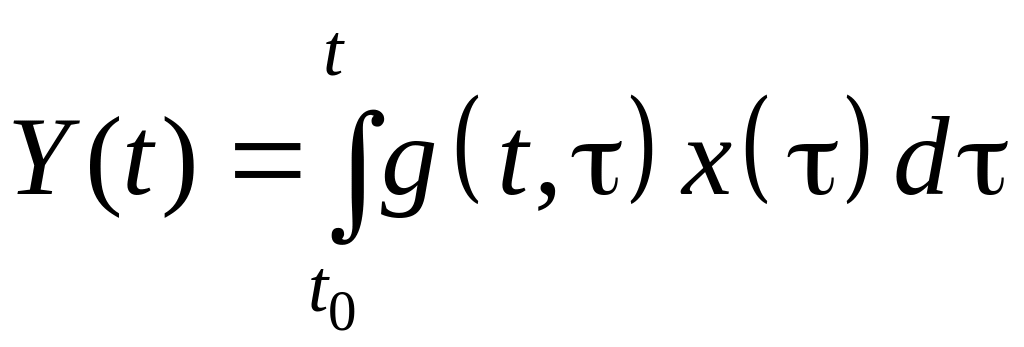(1.50)
Рассмотрим пример нахождения весовой функции. Пусть система описывается дифференциальным уравнением a1y' + a0y = bx.
Если
задать входной сигнал х
в виде единичного импульса (t
),
то
по определению выходной сигнал у
представляет весовую функцию g(t,
).
В результате запишем
.
Интегрируя уравнение при условии, что
система является физически реализуемой,
имеем:
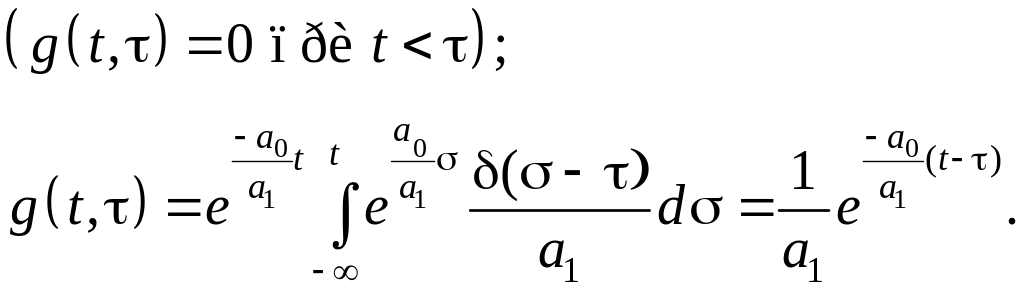
С весовой функцией связана переходная характеристика. Реакция системы на воздействие типа 1(t) называется переходной характеристикой h(t). В силу (1.50) она является интегралом от весовой функции
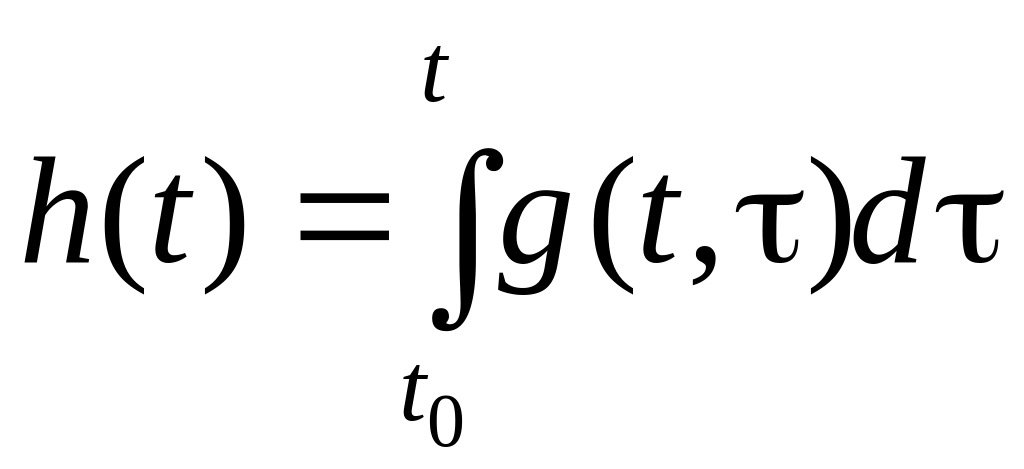(1.51)
или производная от h(t) равна весовой функции
.
(1.52)