1.1.4. Спектральная плотность стационарных процессов

Рассмотрим энергетическую форму интеграла Фурье относительно некоторой случайной функции времени U(t) на основе переходов от U(t) к изображению Фурье

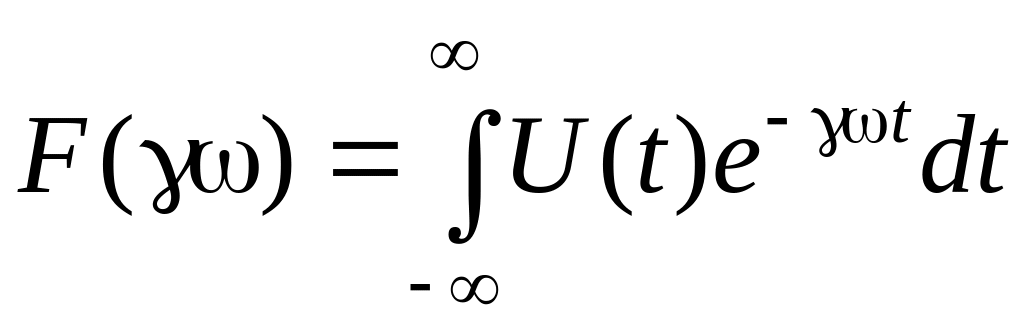(1.25)

и обратно

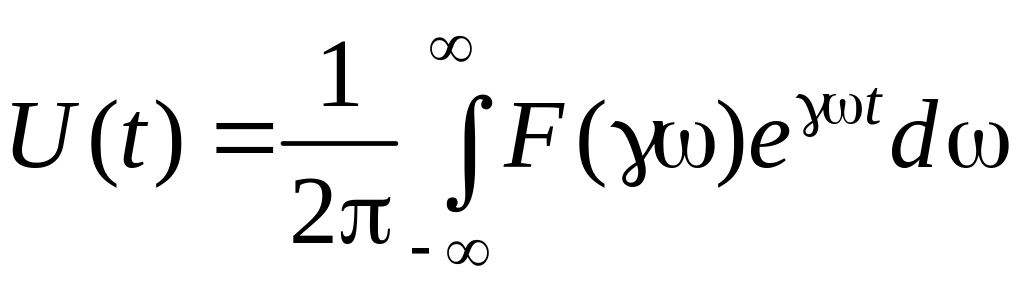. (1.26)

Возьмем квадрат модуля изображения Фурье |F(|² и проинтегрируем по всем частотам от  до  с делением результата на 2:

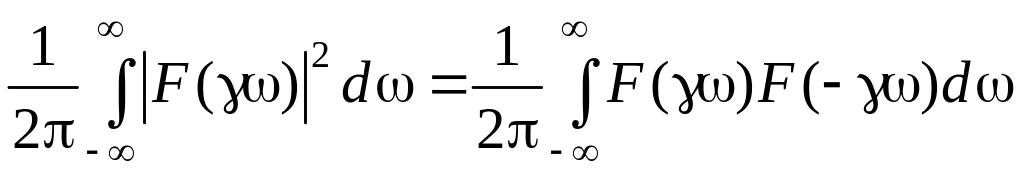. (1.27)

Изображение Фурье F()заменим соотношением (1.25)

. (1.28)

Заменив порядок интегрирования в выражении (1.28), получим

. (1.29)

Выражение в квадратных скобках (1.29) является согласно (1.26) исходным сигналом – u(t). В результате имеем

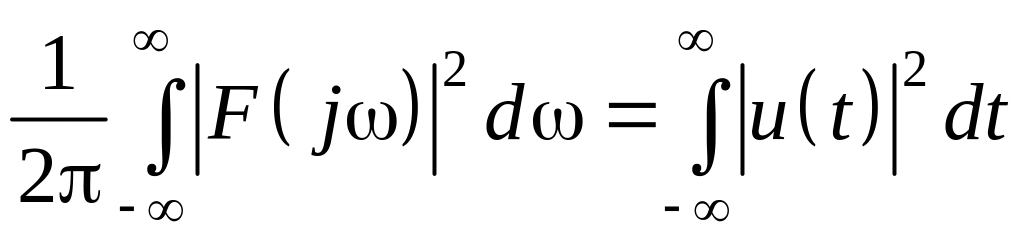. (1.30)

Выражение (1.30) называют формулой Релея, которая соответствует энергетической форме интеграла Фурье. Для нахождения энергии рассматриваемого процесса вместо бесконечного интервала наблюдения с равным основанием можно интегрировать квадрат функции времени по всему интервалу [∞, ∞] или интегрировать квадрат модуля изображения Фурье по всем частотам [∞, ∞]. Для большинства процессов энергия за бесконечный интервал стремится к бесконечности, что неудобно в технических приложениях. В связи с этим удобнее вместо энергии использовать среднюю мощность процесса, которая будет получена, если энергию поделить на интервал наблюдения, тогда на основании формулы (1.30) получим

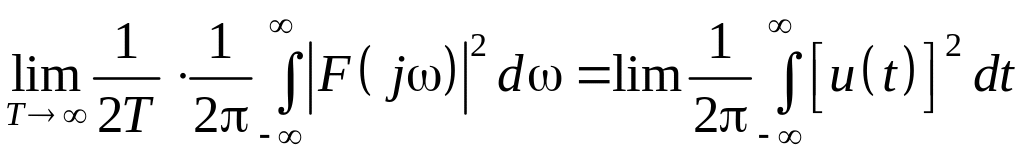. (1.31)

Введем обозначение

, (1.32)

которое получило название спектральной плотности.

С учетом (1.32) перепишем выражение (1.31)

, (1.33)

где ū² – средний квадрат рассматриваемой величины u(t).

Важным свойством спектральной плотности является то, что интегрирование ее по частотам [∞, ∞] дает средний квадрат исходной функции времени u(t). По своему физическому смыслу спектральная плотность есть величина, которая пропорциональна средней мощности процесса в интервале частот от ω до ω + dω.

Спектральная плотность и корреляционная функция случайных процессов представляют собой взаимные преобразования Фурье:

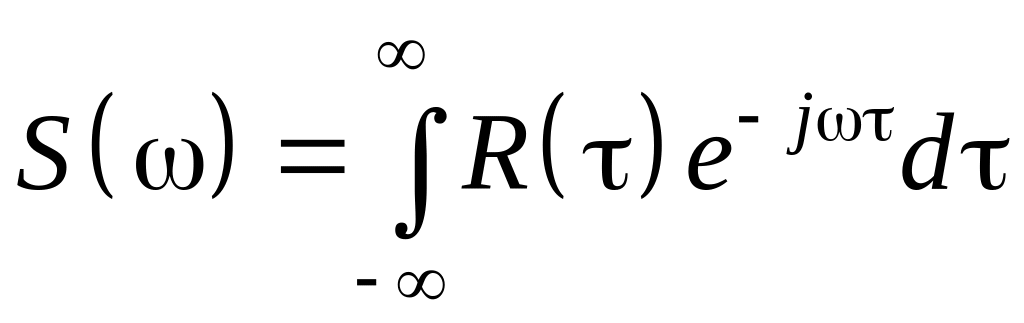; (1.34)

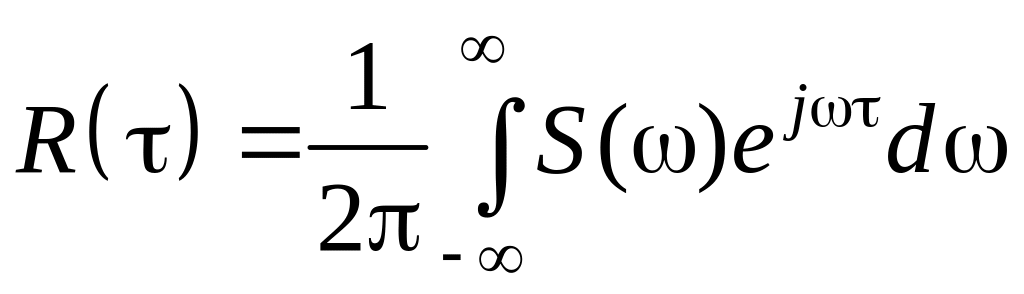. (1.35)

Так как спектральная плотность и корреляционная функция представляют собой четные общественные функции, то иногда формулы (1.34) и (1.35) представляют в более простом виде:

; (1.36)

. (1.37)

Связь между спектральной плотностью S и видом функции времени u(t) заключается в том, что чем уже график S(ω), тем медленнее изменяется величина u(t), и наоборот.

1.1.5. Операторы системы управления

Объекты и системы управления состоят из элементов, имеющих различную природу. Описание каждого элемента обычно дается на языке соответствующей научной дисциплины (электротехника, гидравлика, теплотехника и т.д.). Для анализа их взаимодействия удобно перейти к единообразному описанию. В инженерной практике наибольшее распространение получил следующий способ:

• каждый реальный элемент рассматривается как устройство, звено системы, осуществляющее преобразование одного процесса, называемого входным воздействием, в другой, называемый выходной реакцией или просто преобразованием «вход-выход»;

• взаимодействия между звеньями задаются путем описания связей между их входами и выходами, определяющих их структуру.

Универсальным языком теоретического естествознания, служащим для математического моделирования взаимосвязей процессов в природе и технике, является язык уравнений − алгебраических, и особенно дифференциальных.

Выходной сигнал детерминированной системы является определенной функцией ее входного сигнала. Однако функцию в данном случае надо понимать не в том смысле, в котором она понимается в элементарном математическом анализе, а в обобщенном смысле, так как аргументом функции служит некоторая функция − входной сигнал системы, а значением аргумента (входном сигнале) тоже служит некоторая функция времени  выходной сигнал системы.

В общем случае функцией называется обозначенное соответствие между любыми объектами − элементами двух множеств X и Y, когда каждому элементу x множества Х соответствует один вполне определенный элемент у множества Y. При этом элементами множеств Х и Y могут быть любые объекты. Функция, которая любому значению аргумента Х ставит в соответствие некоторый элемент у множества Y, не являющегося множеством чисел, называется оператором. Так как любая система осуществляет преобразование функций: каждой данной функции на входе ставит в соответствие определенную функцию на выходе, то каждой детерминированной системе соответствует вполне определенный оператор, который называют оператором системы. Оператор системы обычно обозначают одной буквой. Тогда соответствие между входной функцией системы Х(t) и ее выходной функцией Y(t) можно записать в виде

Y(t) = AX(t), (1.38)

где А – оператор системы, который отвечает за всю совокупность математических действий над входной функцией X(t).

Оператор системы является ее полной характеристикой. При этом понятием оператора объединяются любые математические действия: алгебраические, дифференцирование, интегрирование, сдвиг во времени, решение любых функциональных уравнений, а также логические.

Оператор системы может быть задан в различных формах.

В задачах практики поведение автоматической системы часто можно описать конечным числом обыкновенных дифференциальных уравнений. В таких случаях оператор системы сводится к операции решения дифференциальных уравнений. На практике встречаются системы, поведение которых описывается уравнениями в частных производных или более сложными уравнениями. Поэтому аппарат теории дифференциальных уравнений недостаточен для построения общей теории автоматических систем, что вызывает необходимость характеризовать автоматическую систему обобщенным понятием − оператор и пользоваться различными способами задания оператора. Оператор А называется линейным, если при любых числах n, c₁,…, c_n и при любых функциях x₁(t),…, x_n(t) выполняется соотношение

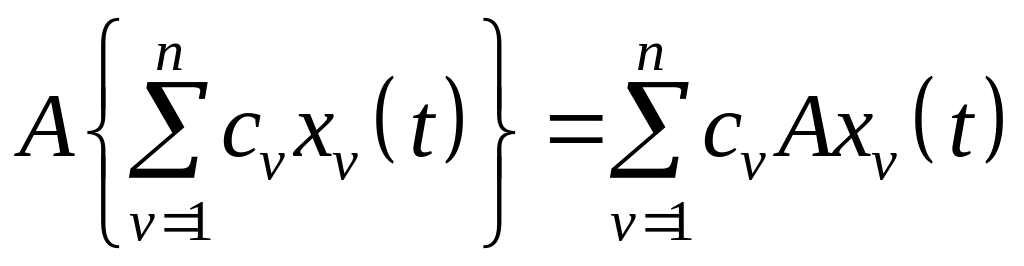. (1.39)

Действие оператора А на любую линейную комбинацию данных функций является линейной комбинацией результатов его действия на каждую функцию в отдельности с теми же коэффициентами.

Система называется линейной, если ее оператор линеен. Свойство линейных систем, выраженное формулой (1.39), называется принципом суперпозиции. Для того чтобы система управления была линейной необходимо и достаточно выполнение следующих условий:

• сумме любых двух входных воздействий соответствует сумма двух выходных переменных;

• при любом усилении входного воздействия без изменения его формы, выходная переменная претерпевает точно такое же усиление, не изменяя своей формы.

Нелинейным называется любой оператор, для которого принцип суперпозиции не имеет места или справедлив только при некоторых вполне определенных функциях x₁(t),…, x_p(t) и числах c₁,…, c_n.

Система с нелинейным оператором называется нелинейной. Принцип суперпозиции значительно облегчает исследования линейных систем в сравнении с нелинейными. При этом даже нелинейные системы стараются приближенно рассматривать как линейные. В результате возникли разные методы линеаризации нелинейных систем, т. е. приближенной замены нелинейных систем практически линейными.

Принцип суперпозиции дает возможность выразить реакцию линейной системы на любые воздействия через ее реакцию на определенный вид элементарных воздействий. Для этого необходимо разложить произвольное воздействие x(t) на элементарные воздействия выбранного типа. Зная реакцию линейной системы на элементарные воздействия, можно при помощи принципа суперпозиции определить ее реакцию на произвольные воздействия x(t). Таким образом, для определения реакции линейной системы на произвольное воздействия достаточно знать ее реакцию на выбранный стандартный тип элементарных воздействия. Тогда любая линейная система полностью характеризуется ее реакцией на какой-нибудь стандартный тип воздействий. В зависимости от выбора стандартного типа воздействий мы получим разные характеристики линейной системы.

Уравнения, описывающие поведение линейной системы, всегда линейны. Если все уравнения, описывающие поведение системы, линейны, то и сама система линейная. Если среди уравнений, которые описывают поведение элементов системы управления, имеется хотя бы одно нелинейное, то такая система является нелинейной.