1.5.6. Интегральные оценки качества

Интегральные оценки определяют путем интегрирования функций координат системы и их производных во времени. В автоматическом управлении получили распространение оценки с бесконечным верхним пределом интегрирования. Для таких оценок необходимо, чтобы подынтегральная функция со временем исчезала и не содержала, например, установившейся ошибки.

Простейшей интегральной оценкой может служить величина

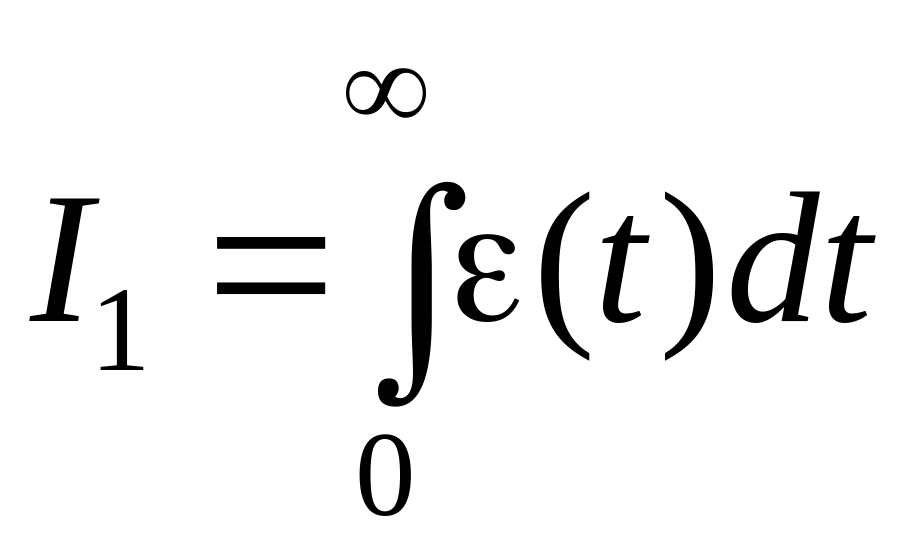, (1.248)

где (t)  отклонение регулируемой переменной от нового установившегося значения после завершения переходного процесса. Чем быстрее затухает переходный процесс и чем меньше отклонение регулируемой переменной от нового установившегося значения выходной переменной, тем меньше будет I₁.

Для вычисления интеграла (1.249) можно использовать выражение Лапласа от переменной (t):

.

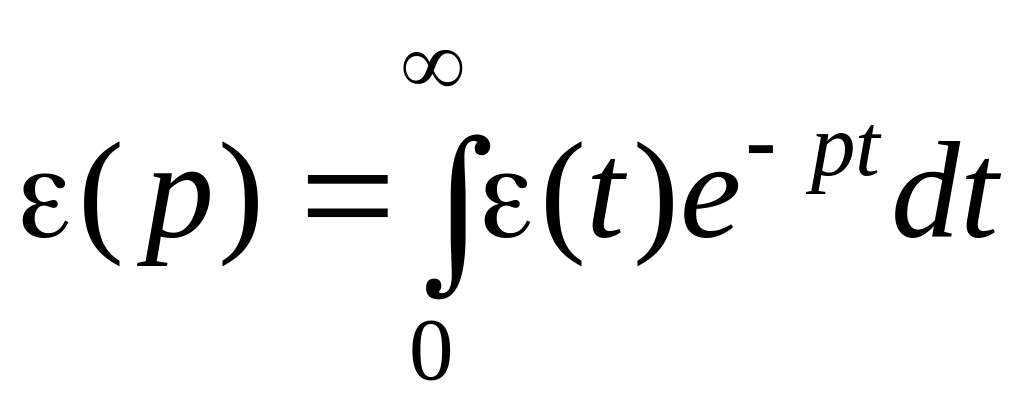Тогда I₁ можно найти посредством предельного перехода p  0:

. (1.249)

Такая оценка удобна при условии, что в системе наблюдаются монотонные переходные процессы и (t) не меняет знак. В противном случае используется квадратичная интегральная оценка:

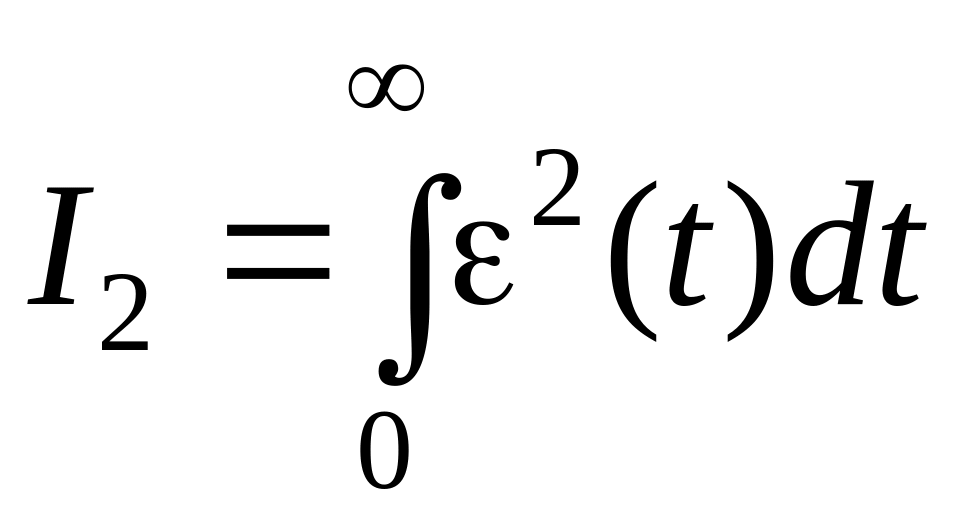. (1.250)

Такая оценка не зависит от знака ошибки отклонения и является достаточно универсальной.

Если передаточная функция системы имеет вид

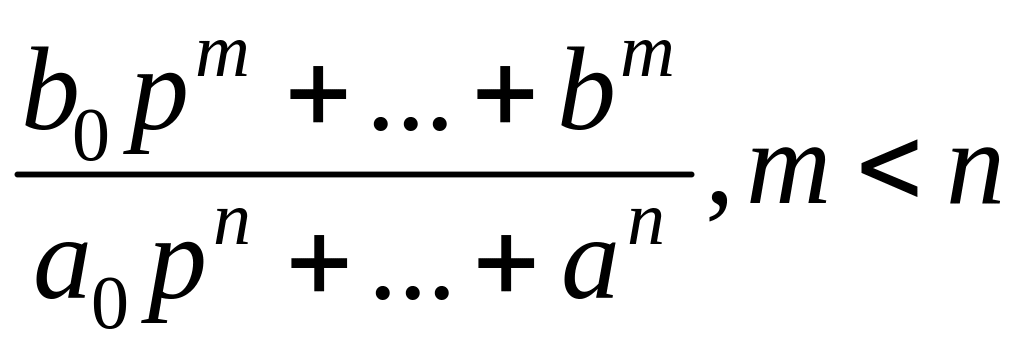, (1.251)

то можно воспользоваться формулами для вычисления I₂, которые предложены в работах А.А. Красовского При выполнении условий устойчивости квадратичная оценка для переменной y(t) выглядит следующим образом:

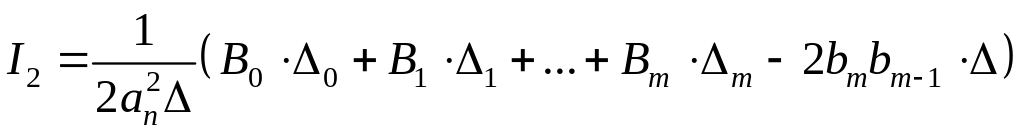, (1.252)

где

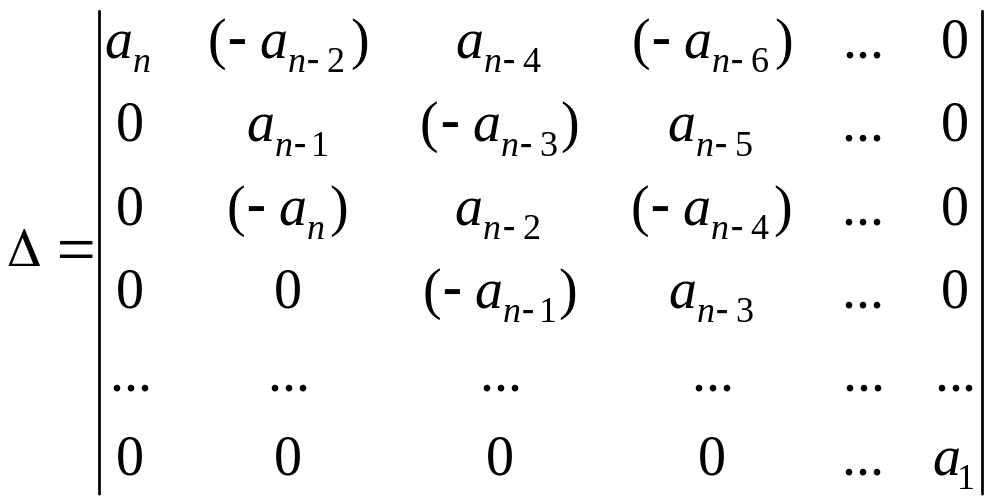, (1.253)

,

,

…,

,

,

_,  = 0, 1, …, m − определители, которые составляются из  заменой ( + 1)-го столбца столбцом a_n1, a_n, 0, …, 0.

Если же m = n и b_m = 0, то для этого случая

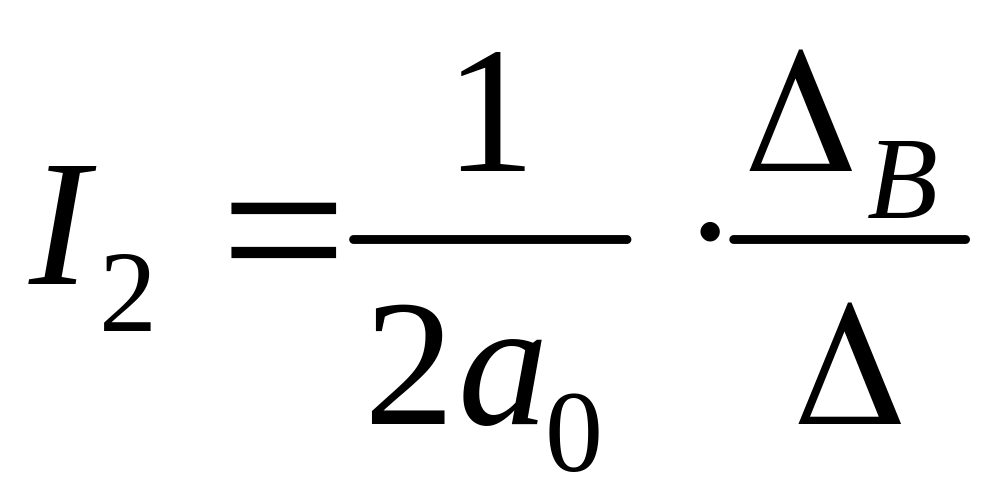, (1.254)

где _B получается из определителя  заменой нижней строки строкой B₁, …, B_n.

Если стремиться минимизировать интегральные показатели, то это требует энергичных воздействий на систему, что приводит к существенной величине перерегулирования. Для оценки склонности системы к существенному перерегулированию в состав подынтегральной функции вводится производная от квадрата ошибки:

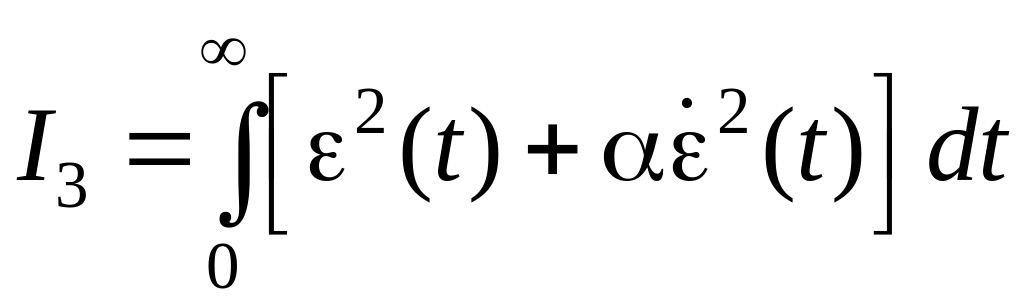, (1.255)

где −производная ошибки;  − весовой коэффициент.

1.5.7. Оценка качества систем управления при случайных возмущениях

Действующие в автоматических системах случайные возмущения обычно накладываются на полезные сигналы. При анализе точности автоматических систем обычно учитывается только случайность ошибок измерений, шумов и всех других помех, а полезные сигналы считаются определенными функциями времени. При таких условиях математические ожидания входных случайных функций обычно представляют собой полезные входные сигналы. Случайные колебания входных переменных около их математического ожидания, которые обычно называются флуктуациями входных переменных, представляют собой помехи, нарушающие нормальную работу системы и приводящие к случайным ошибкам в выходных переменных.

Разности между фактическими полезными сигналами системы и требуемыми входными сигналами представляют собой систематические ошибки системы. Случайные колебания выходных переменных представляют собой случайные ошибки системы.

Задача исследования точности автоматической системы состоит в определении ее систематических ошибок и вероятностных характеристик случайных ошибок, т. е. элементов рассеивания выходных переменных. При этом бывает достаточным определить дисперсии выходных переменных. Для нахождения систематических ошибок необходимо определить математическое ожидание ее выходных переменных.

Если известна весовая функция линейной системы q(t, ) и математическое ожидание входного сигнала m_x(t), то математическое ожидание выходного сигнала m_y(t) определяется как

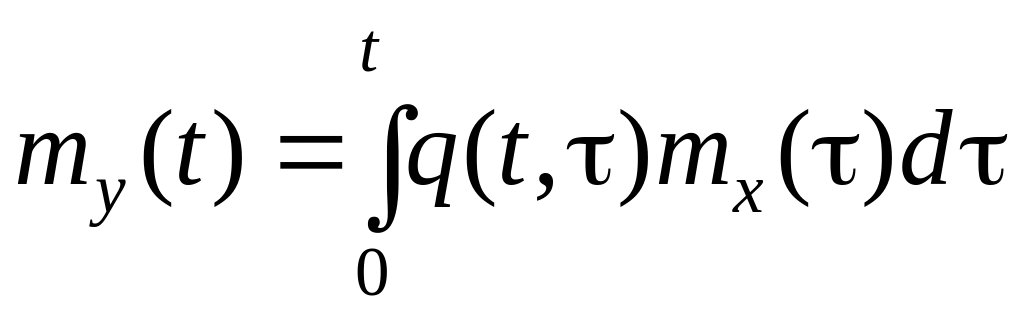. (1.256)

Корреляционная функция выходной переменной R_y(t, t') связана с корреляционной функцией входной переменной R_x(,') соотношением

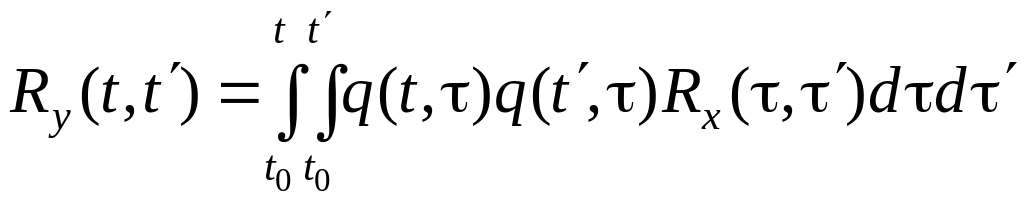. (1.257)

Для определения дисперсии выходной переменной положим t = t', и тогда

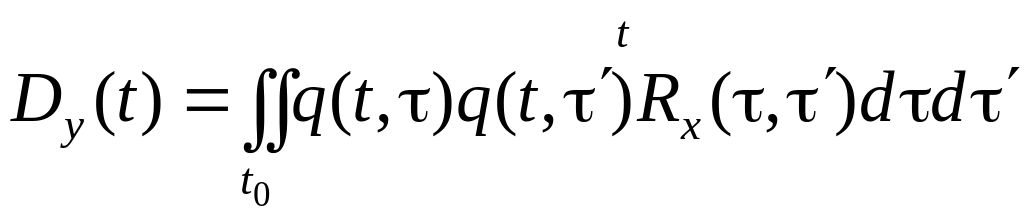. (1.258)

Таким образом, для оценки точности таких систем нужно знать математическое ожидание, корреляционную функцию входного сигнала и весовую функцию системы.

Для исследования точности линейных систем применяют также метод канонических представлений случайных функций. Если выразить входное случайное воздействие X(t) каноническим разложением

, (1.259)

где − интенсивности элементарных сигналов x_(t),

то на основании принципа суперпозиции выходная переменная выразится таким же каноническим разложением

, (1.260)

где функции m_y(t), y_(t) есть соответствующие результаты преобразований рассматриваемой системой входных переменных m_x(t) и x_(t).

Так,

,

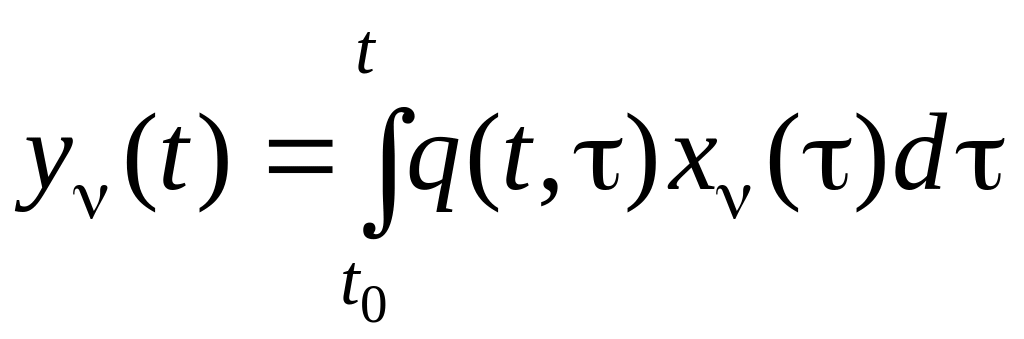а корреляционная функция выходной переменной Y(t) определяется как

. (1.261)

Отсюда дисперсия выходной переменной

. (1.262)