1.5. Качество процессов управления

Качество работы любой системы управления определяется величиной ошибки, равной разности между требуемым и действительным значениями регулируемой переменной. Знание мгновенных значений ошибки в течение всего времени работы объекта управления позволяет наиболее полно судить о свойствах системы управления. Однако для сравнения систем целесообразно подразделять некоторые их свойства на типовые воздействия. В этом случае для оценки качественных показателей используют критерии качества. Причем значимость критериев качества для разных систем определяется технологическими требованиями. Среди требований, предъявляемых к системам, можно выделить следующие: точность, быстродействие (производительность), запас устойчивости (степень удаленности системы от границы устойчивости) и обобщенные, или комплексные, показатели.

В качестве типовых входных воздействий для большинства практических задач исследования свойств систем используют единичный скачок, единичный сигнал постоянной скорости или гармонический сигнал. На основании таких исследований определяют так называемые прямые показатели качества. Оценки, полученные другими путями, называют косвенными.

1.5.1. Определение показателей качества по переходной характеристике

В качестве типового входного воздействия обычно используют единичный скачок. Пусть переходной процесс системы на это воздействие имеет вид, представленный на рис. 1.18.

Система склонна к колебаниям, следовательно, запас устойчивости можно охарактеризовать максимальным значением выходного параметра Y_max. Этот параметр хорошо согласуется с максимальными выбросами технологических параметров. Для оценки систем управления на основании данного параметра используется так называемое перерегулирование:

, (1.207)

где Y_ − установившееся значение выходного параметра на единичное воздействие.

В большинстве случаев считается, что запас устойчивости, является достаточным, если величина перерегулирования не превышает 10−30%. Бывают технологические процессы, для которых требуется, чтобы переходной процесс протекал монотонно, без перерегулирования.

Быстродействие системы можно определить по длительности переходного процесса t_п.

Y

Y_∞ = Y_жел

t_п

t

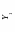
Рис. 1.18. Переходная характеристика системы

Длительность переходного процесса определяется как время от момента приложения на входе системы единичного скачка до того момента, когда начнет выполняться условие

, (1.208)

где  − заданная допустимая ошибка.

Степень затухания переходного процесса определяется соотношением

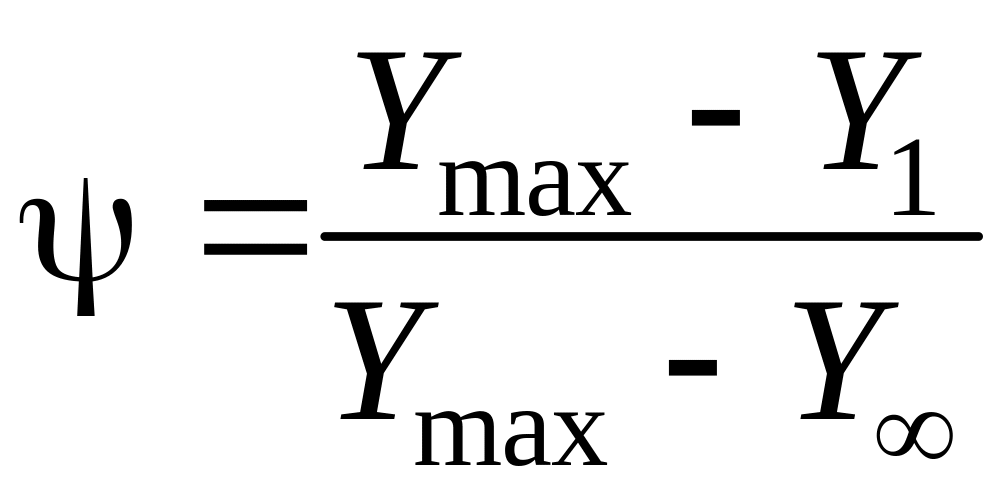. (1.209)

Колебательность системы характеризуется числом колебаний регулируемой величины за время переходного процесса t_п. Если за это время переходный процесс в системе совершает число колебаний меньше заданного по условиям технологии, то считается, что система имеет требуемое качество регулирования в части ее колебательности.

Установившаяся ошибка _ определяется как разность между установившимся значением регулируемой величины после окончания переходного процесса и ее заданным значением Y_жел:

_ = Y_жел  Y_. (1.210)

Для исследования реакции линейных детерминированных систем на типовые и произвольной формы воздействия в пакете MatLab предусмотрены специальные функции.

При исследовании реакции систем на входной ступенчатый сигнал используется функция «step».

Для оценки реакции системы на импульсный сигнал используется функция «impulse».

Если известен вид входного сигнала, который отличается от типовых, и необходимо оценить реакцию системы для таких условий, то применяется функция «isim».

Рассмотрим использование названных функций для нахождения реакции системы, имеющей передаточную функцию:

.

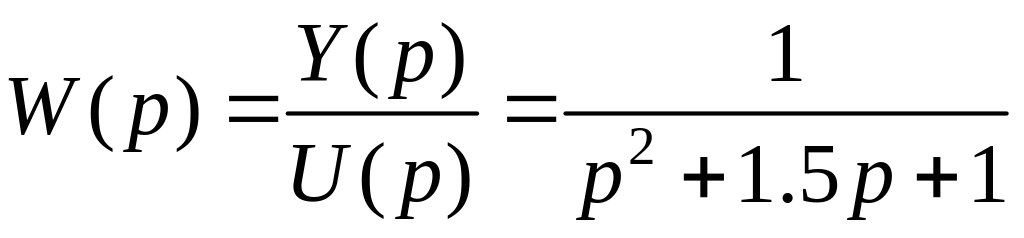Скрипты MATLAB для указанных воздействий:

1. num = [1]; den = [1 1.5 1];

sys = tf(num,den)

t = [0:0.1:12]

[y,t] = step(sys,t)

plot(t,y),grid

xlabel(‘время(сек)’)

ylabel(‘y(t)’)

2. num = [1]; den = [1 1.5 1];

sys = tf(num,den)

t = [0:0.1:12]

[y,t] = impulse(sys,t)

plot(t,y),grid

xlabel(‘время(сек)’)

ylabel(‘y(t)’)

3. num = [1]; den = [1 1.5 1];

sys = tf(num,den)

t = [0:0.1:12]

v1 = [0:0.1:6]; v2 = [6:-0.1:0]

u = [v1,v2]

[y,t] = isim(sys,t)

plot(t,y),grid

xlabel(‘время(сек)’)

ylabel(‘y(t)’)

В более общем случае можно рассмотреть описание вынужденных процессов в системе относительно внешнего воздействия f().

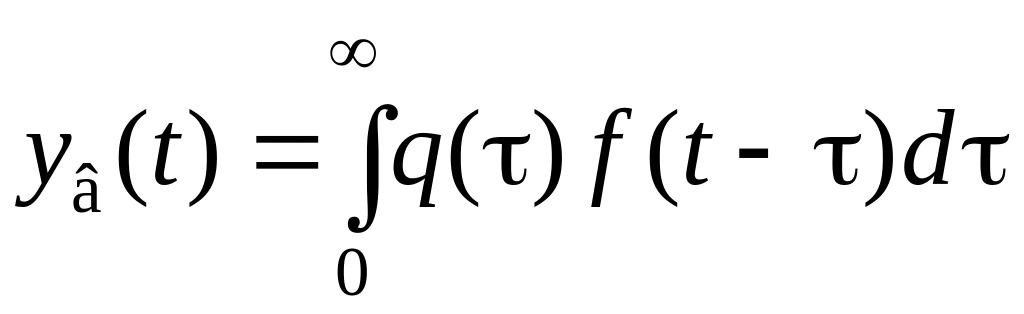. (1.211)

Если разложить f(t  ) в ряд Тейлора относительно t, то запишем

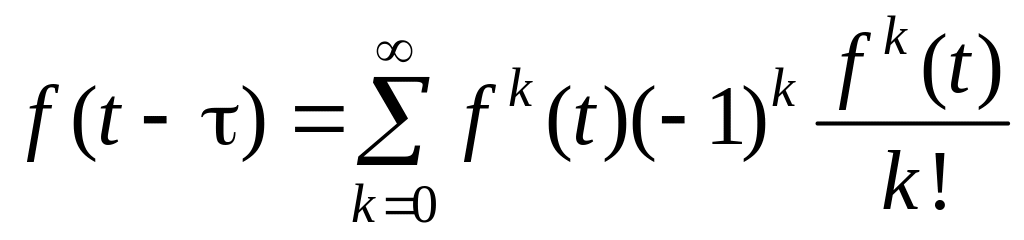. (1.212)

Подставив (1.213) в (1.212), получим

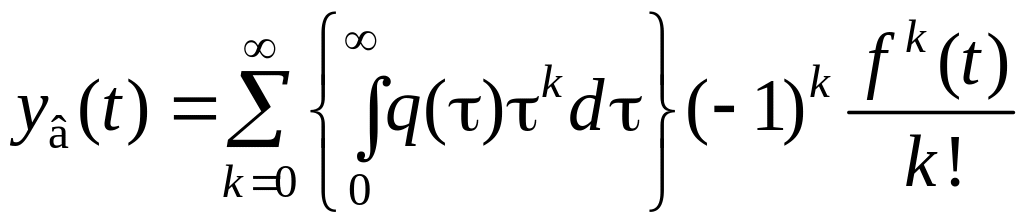, (1.213)

Обозначим выражение

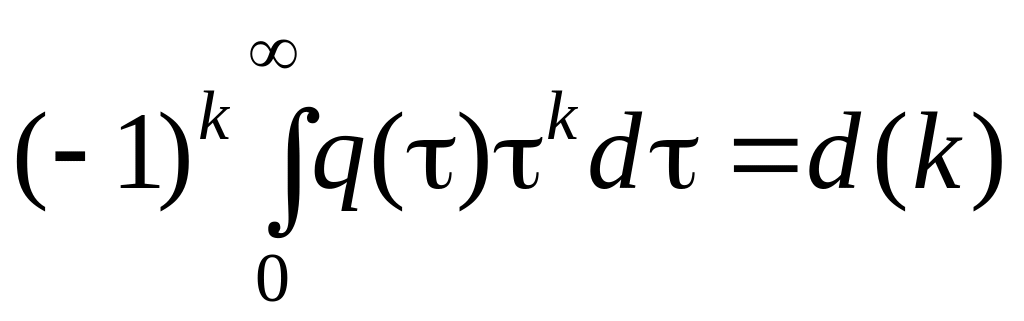, (1.214)

которое представляет моменты k-го порядка весовой функции. С учетом (1.214) перепишем (1.213):

. (1.215)

Вынужденные процессы в системе можно определить на основе моментов и производных от внешнего воздействия. Моменты d(k) можно определить на основе передаточной функции системы, которая связана с весовой функцией

.

Путем дифференцирования этого выражения по p k раз получим

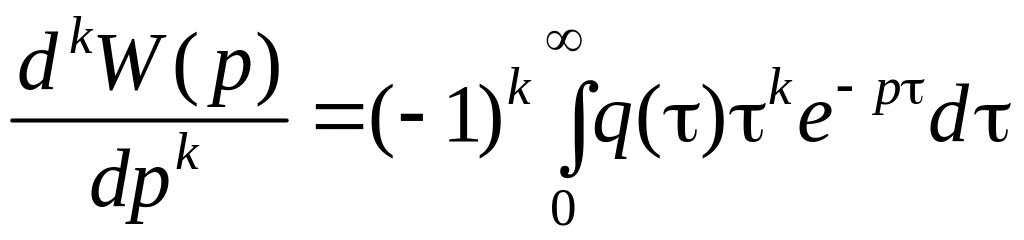. (1.216)

Устремляя p к нулю, найдем

. (1.217)

Если разложить W(p) в ряд по степеням, то получим

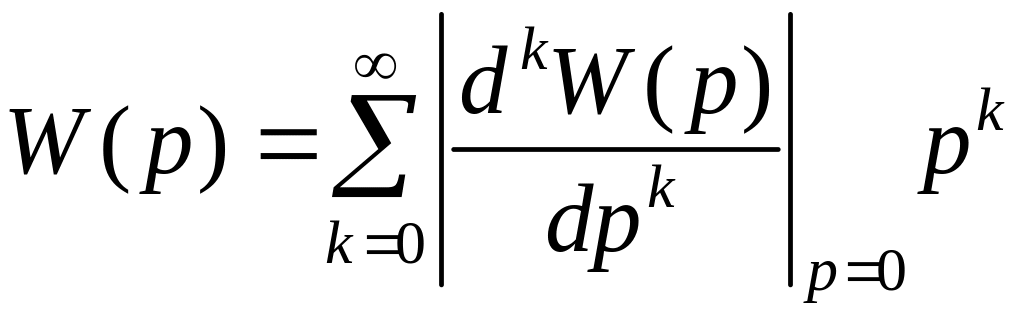, (1.218)

или

. (1.219)

Это позволяет определить d(k) путем деления многочлена числителя передаточной функции на многочлен знаменателя.

Если воздействие f(t) можно описать полиномом, то решение (1.214) имеет конечную сумму.