Глава 1. Анализ линейных непрерывных систем

1.1. Математическое описание сигналов

1.1.1. Понятие сигнала

В широком смысле под сигналом понимают материальный носитель информации. К сигналам относят как естественные сигналы, так и сигналы, специально создаваемые с определенной формой. Материальную основу сигнала составляет какой-либо физический объект или процесс, называемый носителем информации. Носитель становится сигналом в процессе модуляции.

В качестве носителей информации используются колебания различной формы, чаще всего гармонические, включая частный случай –постоянное состояние.

В носителе U(t) = const имеется только один параметр –напряжение. При использовании гармонических колебаний, носителями информации становятся такие параметры, как амплитуда, частота, фаза.

Сигналы принято подразделять на детерминированные и случайные. Детерминированными называют сигналы, параметры которых определены точно в любые моменты времени. Случайные отличаются тем, что значения их некоторых параметров предсказать невозможно. Они могут рассматриваться как случайные сигналы, когда несут полезную информацию, или как помехи, когда мешают наблюдению интересующих нас сигналов и управлению системой.

При изучении свойств сигналов и помех мы отвлекаемся от их конкретной физической природы, содержания и назначения, заменяя моделями. Модель – это выбранный способ описания объекта, процесса или явления, отражающий существенные с точки зрения решаемой задачи факторы.

В зависимости от структуры информационных параметров детерминированные сигналы подразделяют на непрерывные, дискретные и дискретно-непрерывные. Если множество возможных значений параметра сигнала образует континиум, то сигнал считают непрерывным по данному параметру. Сигнал считают дискретным по данному параметру, если число значений, которое может принимать этот параметр, конечно (или счетное). Сигнал, дискретный по одному параметру и непрерывный по другому, называют дискретно-непрерывным. В соответствии с этим существуют разновидности математического представления детерминированных сигналов.

1.1.2. Формы представления непрерывных детерминированных сигналов

Представим множество точек непрерывного сигнала в виде графика функции, зависящей от времени. Такая форма представления предназначена в первую очередь для анализа сигналов. Желательно найти такое представление сигнала, которое облегчает задачи исследования прохождения реальных сигналов, часто имеющих достаточно сложную форму, через интересующие нас системы. С этой целью сложные сигналы представляются совокупностью элементарных (базисных) функций, удобных для последующего анализа.

Наиболее широкий класс исследуемых систем – это инвариантные во времени линейные системы. При анализе прохождения сложного сигнала U(t) через такие системы его представляют в виде взвешенной суммы базисных функций φ_k(t) (или соответствующего интеграла)

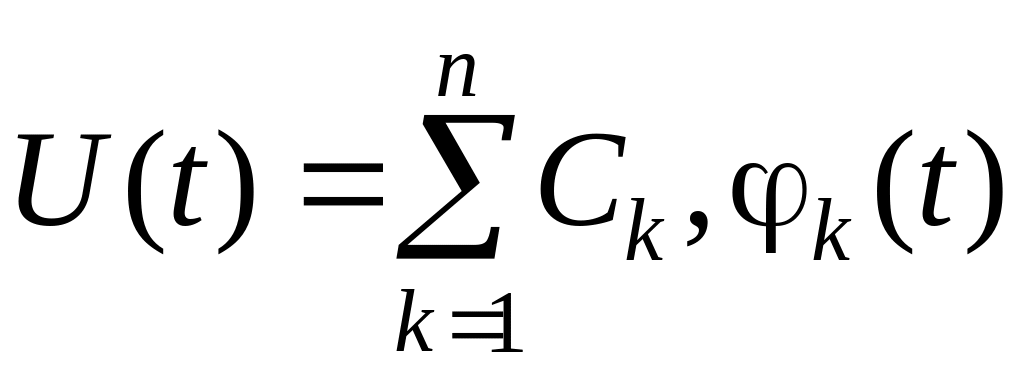, tt_, t_, (1.1)

где С_k – коэффициенты; t_, t_ – интервал существования сигнала. На интервале t_, t_ выражение справедливо как для сигналов, неограниченных во времени, так и для сигналов конечной длительности. Однако за пределами интервала t_, t_ сигнал конечной длительности не равен нулю, так как он представляется суммой в том случае, если условно считается периодически продолжающимся.

Вычисление составляющих сигнала существенно облегчается при выборе в качестве базиса системы функций ₀(t), ₁(t),…, _k(t),…, _j(t),…, _n, которую называют ортогональной на отрезке t_, t_ для всех , если удовлетворяются условия

при k  j, (1.2)

и ортонормированной, если

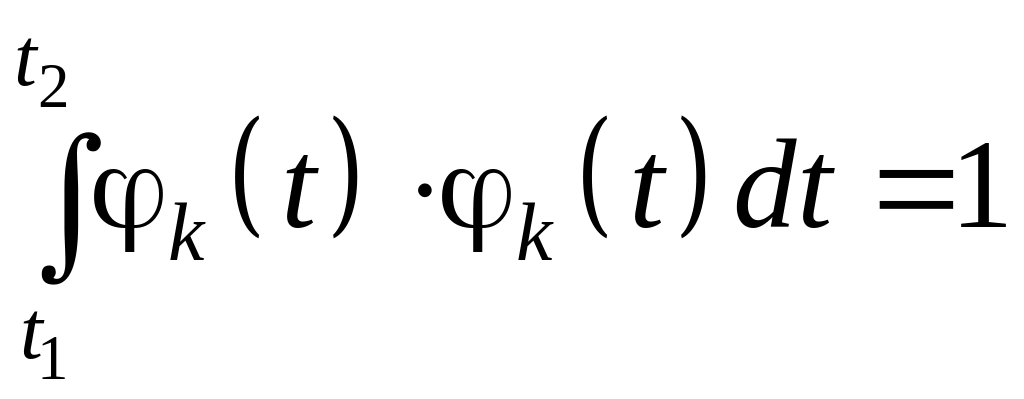при k = j. (1.3)

Широко известной ортонормированной системой является совокупность тригонометрических функций кратных аргументов: 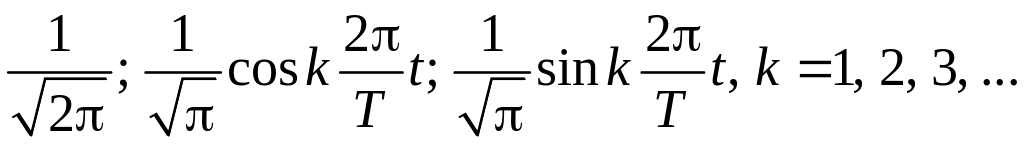Она ортонормальна на отрезке [, ]. Такое разложение исторически появилось первым и было названо рядом Фурье. Известны представления сигналов по системам ортогональных базисных многочленов Чебышева, Лагера, Лежандра.

Распространенной временной формой представления сигнала является такое разложение сигнала U(t), при котором в качестве базисной функции используются единичные импульсные функции – дельта-функции.

Математическое описание такой функции задается соотношениями:

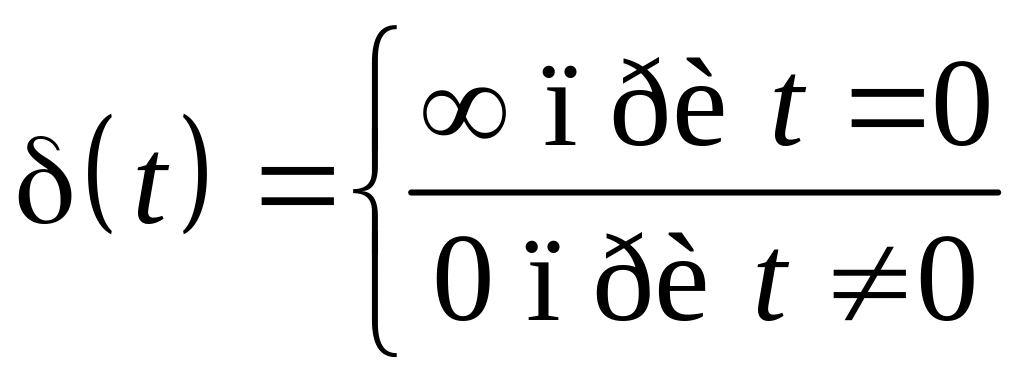; (1.4)

.

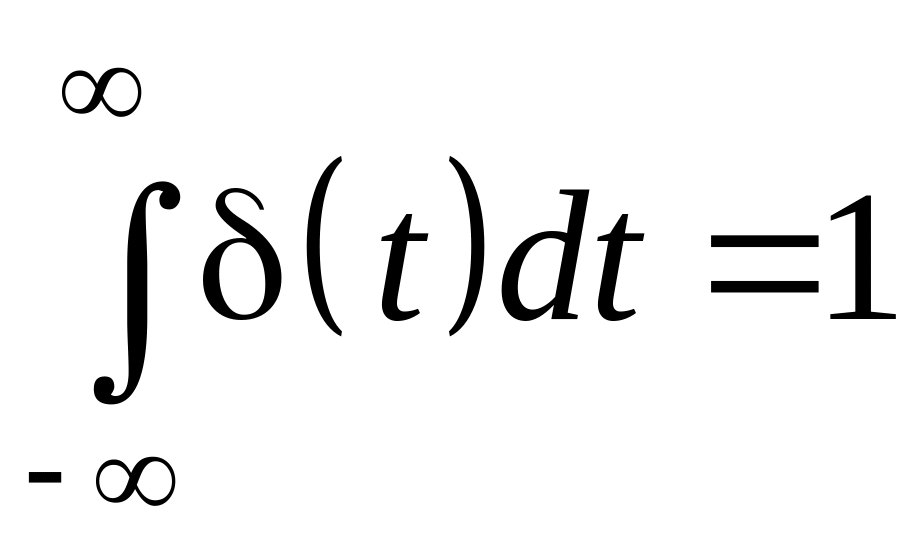Для более общего случая, когда дельта-функция отличается от нуля в момент времени t = , имеем:

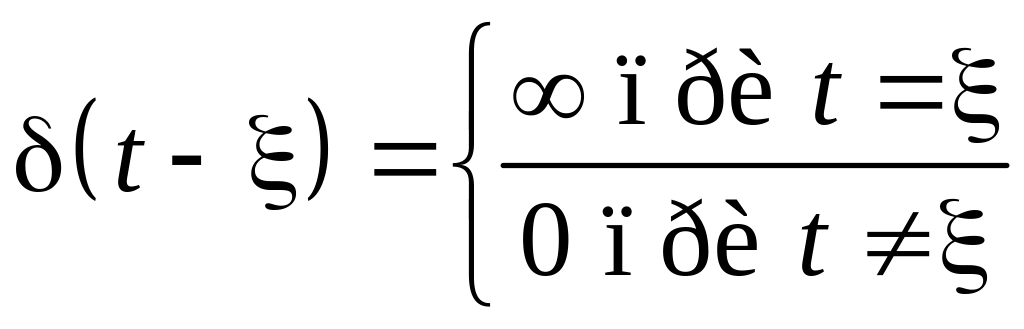; (1.5)

.

Такая математическая модель соответствует абстрактному импульсу бесконечно малой длительности и безграничной величины. Единственным параметром, который правильно отражает реальный сигнал, является время. Однако, учитывая (1.5), с помощью дельта-функции можно выразить значение реального сигнала U(t) в конкретный момент времени :

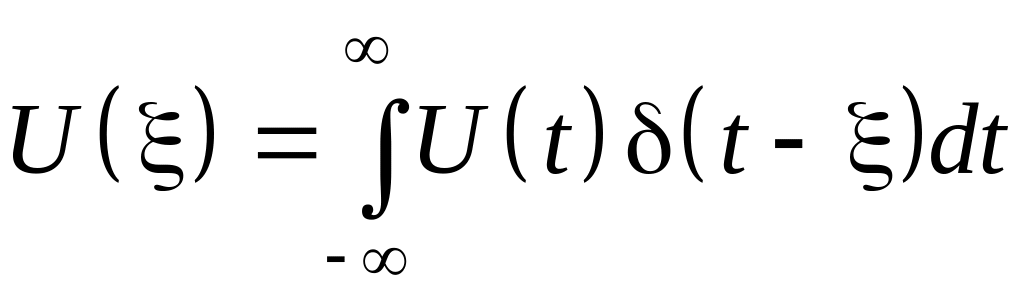. (1.6)

Равенство (1.6) справедливо для любого текущего момента времени t.

Заменив  на t и приняв в качестве переменной интегрирования , получим

. (1.7)

Таким образом, функция U(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Ортогональность совокупности таких импульсов очевидна, так как они не перекрываются во времени.

Формула (1.7) справедлива и для более узкого диапазона пределов интегрирования. Так, для любого  > 0 имеем

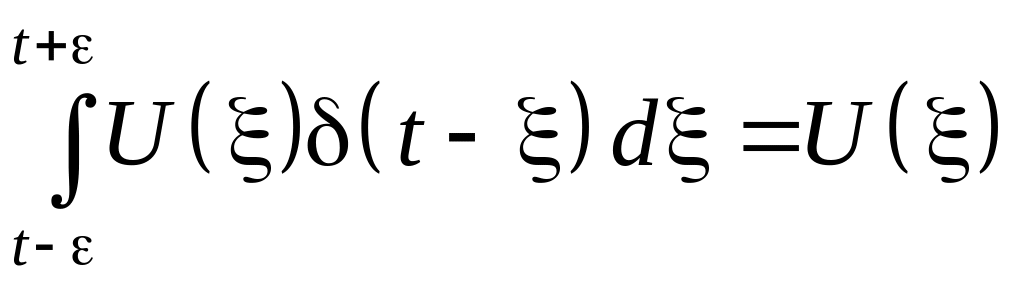. (1.8)

В практических приложениях бывает удобно пользоваться также производными импульсной -функции. Применяя производные -функций, мы можем формально дифференцировать равенства (1.7)−(1.8), являющиеся тождествами относительно t при изменении t в интервале [t₁, t₂].

При условии, что U(t) имеет непрерывные производные до n-го порядка, с учетом производных -функции имеем

(1.9)

и аналогично

(1.10)

при k = 1, 2,…, n.

Единичную импульсную -функцию можно представить прямоугольным импульсом конечной длительности Δ, имеющим единичную площадь в виде рис. 1. Тогда можно записать, что

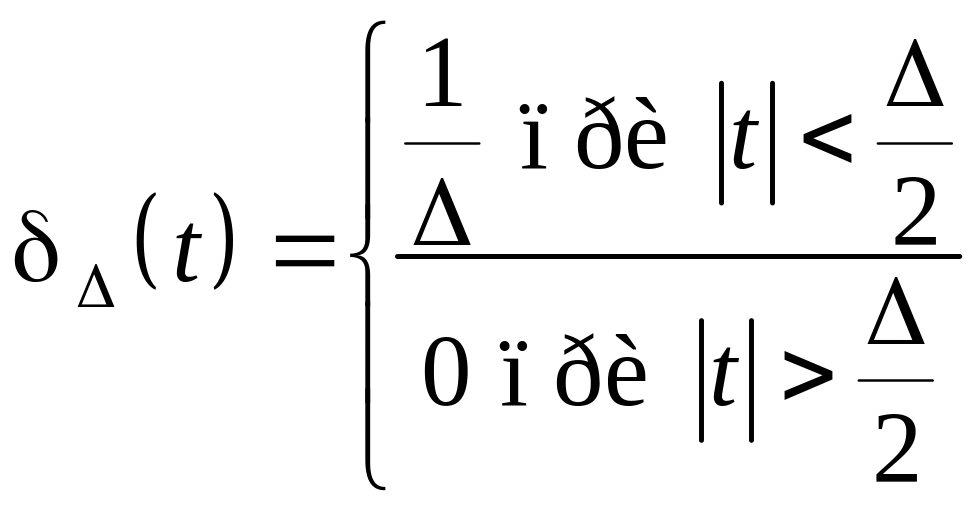. (1.11)

Представим интегралом Фурье единичный прямоугольный импульс _(t), определяемый формулой (1.11).

Из анализа известно, что любая абсолютная интегрируемая функция f(t) (т.е. такая функция, интеграл от абсолютной величины которой в бесконечных пределах имеет конечное значение) может быть представлена интегралом Фурье

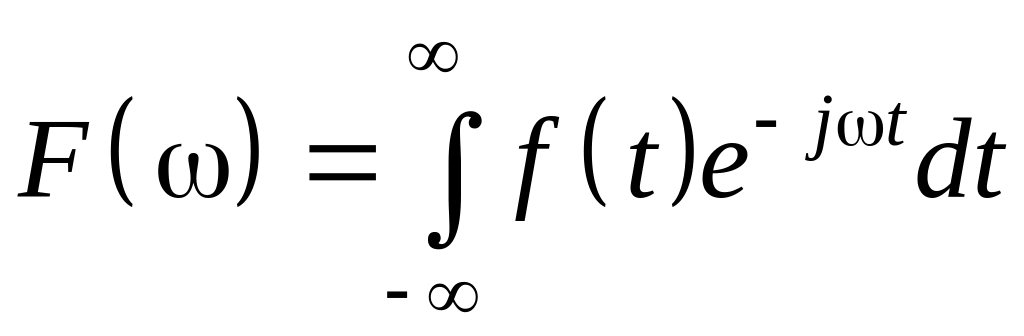(1.12)

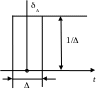
Pис.1.1. Графическая интерпретация функции Дирака

Подставляя в (1.14) выражение (1.13) прямоугольного импульса, будем иметь

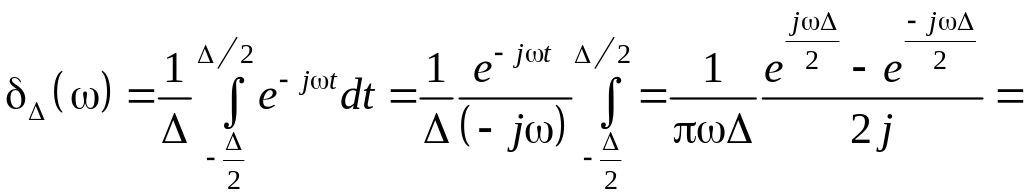
(1.13)

Выполнив обратное преобразование Фурье для (1.15), получим

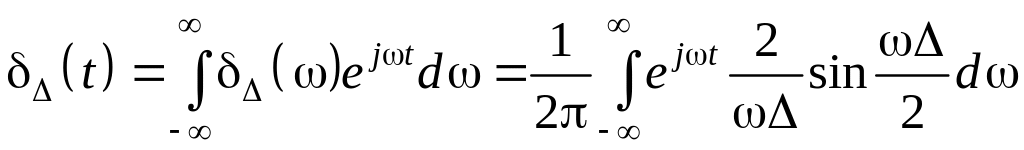. (1.14)

Переходя к пределу при Δ→0 и принимая во внимание, что при этом , получим

. (1.15)

Эта формула дает разложение мгновенного единичного импульса на гармонические колебания всех возможных частот.

Можно подставить выражение (1.17) в формулу (1.7), что позволяет сказать о возможности использования экспоненциальных функций в качестве базисных для сигнала системы.

Использование экспоненциальных базисных функций в преобразовании Фурье комплексно-сопряженными парами (с положительным и отрицательным параметром ) позволяет в соответствии с формулой Эйлера

(1.16)

представить сложный детерминированный сигнал в виде суммы гармонических составляющих. Поскольку параметр  в этом случае имеет смысл круговой частоты, результат такого преобразования называют частотной формой представления сигнала.