
- •24. Предмет математической статистики. Генеральная и выборочная совокупности. Статистический ряд распределения выборки. Полигон и гистограмма. Эмпирическая функция распределения.
- •27. Точечные и интервальные оценки параметров распределения. Доверительная вероятность (надёжность) и доверительный интервал.
- •29. Статистическая проверка гипотез (гипотеза, статистическая гипотеза, нулевая и конкурирующая гипотезы, ошибка первого и второго рода).
- •31. Проверка гипотезы о нормальном распределении генеральной совокупности с помощью критерия Пирсона 2 (хи – квадрат).
- •25. Статистические оценки параметров распределения.
- •32.Понятие корреляционной зависимости. Корреляционная таблица.
- •33.Эмпирическая линия регрессии. Линейная корреляция. Коэффициент корреляции. Свойства коэффициента корреляции.
- •34.Метод наименьших квадратов для определения параметров линейной регрессии. Коэффициент детерминации, доверительный интервал для коэффициента корреляции генеральной совокупности.
- •35.Основные понятия дисперсионного анализа. Однофакторный дисперсионный анализ.
- •36.Двухфакторный дисперсионный анализ.
35.Основные понятия дисперсионного анализа. Однофакторный дисперсионный анализ.
Дисперсионный анализ – анализ изменчивости признака под влиянием каких-либо контролируемых переменных факторов.
Однофакторный дисперсионный анализ используется в тех случаях, когда есть в распоряжении три или более независимые выборки, полученные из одной генеральной совокупности путем изменения какого-либо независимого фактора, для которого по каким-либо причинам нет количественных измерений.
Пусть
результаты наблюдений составляют l
независимых выборок (групп), полученных
из нормальных совокупностей , которые
имеют, вообще говоря, различные средние
значения a1,a2,…,al
и равные
дисперсии
![]() .Соответственно
объемы выборок n1,
n2,
…, nl,
.Соответственно
объемы выборок n1,
n2,
…, nl,
![]() -
общее число наблюдений. Проверяется
гипотеза Н0:
a1=a2=…=al.
-
общее число наблюдений. Проверяется
гипотеза Н0:
a1=a2=…=al.
Для l = 2 используются рассмотренные ранее критерии значимости.
Если l > 2, то для проверки гипотезы о равенстве l средних применяют однофакторный дисперсионный аналіз.
Суть однофакторного дисперсионного анализа заключается в следующем:
обозначим
xik
- i-й элемент
k-ой выборки
![]() ,
,
![]() ,
,
![]() -
выборочное среднее k-ой выборки ,
-
выборочное среднее k-ой выборки ,
![]() ,
,
![]() -
общее выборочное среднее,
-
общее выборочное среднее,
![]() .
.
Основное тождество дисперсионного анализа записывается так:
![]()
Запишем его в виде:
Q= Q1+Q2 ,
где Q- общая сумма квадратов отклонений наблюдений от общего среднего,
Q1- сумма квадратов отклонений выборочных средних от общего среднего,
Q2- сумма квадратов отклонений наблюдений от групповых средних,
Q 0 , Q1 0, Q2 0
Рассматривается
статистика
![]() ,
,
имеет распределение Фишера с (l-1)(n-l) степенями свободы.
Если
выполняется неравенство
![]() ,
,
то
Н0 гипотеза
принимается на уровне значимости
![]() .
.
36.Двухфакторный дисперсионный анализ.
Одной из используемых моделей данных в дисперсионном анализе является двухфакторная модель. Она состоит в учёте систематических и случайных ошибок в определении измеряемых параметров.
Пусть
с помощью методов ![]() производится
измерение нескольких параметров, чьи
точные значения —
производится
измерение нескольких параметров, чьи
точные значения — ![]() .
В таком случае, результаты измерений
различных величин различными методами
можно представить как:
.
В таком случае, результаты измерений
различных величин различными методами
можно представить как:
![]() ,
,
где:
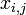 —
результат
измерения
—
результат
измерения 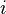 -го
параметра по методу
-го
параметра по методу 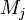 ;
;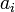 —
точное
значение
-го
параметра;
—
точное
значение
-го
параметра;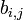 —
систематическая
ошибка измерения
-го
параметра по методу
;
—
систематическая
ошибка измерения
-го
параметра по методу
;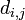 —
случайная
ошибка измерения
-го
параметра по методу
.
—
случайная
ошибка измерения
-го
параметра по методу
.
Тогда
дисперсии случайных величин
, ![]() ,
, ![]() ,
, ![]() (где:
(где:
![]()
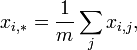
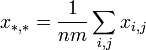 )
выражаются как:
)
выражаются как:
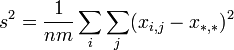
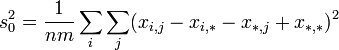
![]()
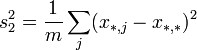
и удовлетворяют тождеству:
![]()
Двухфакторная схема позволяет лишь обнаружить систематические расхождения, но непригодна для их численной оценки с последующим исключением из результатов наблюдений. Эта цель может быть достигнута только при многократных измерениях.
1
Выборочное среднее, кроме того, можно
вычислить еще по формуле:
![]() где
где
![]()
2 Стьюдент (Student) [псевдоним Уильяма Сили Госсета (Gosset W.S., 1876–1937)] ― английский математик и статистик.
3 Пирсон Карл (Чарлз) [Pearson Karl (Cyarles), 1857–1936] ― английский математик, биолог и философ.
4
Например, для нормального распределения
― два параметра: математическое
ожидание
![]() и среднее квадратическое отклонение
и среднее квадратическое отклонение ![]()
![]()
