§ 7. Понятие о ранге матрицы

1. Миноры. В главе 1 читатель уже познакомился с понятием минора квадратной матрицы. Сейчас мы несколько обобщим это понятие.

Определение 7.1. Пусть – матрица размера и пусть . Если в матрице выбрать любые строк и столбцов, то элементы, расположенные на их пересечении, образуют определитель порядка . Всякий такой определитель, составленный из выбранных строк и столбцов матрицы , называется ее минором порядка .

Рассмотрим «крайние случаи» миноров. Условимся, что определитель квадратной матрицы порядка является ее минором порядка . Ясно, что – минор наибольшего порядка в матрице . В общем случае наибольший порядок минора равен минимуму числа срок и числа столбцов матрицы. Любой элемент матрицы является ее минором порядка 1 и представляет собой минор минимального порядка.

На практике удобнее оказывается не выделять выбранные строки и столбцы, а вычеркивать невыбранные.

Пример. Вычеркнув первый и третий столбцы и вторую строку приведенной ниже матрицы , получаем следующий ее минор порядка 3: .

Отметим, что всякий определитель порядка , полученный из данной матрицы вычеркиванием нескольких ее строк и нескольких ее столбцов, является минором порядка этой матрицы. Порядок минора равен числу его строк.

Уточним, что количество вычеркнутых строк произвольно и может принимать значения от до . В частности, может быть вычеркнута одна строка. В некоторых ситуациях для получения минора требуется вычеркнуть только столбцы. Аналогично, число вычеркнутых столбцов может принимать значения от до . Таким образом, миноры, рассмотренные в главе 2, являются с точки зрения этого определения минорами порядка .

Примеры.

1). , – миноры порядка 3 матрицы ;

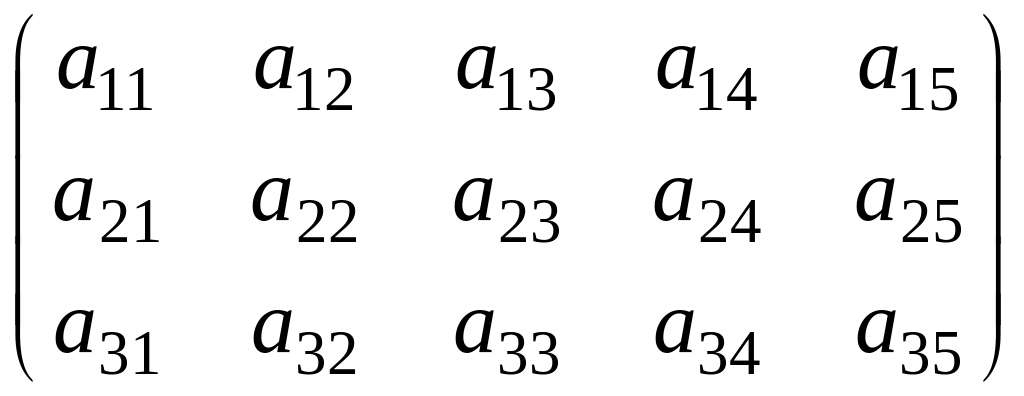2). , – миноры второго порядка этой матрицы;

3). – минор второго порядка матрицы ,

, , , – миноры первого порядка этой же матрицы.

2. Вычисление ранга матрицы. Для изучения дальнейшего материала требуется усвоить теорему 4.3, описывающую поведение определителей при элементарных преобразованиях строк, а также другие свойства определителей (см. §4).

Определение 7.2. Рангом матрицы называется наибольший порядок ее ненулевого минора. Ранг нулевой матрицы равен нулю.

Примеры.

1). Ранг матрицы равен двум, поскольку – ее ненулевой минор наибольшего порядка.

2). Ранг матрицы также равен двум. В самом деле, единственный минор третьего порядка равен нулю, так как имеет два одинаковых столбца, а минор второго порядка .

3). Ранг матрицы равен трем, поскольку она имеет ненулевой минор третьего порядка, а миноров четвертого порядка для этой матрицы вообще составить нельзя ввиду того, что она имеет только три строки.

Пусть и – миноры матрицы . Если минор содержится в миноре и порядок минора на единицу меньше порядка минора , то говорят, что окаймляет минор . Иначе говоря, минор окаймляет минор , если минор получается из минора вычеркиванием одной строки и одного столбца.

Примем без доказательства следующее правило.

Правило окаймляющих миноров. При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор ‑го порядка , отличный от нуля, то требуют вычисления лишь миноры ‑го порядка, окаймляющие минор : если все они равны нулю, то ранг матрицы равен

Задача 1. Вычислить ранг матрицы .

Решение. В левом верхнем углу расположен ненулевой минор порядка 2. Существуют только 2 минора порядка 3, окаймляющих данный: и 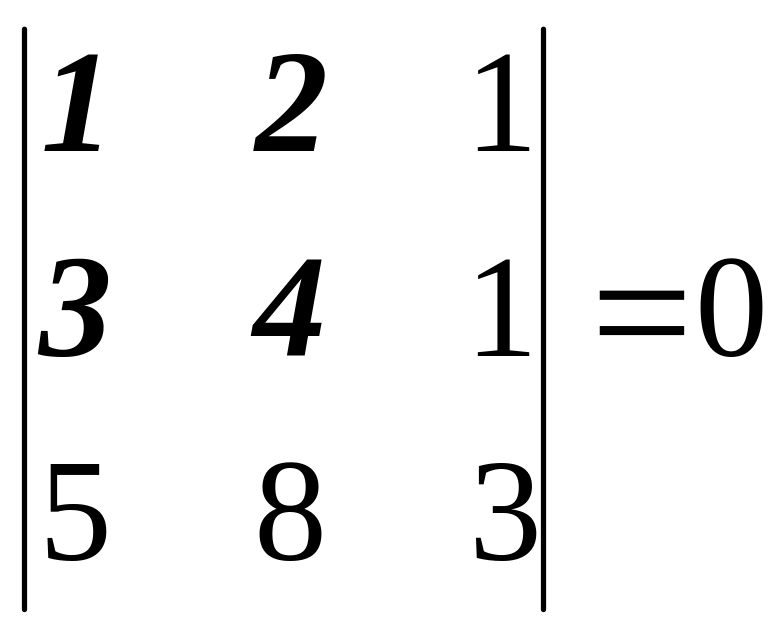, причем оба они равны нулю. Поэтому ранг матрицы равен 2.

Задача 2. Вычислить ранг матрицы .

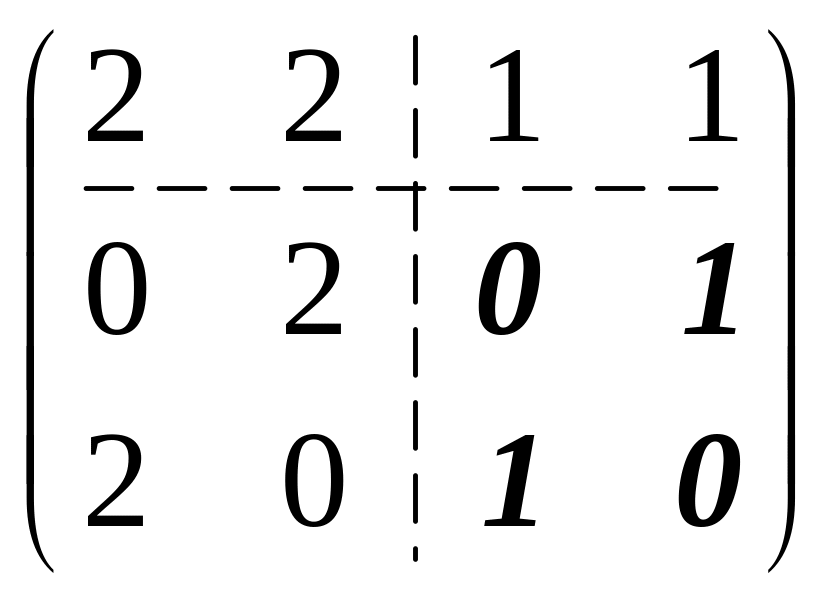Решение. В правом нижнем углу расположен ненулевой минор порядка 2. Любой минор, окаймляющий данный, равен нулю, так как содержит два пропорциональных столбца. Поэтому ранг матрицы равен 2.

Задача 3. Вычислить ранг матрицы .

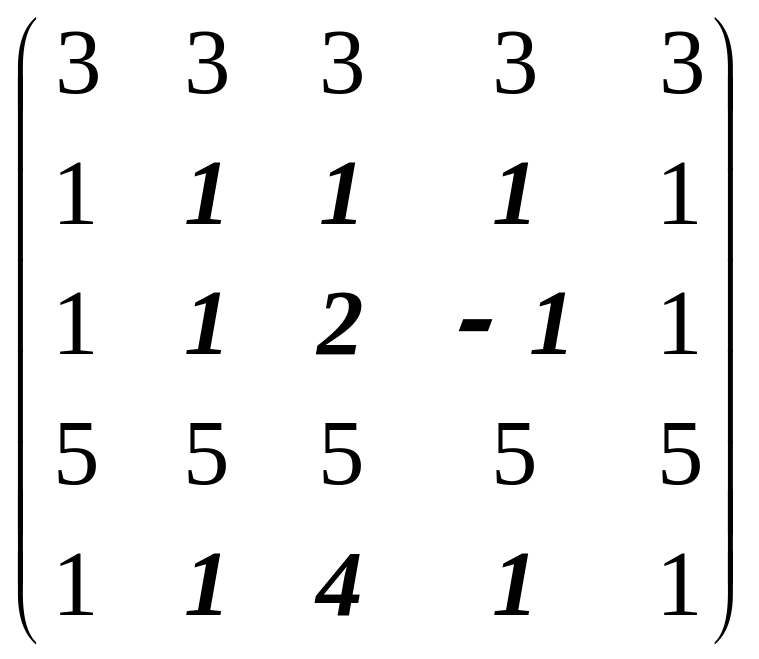Решение. На пересечении второго, третьего и четвертого столбцов со второй, третьей и пятой строками расположен не нулевой минор (определитель Вандермонда). Однако любой минор, окаймляющий этот определитель, равен нулю, так как содержит два одинаковых столбца. Поэтому ранг матрицы равен 3.

Далее мы докажем два свойства ранга матрицы, позволяющие эффективно его вычислять:

1) ранг не меняется при элементарных преобразованиях строк,

2) ранг ступенчатой матрицы равен числу его нулевых строк.

Лемма 7.3. Если матрица получена из матрицы с помощью одного элементарного преобразования строк, то .

Доказательство. Пусть . Тогда достаточно доказать, что всякий минор матрицы равен нулю, если его порядок больше, чем . Итак, всюду далее – произвольная квадратная подматрица матрицы , причем порядок больше, чем . Рассмотрим отдельно элементарные преобразования строк трех типов.

I). Если матрица получена из матрицы преобразованием строк первого типа, то подматрица либо совпадает с некоторой подматрицей матрицы , либо получается из перестановкой двух строк местами. В первом случае , а во втором , поскольку – минор матрицы порядка большего, чем .

II). Допустим теперь, что матрица получается из матрицы прибавлением к ‑ой строке матрицы ее ‑ой строки, умноженной на число . Тогда возможны три варианта взаимного расположения подматрицы и строк с номерами и :

1) ‑я и ‑я строки обе пересекают подматрицу ,

2) ‑я строка проходит через подматрицу , а ‑я строка не имеет с этой подматрицей общих элементов,

3) ни ‑я, ни ‑я строки не имеют общих элементов с подматрицей .

При первом варианте расположения подматрица получается из некоторой подматрицы матрицы прибавлением к одной строке подматрицы другой ее строки, умноженной на число, и, следовательно, . В случае второго варианта расположения минор разлагается в алгебраическую сумму двух миноров:

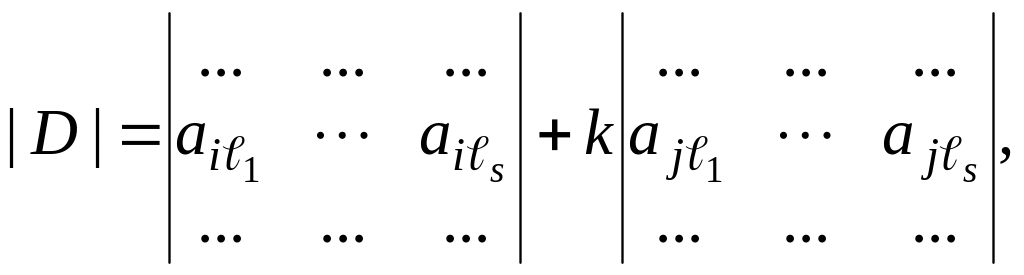
первый из которых является минором матрицы , а второй отличается от некоторого минора матрицы только перестановкой строк. Так как оба этих минора равны нулю, то .

И, наконец, если ни ‑я, ни ‑я строки не имеют общих элементов с подматрицей , то при переходе от матрицы к матрице соответствующая подматрица вообще никак не изменится. Значит, как минор в порядка большего, чем .

III). Пусть матрица получается из матрицы умножением ‑ой строки на ненулевое число . Тогда минор порядка большего, чем , равен нулю, так как он либо совпадает с некоторым минором матрицы , либо получается из минора умножением некоторой его строки на число  . 

Лемма 7.4. Если матрица получена из матрицы с помощью конечного числа элементарных преобразований строк, то .

Доказательство. Пусть матрица получена из матрицы с помощью конечного числа элементарных преобразований строк. Пусть – последовательность матриц, каждая из которых, начиная с , получена из предыдущей с помощью одного элементарного преобразования строк. Тогда в силу леммы 7.3 . Следовательно, . ■

Элементарные преобразования строк (см. определение 4.2), как показывает следующая лемма, являются обратимыми.

Лемма 7.5. Если матрица получена из матрицы с помощью одного элементарного преобразования строк, то и матрицу можно получить из матрицы с помощью одного элементарного преобразования строк.

Доказательство. 1). Пусть матрица получена из матрицы перестановкой двух строк местами. Тогда, поменяв местами в матрице строки с теми же номерами, получим матрицу .

2). Пусть матрица получена из матрицы прибавлением к ее ‑ой строке ее ‑ой строки, умноженной на число . Тогда матрица получается вычитанием из ‑ой строки матрицы ее ‑ой строки, умноженной на число  . Отметим, что такое вычитание – то же самое, что прибавление к ‑ой строке ‑ой строки, умноженной на число . Поэтому получается из с помощью элементарного преобразования строк II-го типа.

3). Пусть матрица получена из матрицы умножением ‑ой строки на ненулевое число . Тогда, умножив ‑ую строку матрицы на число , мы вновь получим матрицу . Лемма доказана. ■

Определение 7.6. Матрицы и называются строчно эквивалентными (обозначение ), если или матрица может быть получена из матрицы с помощью конечного числа элементарных преобразований строк.

Теорема 7.7. Если матрица получена из матрицы с помощью конечного числа элементарных преобразований строк, то и матрицу можно получить из матрицы с помощью конечного числа элементарных преобразований строк.

Доказательство. Пусть матрица получена из матрицы с помощью конечного числа элементарных преобразований строк. Пусть – последовательность матриц, каждая из которых, начиная с , получена из предыдущей с помощью одного элементарного преобразования строк. Тогда в силу леммы 7.5 в последовательности каждая матрица, начиная с , получается из предыдущей с помощью одного элементарного преобразования строк. ■

Теорема 7.7 показывает, что отношение строчной эквивалентности является симметричным. Легко видеть, что это отношение является рефлексивным и транзитивным.

Следующая теорема показывает, что ранг матрицы не меняется при элементарных преобразованиях строк.

Теорема 7.8. Если , то .

Доказательство. Пусть матрица получена из матрицы с помощью конечного числа элементарных преобразований строк. Тогда в силу леммы 7.4 .

По теореме 7.7 матрица получается из матрицы с помощью конечного числа элементарных преобразований строк. Отсюда по лемме 7.4 . Таким образом, . ■

Следствие 7.9. Ранг любой матрицы равен рангу ее ступенчатой формы.

Теорема 7.10. Ранг ступенчатой матрицы равен числу ее ненулевых строк.

Доказательство. Пусть ступенчатая матрица содержит ненулевых строк.

.

Рассмотрим подматрицу , расположенную на пересечении первых строк матрицы и ее ведущих столбцов:

.

На главной диагонали подматрицы расположены лидеры строк матрицы , поэтому эта подматрица является верхнетреугольной матрицей с ненулевыми элементами на главной диагонали. По свойству 7 (§4) определитель равен произведению элементов на главной диагонали и поэтому отличен от нуля. Следовательно, матрица имеет ненулевой минор порядка . По свойству 8 (§4) любой минор большего порядка равен нулю, так как содержит нулевую строку. Поэтому . ■

Следствие 7.9 и теорема 7.10 предоставляют практический метод определения ранга матрицы: элементарными преобразованиями строк приводят ее к ступенчатой форме и определяют число ненулевых строк последней.

Пример 7.11. 1). Найти ранг матрицы .

Ранг этой матрицы равен 2.

2). Найти ранг матрицы .

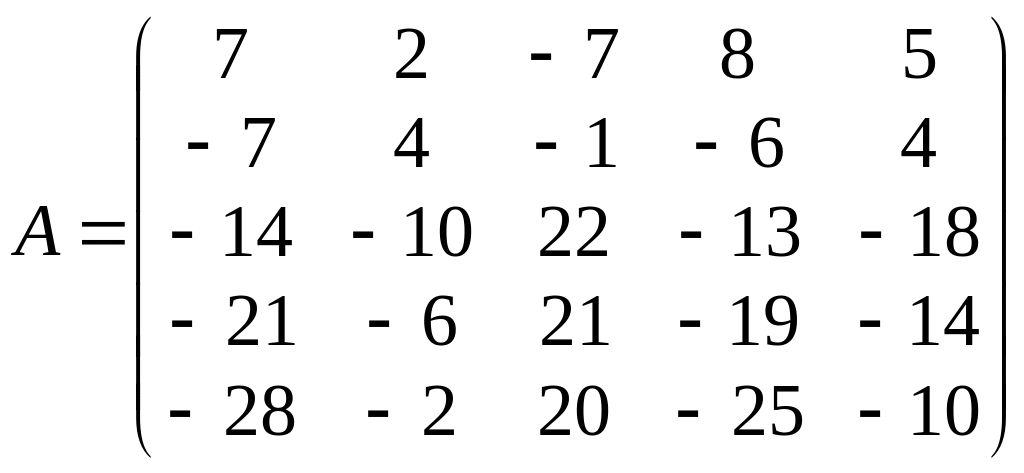Приведем матрицу к ступенчатой форме элементарными преобразованиями строк:

.

Матрица является ступенчатой и число ее ненулевых строк равно 3, поэтому ранг матрицы равен 3.

Замечание. Вообще говоря, элементарные преобразования строк нужно выполнять последовательно одно за другим. Однако последовательное выполнение преобразований II-го типа можно свести к одновременному их выполнению в том случае, если выбранная строка (называемая разрешающей) используется для изменения других строк матрицы, оставаясь при этом неизменной. Одновременное выполнение других комбинаций преобразований II типа может привести к матрице, не являющейся строчно эквивалентной данной. Так, например, если над матрицей одновременно, т. е. используя все время старые строки, совершить следующую комбинацию преобразований: , , , то получится матрица , не эквивалентная матрице , поскольку , а .

Лемма 7.12. .

Доказательство. В силу свойства равноправия строк и столбцов определителя любой минор матрицы совпадает с некоторым транспонированным минором матрицы , и наоборот. Так как при транспонировании определитель не меняет своего значения, то наибольшие порядки отличных от нуля миноров в матрицах и совпадают.  ■

По аналогии с элементарными преобразованиями строк можно определить элементарные преобразования столбцов матрицы.

Следствие 7.13. Ранг матрицы не изменится, если над матрицей совершить несколько элементарных преобразований столбцов.

Доказательство. Пусть матрица получена из матрицы элементарными преобразованиями столбцов. Тогда матрица получается из матрицы элементарными преобразованиями строк и поэтому . Так как и , то . ■

Таким образом, при вычислении ранга матрицы ее можно приводить к ступенчатому виду, пользуясь одновременно элементарными преобразованиями строк и столбцов.

Замечание. Всякая ступенчатая матрица является верхнетреугольной. Поэтому наиболее эффективным способом вычисления определителей является приведение определителя к ступенчатой форме с помощью элементарных преобразований строк и столбцов.