2. Ступенчатые матрицы.

Определение 6.1. Первый, начиная слева, ненулевой элемент строки будем называть лидером строки или ведущим коэффициентом строки.

Пример. Лидером строки является число 2, расположенное в третьем столбце. Строка (0, 0, 0, 0) не имеет лидера.

Определение 6.2. Матрица называется ступенчатой, если она обладает следующими двумя свойствами:

1) для любых двух ненулевых строк матрицы лидер строки с большим номером всегда расположен правее лидера строки с меньшим номером;

2) нулевые строки (если они есть) расположены в матрице ниже всех остальных.

Это определение можно переформулировать следующим образом. Матрица называется ступенчатой, если она удовлетворяет двум следующим условиям:

1) если лидеры ‑ой и ‑ой строк матрицы расположены в столбцах с номерами и , то ;

2) если ‑ая строка матрицы является нулевой, то ‑ая ее строка, если она существует, также должна быть нулевой.

Примеры ступенчатых матриц:

2	1	9	0	8	0		2	1	9	0	8	0	2
0	4	3	6	2	7		0	0	0	6	2	7	0
0	0	0	5	3	8	;	0	0	0	0	6	8	0	;
0	0	0	0	0	4		0	0	0	0	0	0	0

; ; .

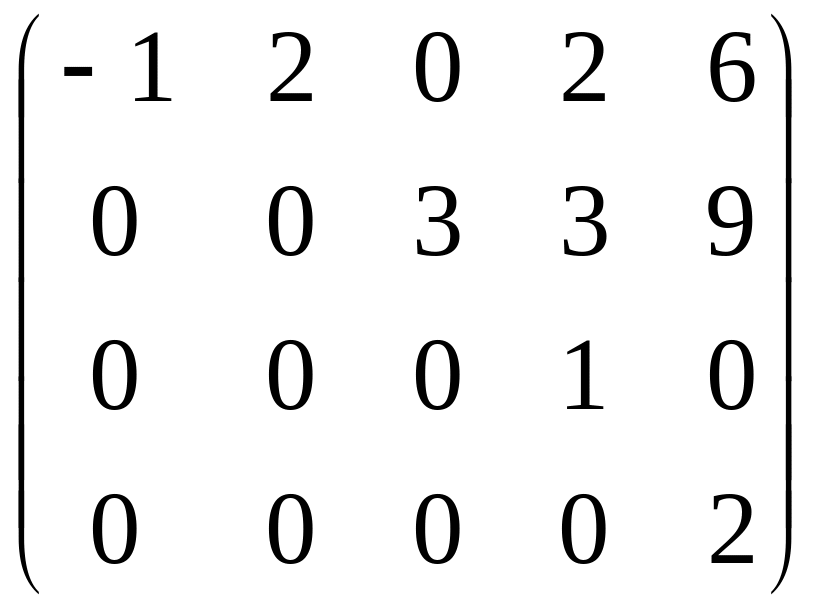Примеры матриц, не являющихся ступенчатыми:

; ; .

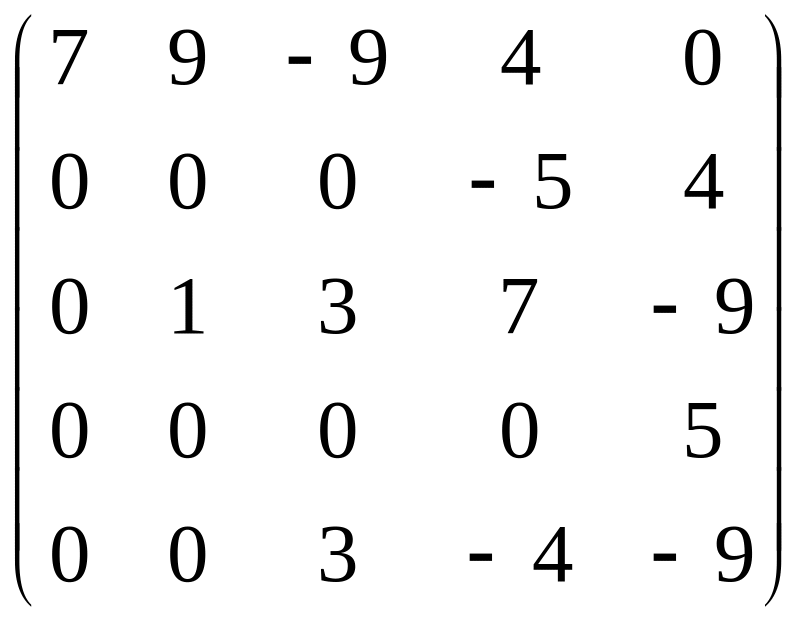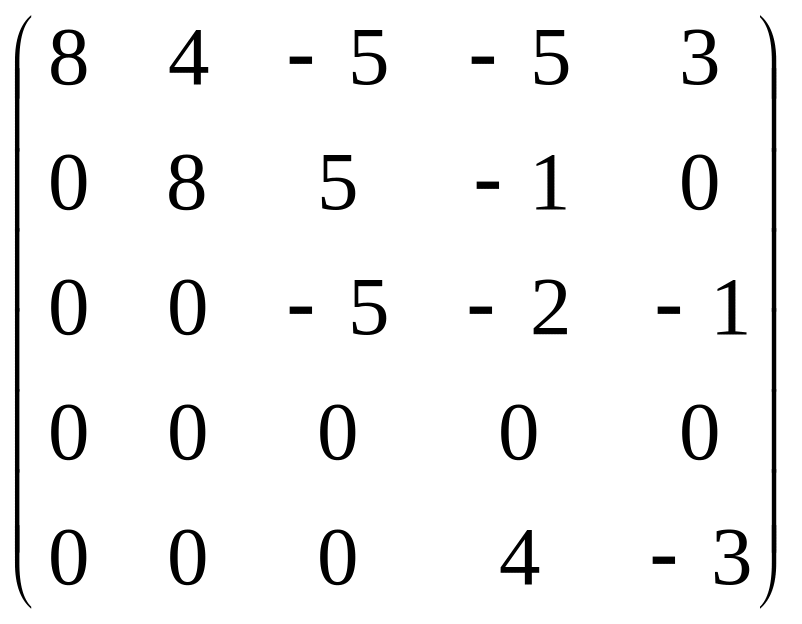Столбцы, в которых расположены лидеры строк ступенчатой матрицы, будем называть базисными.

«Геометрическая интерпретация» свойств ступенчатой матрицы такова. Возьмем в матрице лидер любой ее ненулевой строки. Выделим часть этой строки, расположенную слева от лидера, и выделим часть столбца, в котором находится лидер, расположенную ниже лидера. Вместе с краями матрицы выделенные части строки и столбца образуют прямоугольник. Если матрица является ступенчатой, то все элементы внутри и на границе этого прямоугольника, кроме лидера взятой строки, будут равны нулю. Иначе это свойство можно описать так: все элементы, находящиеся влево и вниз от лидера любой ненулевой строки матрицы, равны нулю. Верно и обратное, если таким свойством обладают лидеры всех ненулевых строк матрицы, то матрица является ступенчатой.

Пример. Выделим все элементы, находящиеся влево и вниз от лидера второй строки ступенчатой матрицы

Дадим еще одно, эквивалентное предыдущим, определение ступенчатой матрицы.

Матрица называется ступенчатой, если для любой ее строки с номером  выполнено следующее, если ‑ая строка ненулевая, то все строки матрицы с большими номерами, если они существуют, начинаются с большего числа нулей, чем ‑ая строка.

О матрице , являющейся ступенчатой, говорят также, что она имеет ступенчатый вид или ступенчатую форму. Ступенчатая матрица , получающаяся из матрицы с помощью конечного числа элементарных преобразований строк, называется ступенчатой формой матрицы .

В главе 1 (см. определение 4.2.) читатель уже познакомился с элементарными преобразованиями строк матрицы. Во многих задачах целью элементарных преобразований строк матрицы является приведение ее к ступенчатому виду. Приведенная ниже теорема играет важную роль в дальнейших теоретических построениях, на ее основе доказываются многие утверждения данной главы.

Теорема 6.3. Всякую матрицу конечным числом элементарных преобразований строк можно привести к ступенчатому виду.

Доказательство. Пусть – матрица размера . Доказательство теоремы будем вести методом математической индукции по числу строк матрицы .

Основание индукции. Пусть , т. е. матрица имеет одну строку . Тогда матрица ступенчатая, поскольку свойства 1) и 2) ступенчатой матрицы в этом случае выполняются в силу того, что в матрице только одна строка.

Шаг индукции. Предположим теперь, что всякую матрицу, имеющую строк, элементарными преобразованиями строк можно привести к ступенчатому виду (в этом состоит предположение индукции), и докажем, что из этого следует, что и всякая матрица , содержащая строк, также приводится элементарными преобразованиями строк к ступенчатому виду.

Если все элементы матрицы равны нулю, то эта матрица ступенчатая и ничего больше доказывать не требуется.

Рассмотрим теперь случай, когда не все элементы матрицы равны нулю. В матрице выберем любую строку, лидер которой расположен в столбце с наименьшим номером . Если выбранная строка не является первой, то переместим ее на место первой строки при помощи элементарного преобразования I-го типа. В результате получим матрицу

в которой , – некоторая матрица размера и – строка длины . Применим теперь преобразования типа II. Из второй строки вычтем первую строку, умноженную на число , и получим во второй строке нуль: . Из третьей строки вычтем первую строку, умноженную на число , и получим во второй строке нуль: , и т. д. Продолжая этот процесс, из -ой строки вычтем первую строку, умноженную на число , получим в последней строке нуль: . Таким образом, совершив преобразований II типа, приходим к матрице

где – матрица размера .

Так как матрица имеет строк, то по предположению индукции матрицу можно привести к ступенчатому виду S с помощью ряда элементарных преобразований. Выполняя эти преобразования над матрицей , мы можем считать, что производим элементарные преобразования над всей матрицей , не использующие ее первой строки. В ходе таких преобразований нули, находящиеся в первом столбце, не могут исчезнуть. Применив аналогичные элементарные преобразования строк к матрице , в результате получим матрицу

Докажем, что матрица является ступенчатой. Лидер первой строки матрицы находится в -ом столбце, а лидеры строк с номерами расположены в подматрице и, следовательно, в столбцах с номерами . Значит условие 1) выполняется, если одна из строк первая. Кроме того, условие 1) выполняется для строк с номерами , так как матрица ступенчатая.

Условие 2) также выполняется, так как нулевые строки матрицы соответствуют нулевым строкам ступенчатой матрицы и поэтому будут расположены ниже всех ненулевых строк. ■

Для элементарных преобразований строк примем следующие условные обозначения:

" " – прибавление к ‑ой строке ‑ой строки, умноженной на некоторое положительное число ;

" " – вычитание из ‑ой строки ‑ой строки, умноженной на некоторое положительное число ;

" " – перестановка ‑ой и ‑ой строк местами;

" " – умножение ‑ой строки на ненулевое число .

Алгоритм приведения матрицы к ступенчатой форме состоит в следующем.

1. В матрице выбирается любая строка, лидер которой расположен в столбце с наименьшим номером. Эта строка перемещается на место первой строки и объявляется разрешающей строкой. Затем проводятся преобразования II типа, обращающие в нуль все элементы, расположенные под лидером первой строки. Для этого разрешающая строка прибавляется с подходящими коэффициентами к остальным строкам матрицы. Если лидер разрешающей строки – число , а в данной строке под ним находится число , то подходящим коэффициентом будет число .

2. Далее преобразования проводятся с подматрицей , состоящей из строк с номерами от 2 до . В матрице выбирается любая строка, лидер которой расположен в столбце с наименьшим номером. Эта строка перемещается на место второй строки матрицы и объявляется разрешающей строкой. Затем проводятся преобразования II типа, обращающие в нуль все элементы, расположенные под лидером разрешающей строки. Для этого разрешающая строка прибавляется с подходящими коэффициентами к остальным строкам матрицы с номерами от 3 до . Первая строка матрицы при этом никак не затрагивается, и поэтому не изменяется.

3. Затем аналогичные преобразования проводятся с подматрицей , состоящей из строк с номерами от 3 до , и т.д.

Пример 6.4. Элементарными преобразованиями строк привести матрицу 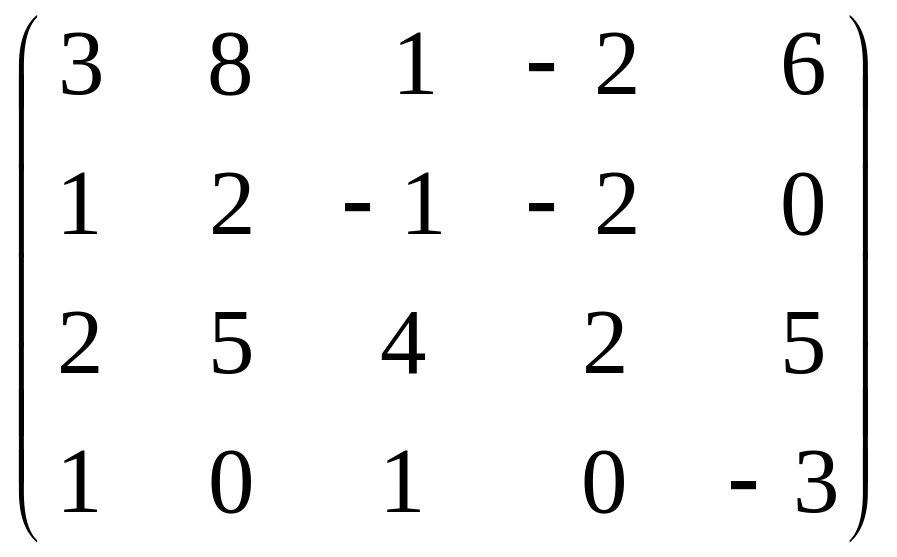к ступенчатой форме.

Решение. Выберем вторую строку в качестве разрешающей и переставим первую и вторую строки местами, поскольку нам удобнее выполнять вычисления с целыми числами, чем с дробями:

Вычтем из второй строки утроенную первую строку, из третьей строки удвоенную первую строку и, наконец, из четвертой строки вычтем первую строку. Все эти преобразования можно записать и выполнить одновременно:

Выберем вторую строку в качестве разрешающей и вычтем из третьей строки вторую строку, умноженную на , а к четвертой строке прибавим вторую строку:

Хотя алгоритм этого не требует, умножим третью строку на , а четвертую на .

Затем вычтем из четвертой строки третью:

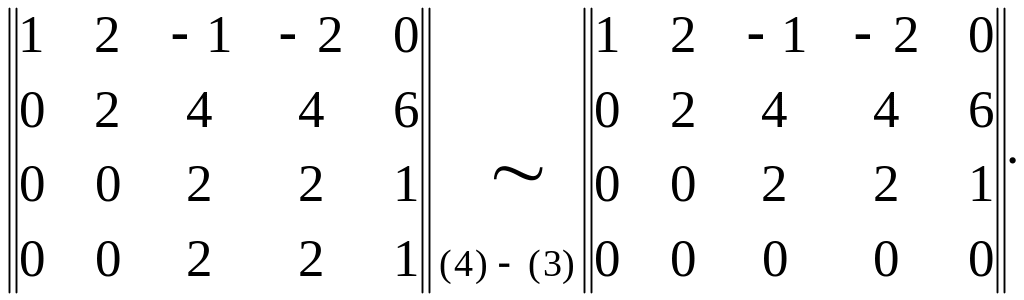
Последняя матрица является ступенчатой.

Определение 6.5. Ступенчатая матрица называется приведенной, если она удовлетворяет двум следующим условиям:

1) лидеры всех строк равны 1;

2) над лидерами строк расположены только нули.

Отметим, что если в приведенной ступенчатой матрице вычеркнуть все небазисные столбцы, то получится единичная матрица.

Теорема 6.6. Всякую матрицу конечным числом элементарных преобразований строк можно привести к приведенному ступенчатому виду.

Доказательство. Согласно теореме 6.3, матрицу можно привести к ступенчатой форме . Поэтому остается доказать, что всякую ступенчатую матрицу конечным числом элементарных преобразований строк можно привести к приведенному ступенчатому виду. Умножим каждую строку ступенчатой матрицы на число , обратное ее лидеру . Тогда лидеры всех строк станут равны 1. Пусть последняя ненулевая строка имеет номер и ее лидер расположен в столбце с номером . Столбец матрицы, содержащий лидер ‑ой строки, имеет вид: . Вычтем из первой строки матрицы ее ‑ую строку, умноженную на число , из второй – ‑ую строку, умноженную на число , и т.д.

Строки с номерами, большими , изменять не будем. В результате столбец примет вид . При этом столбцы с номерами, меньшими , не изменятся, поскольку из их элементов будут вычитаться нули, расположенные левее лидера ‑ой строки. Поэтому матрица не теряет ступенчатого вида.

Рассмотрим теперь -ый столбец, содержащий лидер строки: Вычтем из первой строки матрицы ее ‑ю строку, умноженную на число , из второй – ‑ую строку, умноженную на число , и т.д.

Строки с номерами, большими , изменять не будем. В результате столбец примет вид . При этом матрица не теряет ступенчатого вида, поскольку столбцы с номерами, меньшими , не изменятся.

Продолжая аналогичные преобразования, получим приведенную ступенчатую матрицу. ■

Пример 6.7. Преобразовать ступенчатую матрицу к приведенному ступенчатому виду.

Решение.

.
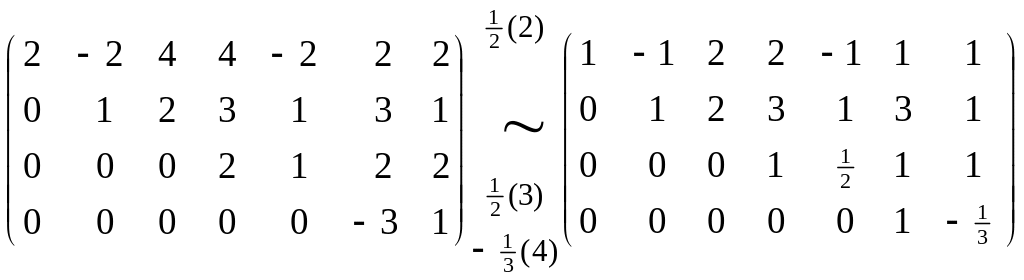