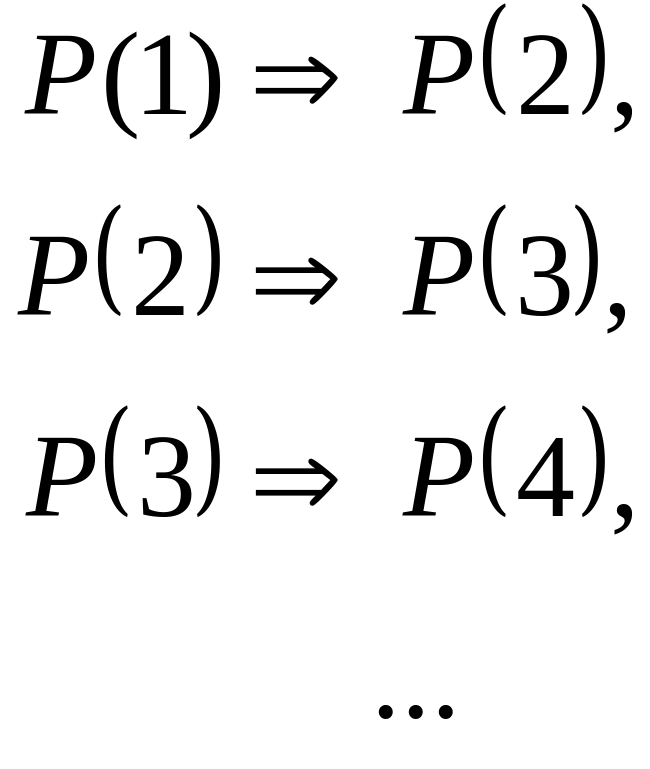§5. Методы вычисления определителей высших порядков

1. Разложение по строке или столбцу. Теорема 3.12 о разложении определителя по строке (столбцу) может быть использована для вычисления определителей.

Пример 5.1. Вычислить определитель , раскладывая по элементам какой-нибудь строки (столбца).

Разложим по элементам второй строки:

;

.

Находим значение каждого из определителей третьего порядка по правилу Саррюса. Получим: .

Необходимо отметить, что такое вычисление не всегда оказывается удобным.

2. Метод понижения порядка состоит в использовании разложения определителя по какой-либо его строке или какому-либо столбцу. Разложение разумно осуществлять по тому ряду определителя, который содержит наибольшее число нулей. Более того, прежде чем применять метод понижения порядка, полезно, используя основные свойства определителей (см. теорему 4.3), обратить в нуль все, кроме одного, элементы его некоторой строки (столбца).

Задача 1. Вычислите определитель

.

Решение. К первой строке прибавим третью строку, умноженную на (–2), а ко второй строке прибавим удвоенную третью строку. Полученный определитель разложим по первому столбцу. Имеем:

Далее можно вынести за знак определителя общий множитель второй строки (число 5) и ко второй строке прибавить третью, умноженную на (–2), а затем вычислить определитель второго порядка:

.

Замечание. Следует обратить внимание на то, что для обращения в нуль некоторых элементов строки (или столбца) используются элементарные преобразования строк и столбцов. Так, в задаче 1 на последнем этапе ко второй строке прибавляли третью, умноженную на (–2). Это же замечание используется и в дальнейшем (задача 2).

3. Метод приведения к верхнетреугольному виду заключается в приведении определителя с помощью элементарных преобразований строк к такому виду, когда все элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. В этом случае величина определителя равна произведению элементов главной диагонали.

Задача 2. Вычислите определитель .

Решение. Прибавим ко второй, третьей и четвертой строке первую строку, умноженную на (–1):

.

Глава 2. Элементарные преобразования матриц

§ 6. Приведение матриц к ступенчатому виду элементарными преобразованиями

1. Принцип математической индукции. Принцип математической индукции является одной из аксиом математической логики. Этот принцип является специальным методом доказательства того, что некоторое утверждение выполнено для всех натуральных чисел.

Принцип математической индукции состоит в следующем.

Пусть – некоторое утверждение, зависящее от натурального числа  . Предположим, что выполнены два условия:

1) истинно;

2) для каждого натурального числа из того, что выполнено, следует, что выполнено.

Тогда утверждение выполнено для всех натуральных чисел .

Отметим, что для доказательства пункта 2) не нужно доказывать, что истинно. Требуется лишь доказать, что если истинно, то также истинно. Предположение, что истинно, называется предположением индукции, а высказывание истинно – основанием индукции. Условие 2):

« выполнено выполнено»

называется шагом индукции.

Если доказан шаг индукции и доказано ее основание , то применение бесконечного числа шагов индукции приводит к следующей бесконечной цепочке истинных утверждений: