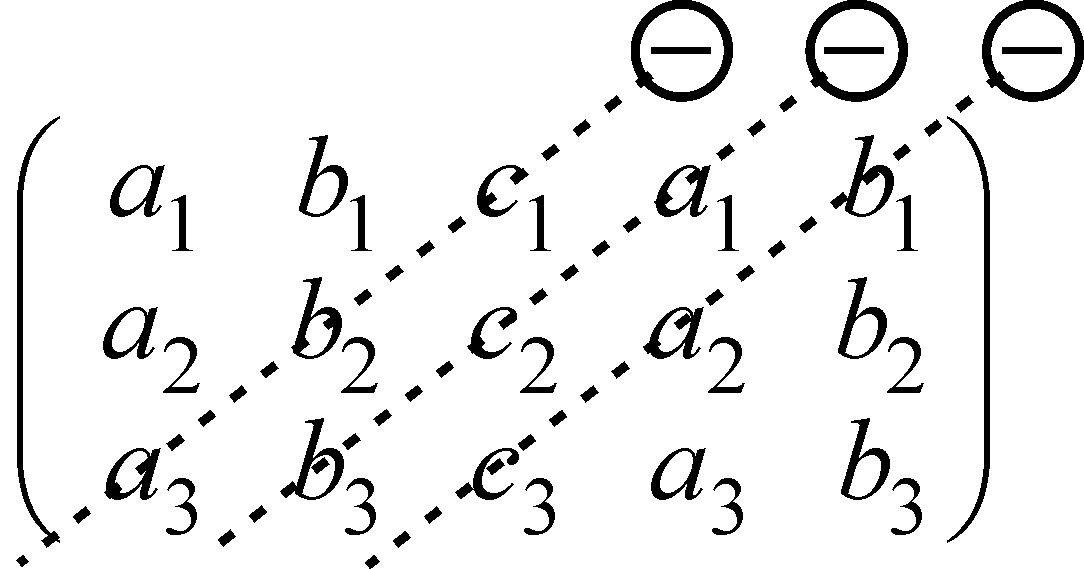§ 3. Понятие определителя квадратной матрицы

1. Определители второго порядка. Рассмотрим квадратную матрицу порядка 2:

.

Диагональ, на которой расположены элементы и , называют главной, а диагональ с элементами и – побочной. Составим два произведения «крест-накрест» и (см. рис. 1), которые мы будем называть членами определителя второго порядка.

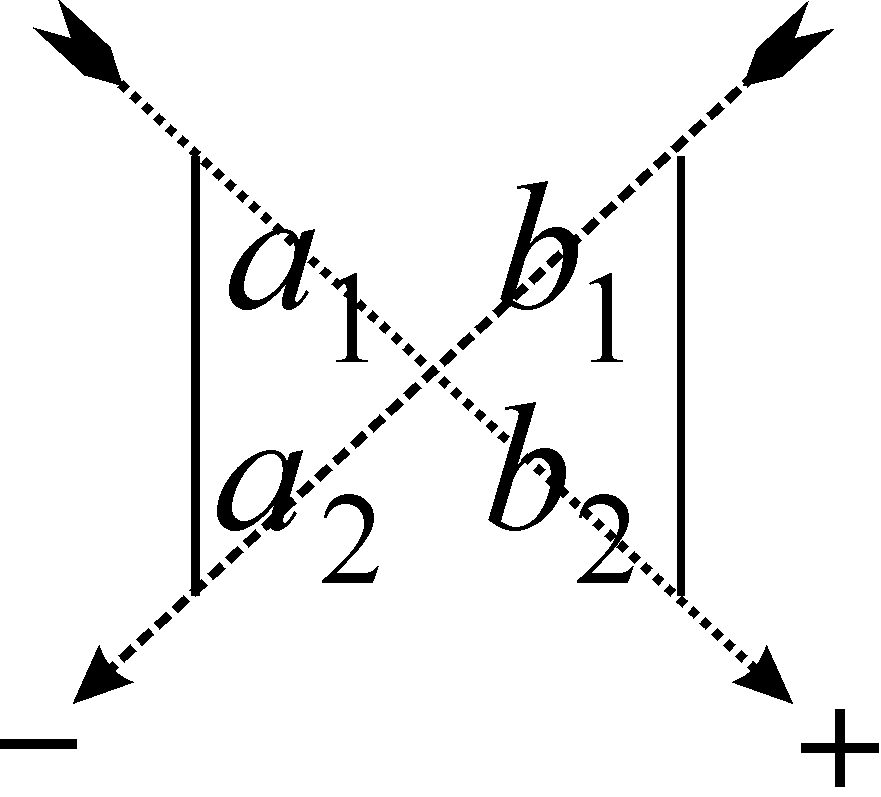
Рис. 1

Если из первого произведения вычесть второе, то полу­чится:

. (1)

Это выражение называется определителем (или детерминантом) второго порядка, составленным из элементов матрицы . Числа называют элементами определителя. Опре­делитель обозначают символом

или .

В последнем обозначении используется сокращение слова «determinant».

Пропорции. Будем говорить, что числа соответственно пропорциональны числам , если либо для некоторого числа , либо для некоторого числа . Пропорцию обычно записывают в виде: . Однако пропорции отличаются от дробей тем, что пропорция вида является верной, а пропорция вида при неверной. Отношение же в пропорциях считается неопределенностью и равно любому отношению, так, например, пропорциональность верна. Легко заметить, что числа пропорциональны числам тогда и только тогда, когда .

Кроме того, наборы чисел и пропорциональны друг другу тогда и только тогда, когда , и .

2. Свойства определителя второго порядка. Докажем несколько свойств определителей порядка 2. Свойства эти интересны по следующим соображениям. С одной стороны, они оказываются верны и для определителей порядка 3, и, вообще, для определителей любого порядка. С другой стороны, доказательства свойств для определителей порядка 2 существенно проще их доказательств в общем случае.

Пусть . Напомним, что матрица называется матрицей, транспонированной к матрице .

Теорема 3.1. Определитель матрицы равен определителю транспонированной матрицы: .

Доказательство.

. ■

Свойство 1. Определитель, две строки (два столбца) которого одинаковы, равен нулю.

Доказательство.

и  ■

Свойство 2. Пусть каждый элемент одного из столбцов (одной из строк) определителя есть сумма двух слагаемых. Например, ; . Тогда опре­делитель равен сумме двух определителей, при­чем в одном определителе этот столбец (строка) состоит из первых слагаемых, а в другом — из вторых слагаемых: .

Доказательство.

 ( ) + ( )  . ■

Свойство 3. Если все элементы какого-нибудь столбца (строки) определителя умножить на одно и то же число k, то значение определителя умножится на k.

Доказательство.

 ■

Свойство 4. Определитель не изменит своего значения, если к одной его строке прибавить другую его строку, умноженную на число. Аналогичное утверждение верно и для столбцов.

Доказательство. Прибавим, например, к элементам второй строки определителя элементы первой строки, умноженной на число  , и вычислим получившийся определитель:

Свойство 5. Если две строки (два столбца) определителя поменять местами, то определитель изменит знак на противоположный, а по абсолютной величине не изменится.

Доказательство

 ■

Свойство 6. Определитель, элементы двух строк (столбцов) которого соответственно пропорциональны, равен нулю.

Доказательство. .■

Пример 3.2. Определитель единичной матрицы равен единице:

3. Определители третьего порядка. Рассмот­рим квадратную матрицу порядка 3:

. (2)

Определение 3.3. Число , сопоставляемое матрице , называется определителем матрицы и обозначается

(3)

Определитель квадратной матрицы порядка 3 называют также определителем третьего порядка. Формулу

(4)

называют разложением определителя по первой строке.

Пример 3.4. Вычислить определитель .

Разложим определитель по элементам первой строки:

Следовательно,

.

Ответ: .

Элементы формируют главную диагональ матрицы (2), а элементы — ее побочную диагональ. Раскрыв скобки в выражении (4), получаем:

(5)

Так как запомнить столь громоздкую формулу трудно, для записи выражения определителя третьего порядка непосредственно через его элементы применяют одно из двух правил: правило треугольников или правило Саррюса.

Правило треугольников. Изображаем главную диагональ матрицы и два треугольника, одно из ребер которых соединяет два элемента матрицы параллельно главной диагонали, а третья вершина — элемент в противоположном углу матрицы (см. рис. 2). Слагаемые, входящие в определитель без дополнительного минуса, — произведения элементов главной диагонали и трех элементов, расположенных в вершинах треугольников.

Рис. 2

Рис. 3

Слагаемые, входящие в (5) с дополнительным знаком «минус», определяются аналогичным образом, но относительно побочной диагонали (рис. 3)

Правило Саррюса. Составим матрицу Саррюса, для этого припишем к матрице (2) ее первый и вто­рой столбцы справа

.

Зачеркиваем всевозможные тройки элементов матрицы Саррюса линиями, параллельными главной диагонали исходной матрицы. Зачеркнув три элемента, записываем их произведение со знаком плюс (см. рис. 4).

Рис. 4

Рис. 5

Аналогичные три произведения, соответствующие прямым, параллельным побочной диагонали, добавляют в формулу с дополнительным знаком «минус» (рис. 5).

Каждое произведение с указанным знаком называется членом определителя (5). Среди входящих в произведения элементов имеются «представители» от каждой строки и от каждого столб­ца.

Пример 3.5. Вычислите определитель .

Решение. Составим матрицу Саррюса: .

Находим члены определителя по правилу Саррюса (рис. 6). Зачеркивая три числа, сразу выписываем их произведение.

Рис. 6

Определитель равен .

Разложение определителя по первому столбцу. Еще один способ вычисления определителя порядка 3 предоставляет формула разложения по элементам первого столбца:

(6)

В частности,

(7)

4. Свойства определителей третьего порядка. Все утверждения, верные для определителей второго (см. пункт 2) порядка, остаются верными и для определителей третьего порядка. Например, так же как и для определителя второго порядка имеет место теорема: определитель матрицы равен определителю транспонированной матрицы: .

Доказательства свойств для определителей третьего порядка ничем не от­личаются от доказательств аналогичных свойств для определи­телей второго порядка и основаны на вычислении определителя третьего порядка по формулам (5) или (4). Рекомендуется эти свойства доказать самостоятельно.

Приведем некоторые из них:

Свойство 1. Определитель, две строки (два столбца) которого одинаковы, равен нулю.

Свойство 2. Пусть каждый элемент одного из столбцов (одной из строк) определителя есть сумма двух слагаемых. Тогда опре­делитель равен сумме двух определителей, при­чем в одном определителе этот столбец (строка) состоит из первых слагаемых, а в другом — из вторых слагаемых.

Свойство 3. Число можно вынести за знак определителя, разделив при этом все элементы одной из его строк на число .

Пример.

Свойство 4. Если из одной строки определителя вычесть (или к одной строке прибавить) другую его строку, умноженную на число, то определитель при этом не изменится. Аналогичное свойство справедливо и для столбцов.

Пример.

Свойство 5. При перестановке двух строк (столбцов) определителя местами определитель меняет свой знак.

Пример.

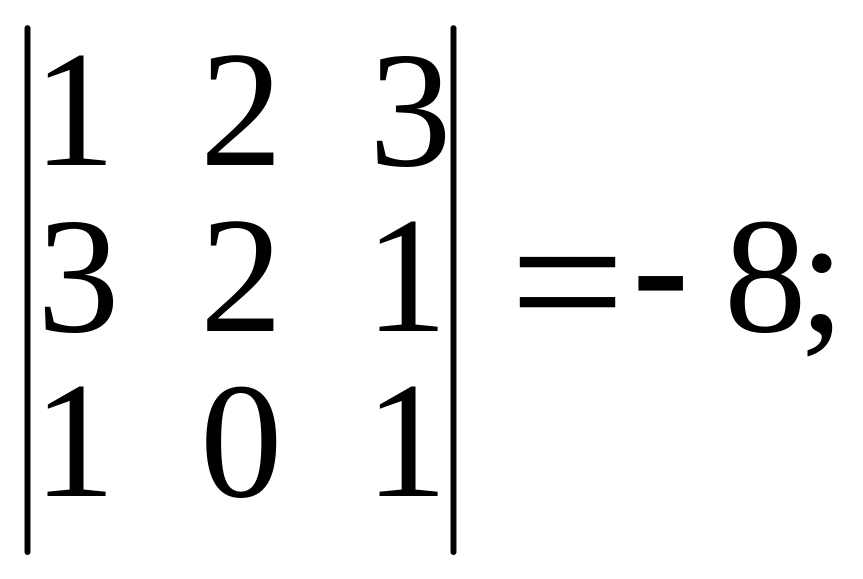
Свойство 6. Определитель, элементы двух строк (столбцов) которого соответственно пропорциональны, равен нулю.

Пример.

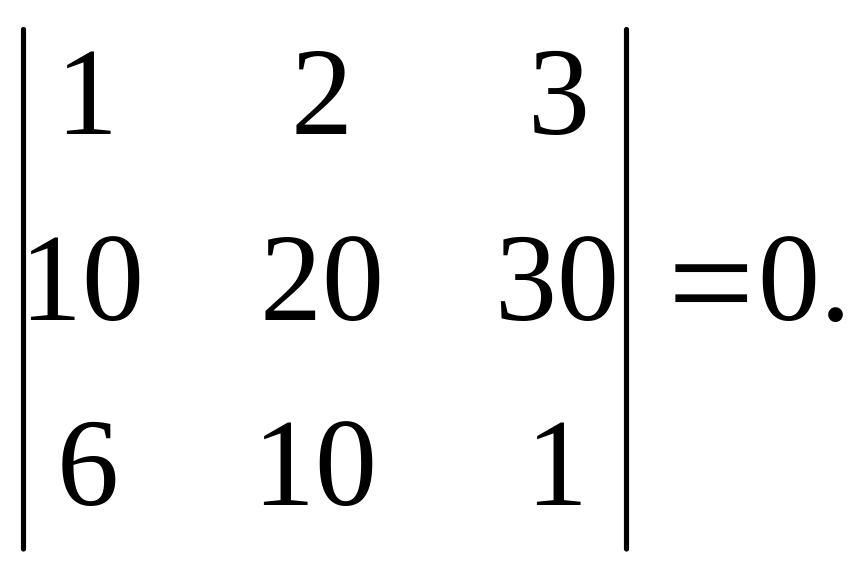
Добавим к этим свойствам еще одно.

Свойство 7. Квадратная матрица вида называется верхнетреугольной. Определитель такой матрицы равен произведению элементов ее главной диагонали

. (8)

Пример 3.6. Вычислить определитель

.

Переставим местами третью и первую строки и получим по свойству 5, что

Используя свойство 3, вынесем множитель за знак определителя из первой его строки:

Вычтем из второй строки определителя его первую строку, умноженную на число . Тогда по свойству 5 имеем:

Отсюда по формуле (7) получаем

.

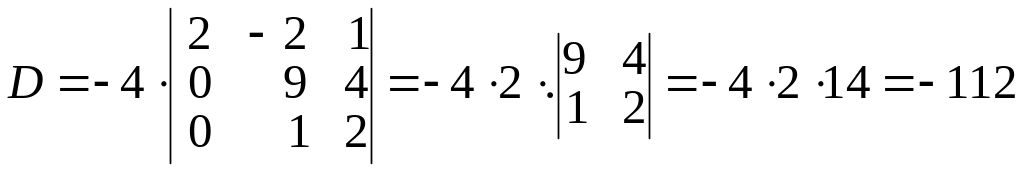5. Миноры и алгебраические дополнения. Для изучения определителей порядка нам потребуются понятия минора и алгебраического дополнения элемента матрицы или определителя.

Определение 3.7. Пусть А – квадратная матрица порядка n. Минором элемента называется определитель порядка , полученный из матрицы А вычеркиванием -ой строки и -го столбца.

Пример 3.8. Найдем минор элемента в матрице

.

Вычеркиваем вторую строку и второй столбец:

.

Из оставшихся после вычеркивания элементов формируем определитель

.

Определение 3.8. Число называется алгебраическим дополнением элемента матрицы А (или в матрице А).

Напомним, что

Выражение для соседних элементов строки (или столбца) всегда приобретает противоположные знаки, так как при изменении или на одну единицу четность числа меняется. Поэтому распределение знаков выражений можно изображать в виде таблицы:

,

которую мы назовем таблицей знаков алгебраических дополнений. Аналогичную таблицу можно составить для матрицы произвольных размеров, соблюдая два правила:

1) в левом верхнем углу должен стоять знак «+»,

2) знаки следуют в таблице в шахматном порядке.

Пример 3.9. Найдем в квадратной матрице порядка 4 из примера 3.8 алгебраическое дополнение элемента  :

Как мы определили знак алгебраического дополнения?

Первый способ. Число 5 нечетно .

Второй способ. Знак алгебраического дополнения находим в таблице:

.

Пример 3.10. .

Задача 1. Найдите миноры и алгебраические дополнения элементов и определителя третьего порядка

.

Решение. Минор получается из данного определителя вычеркиванием первой строки и второго столбца, на пересечении которых стоит элемент :

, .

Минор получаем из определителя вычеркиванием третьей строки и первого столбца, на пересечении которых стоит элемент :

, .

6. Определители высших порядков. В задачах высшей алгебры наряду с определителями второго и третьего порядков встречаются также определители более высоких порядков. Определитель n – го порядка состоит из элементов и имеет n строк и n столбцов. Например, определитель четвертого порядка выглядит так:

,

а определитель произвольного порядка n имеет вид

. (9)

Детерминант квад­ратной матрицы порядка можно определить через детерминанты порядка .

Определение 3.11. Определитель порядка – это чис­ло, сопоставляемое квадратной матрице порядка по описанно­му ниже правилу.

Предположим, что понятие определителя порядка уже введено и имеется способ вычисления определителей поряд­ка  . Рассмотрим произвольную квадратную матрицу

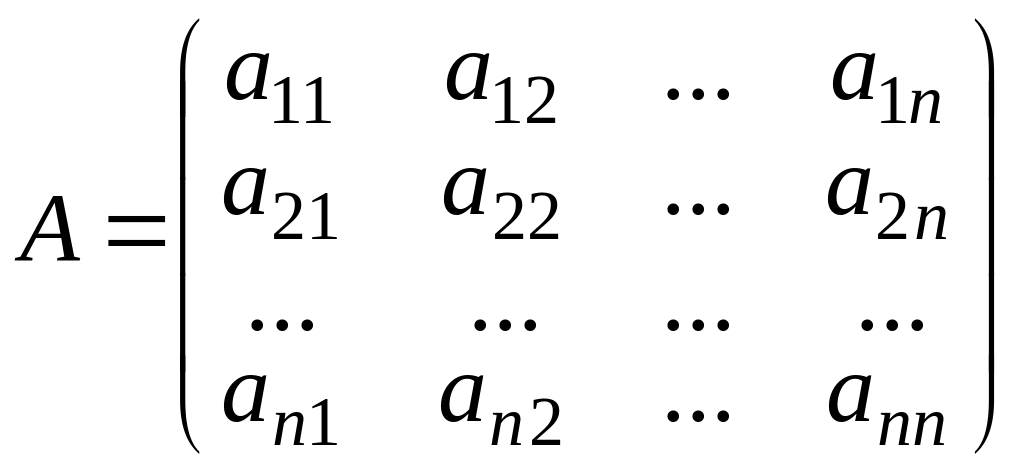
порядка . Тогда определителем матрицы называется число

. (10)

Равенство (10) называется разложением определителя по первой строке.

В §2.2 мы познакомились с методами вычисления определителей порядка 3. Значит, формула (10) позволяет вычислить определитель порядка 4. Но тогда, используя ту же формулу (10), мы можем найти определитель порядка 5 и т. д. Продолжая подобные рассуждения, мы можем «добраться» до любого наперед заданного натурального числа и вычислить определитель порядка .

Таким образом, значение определителя матрицы порядка определяется через значения определителей порядка . Основную техническую трудность при таком способе построения теории определителей представляет доказательство следующей теоремы.

Теорема 3.12. Для каждой строки (и каждого столбца) определителя порядка справедливо следующее утверждение: определитель равен сумме произведений элементов этой строки (этого столбца) на их алгебраические дополнения:

, где , (11)

, где . (12)

Равенство (11) называют разложением определителя по -ой строке, а равенство (12) – разложением определителя по -му столбцу.

Доказательство этой теоремы приведено в §4, а сейчас мы рассмотрим следствия из этой теоремы и примеры решения задач.

Пример 3.13. Выпишем разложение определителя третьего порядка по второму столбцу:

В частности,

Теорема 3.14. Если все элементы -ой строки (или -го столбца), кроме , равны нулю, то .

Доказательство. Для доказательства достаточно заметить, что в формулах разложения по -ой строке ( -му столбцу) все остальные слагаемые, кроме члена , обращаются в ноль. ■

Пример 3.15. Используя теорему 3.12, вычислим определитель . Для этого сначала разложим его по первому столбцу, а затем получившийся определитель порядка 3 разложим по второй строке:

.

Для определителей n-го порядка справедливы свойства определителей, аналогичные свойствам определителей порядка 2 и 3 (см. пункты 2. и 4).