4. Электрическое поле.

Напряженность электрического поля. Физическая величина, равная отношению силы, с которой электрическое поле действует на точечный электрический заряд, к значению этого заряда, называется напряженностью электрического поля. Обозначив напряженность буквой  , запишем

 , (4.1)

где q₁ — заряд, на который действует сила  . Используя закон Кулона и определение понятия напряженности поля, получим выражение для модуля напряженности  электрического поля в некоторой точке А на расстоянии r от точечного заряда q. Если в точку А поместить точечный заряд q₁, то на него будет действовать сила, по закону Кулона равная

.

Для нахождения модуля напряженности электрического поля в точке А разделим модуль силы   на модуль заряда q₁:

 ,

 . (4.2)

Напряженность электрического поля точечного заряда прямо пропорциональна заряду q и обратно пропорциональна квадрату расстояния r от заряда до данной точки поля. Она не зависит от заряда q₁, помещенного в данную точку поля, следовательно, является однозначной силовой характеристикой поля в данной точке. Напряженность электрического поля — векторная величина. За направление вектора   напряженности электрического поля принимается направление вектора кулоновской силы  , действующей на точечный положительный электрический заряд, помещенный в данную точку поля. Зная напряженность электрического поля   в данной точке поля, можно определить модуль и направление силы  ,с которой электрическое поле будет действовать на любой электрический заряд q в этой точке:

. (4.3)

4. Потенциальная энергия заряда в электрическом поле.

Тело массой m в поле тяжести Земли обладает потенциальной энергией.    Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком:

A = -(W_p2 - W_p1) = mgh.

(Здесь и далее мы будем обозначать энергию буквой W.)    Точно так же, как тело массой m в поле силы тяжести обладает потенциальной энергией, пропорциональной массе тела, электрический заряд в электростатическом поле обладает потенциальной энергией W_p, пропорциональной заряду q. Работа сил электростатического поля А равна изменению потенциальной энергии заряда в электрическом поле, взятому с противоположным знаком:

A = -(W_p2 - W_p1) . (5.1)

 Потенциал. В одной точке электростатического поля разные заряды могут обладать различной потенциальной энергией, но отношение потенциальной энергии W_p к заряду q для данной точки поля оказывается постоянной величиной. Эту величину принимают за энергетическую характеристику данной точки поля.     Физическая величина, равная отношению потенциальной энергии электрического заряда в электрическом поле к заряду, называется потенциалом φ  электрического поля:

 .(5.2)

Отсюда потенциальная энергия W_p заряда в электростатическом поле равна произведению заряда q на потенциал φ  электрического поля в данной точке:

 . (5.3)

Значение потенциальной энергии электрического заряда в данной точке электрического поля определяется не только характеристиками электрического поля, но и знаком заряда, помещенного в данную точку поля, и выбором нулевого уровня отсчета потенциальной энергии.     Потенциал — величина скалярная. Если в некоторой точке пространства двумя зарядами одновременно созданы электрические поля с потенциалами   и  , то потенциал   двух электрических полей равен алгебраической сумме потенциалов   и  :

. (5.4)

Аналогичным способом можно найти потенциал электрического поля, созданного любым числом электрических зарядов.

Разность потенциалов. Мерой изменения энергии при взаимодействиях тел является работа. Мы выяснили, что при перемещении электрического заряда q работа А сил электростатического поля равна изменению потенциальной энергии  заряда, взятому с противоположным знаком, поэтому из выражений (5.1) и (5.3) получаем

 . (5.5)

 При перемещении электрического заряда в электростатическом поле работа сил поля равна произведению заряда на разность потенциалов начальной и конечной точек траектории движения заряда.         Если потенциал поля на бесконечно большом расстоянии от точечного электрического заряда в вакууме принимается равным нулю, то на расстоянии r от заряда он определяется по формуле

. (5.6)

 Напряжение. Отношение работы, совершаемой любым электрическим полем при перемещении положительного заряда из одной точки поля в другую, к значению заряда называется напряжением между этими точками:

. (5.7)

Отсюда работа сил электрического поля при перемещении заряда равна произведению напряжения U между точками на заряд q:

A = qU. (5.8)

В электростатическом поле напряжение между двумя любыми точками равно разности потенциалов этих точек:

. (5.9)

Как будет показано далее, равенство (5.9) может не выполняться, если электрическое поле непотенциальное. В непотенциальных электрических полях работа сил поля при перемещении электрического заряда зависит от траектории движения заряда из одной точки в другую.

Единица напряжения и разности потенциалов. Единица напряжения и разности потенциалов в СИ называется вольтом (В):

_{,      .}

Связь напряжения с напряженностью поля. При перемещении положительного заряда q по линии напряженности однородного поля на расстояние d кулоновская сила   совершает работу, равную

.

С другой стороны, работа электрического поля может быть найдена по известному напряжению U между начальной и конечной точками пути:

A = qU

Следовательно, напряжение U между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности   поля на расстояние d между этими точками:

U = Ed. (5.10)

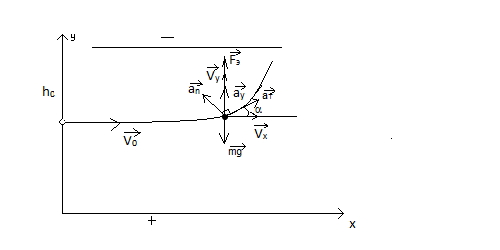
График движения частицы.