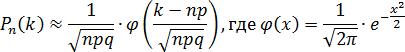
Пример 1.

Вероятность наступления события А в каждом из 900 независимых испытаний равна p = 0,8. Найдите вероятность того, что событие А произойдет 750 раз;

Решение

Так как npq = 900·0,8·0,2 = 16·9 = 144

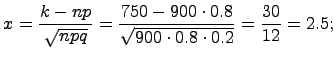
Интегральная теорема Лапласа. Имеет место следующее утверждение.     Теорема: если при большом количестве повторения испытания события А в каждом испытание происходит с постоянной вероятностью Р, то вероятность того, что событие А произойдёт минимум К₁ максимум К₂ раз будет определяться по интегральной теореме Лапласа

Вероятность наступления события А в каждом из 900 независимых испытаний равна p = 0,8. Найдите вероятность того, что событие А произойдет  от 710 до 740 раз.

Наивероятнейшее число появлений события в независимых испытаниях

Число k₀ (наступления события в независимых испытаниях, в каждом из которых вероятность появления события равна р) называют наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях k₀ раз, превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний.

Наивероятнейшее число k₀ определяют из двойного неравенства

np-q≤k₀≤np+p,

причем:

а) если число nр-q — дробное, то существует одно наивероят нейшее чиcло k₀;

б) если число nр-q — целое, то существует два наивероятнейших числа, а именно: k₀ и k₀+1;

в) если число nр—целое, то наивероятнейшее число k₀ = nр.

Вопрос 15

Случайная выборка - способ отбора, при котором каждый элемент генеральной совокупности имеет одинаковую вероятность быть выбранным. Реализовать случайную выборку можно, используя такие приемы, как лотерейный метод и/или таблицу случайных чисел. С помощью этого типа выборки проводится большинство телефонных опросов и опросов по каким-либо спискам (например, избирательным). Для построения случайной выборки необходим список всех элементов генеральной совокупности.

Генеральная совокупность Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и времени. Примеры генеральных совокупностей: - Все жители Москвы (10,6 млн. человек по данным переписи 2002 года) - Мужчины-Москвичи (4,9 млн. человек по данным переписи 2002 года) - Юридические лица России (2,2 млн. на начало 2005 года)

Выборка (Выборочная совокупность) Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна обладать свойством репрезентативности. 

Повторная выборка - отобранный объект возвращается в генеральную совокупность.

Бесповторная выборка – выборка, при которой отобранный объект в генеральную совокупность не возвращается.

Существуют пять основных способов организации выборочного наблюдения:

1. простой случайный отбор, при котором   объектов случайно извлекаются из генеральной совокупности   объектов (например с помощью таблицы или датчика случайных чисел), причем каждая из возможных выборок имеют равную вероятность. Такие выборки называются собственно-случайными;

2. простой отбор с помощью регулярной процедуры осуществляется с помощью механической составляющей (например, даты, дня недели, номера квартиры, буквы алфавита и др.) и полученные таким способом выборки называются механическими;

3. стратифицированный отбор заключается в том, что генеральная совокупность объема   подразделяется на подсовокупности или слои (страты) объема   так что  . Страты представляют собой однородные объекты с точки зрения статистических характеристик (например, население делится на страты по возрастным группам или социальной принадлежности; предприятия — по отраслям). В этом случае выборки называются стратифицированными (иначе, расслоенными, типическими, районированными);

4. методы серийного отбора используются для формирования серийных или гнездовых выборок. Они удобны в том случае, если необходимо обследовать сразу "блок" или серию объектов (например, партию товара, продукцию определенной серии или население при территориально-административном делении страны). Отбор серий можно осуществить собственно-случайным или механическим способом. При этом проводится сплошное обследование определенной партии товара, или целой территориальной единицы (жилого дома или квартала);

5. комбинированный (ступенчатый ) отбор может сочетать в себе сразу несколько способов отбора (например, стратифицированный и случайный или случайный и механический); такая выборка называется комбинированной.

Основные характеристики параметров генеральной и выборочной совокупности

В основе статистических выводов проведенного исследования лежит распределение случайной величины  , наблюдаемые же значения (х₁, х₂, … , х_n) называются реализациями случайной величины Х (n — объем выборки). Распределение случайной величины  в генеральной совокупности носит теоретический, идеальный характер, а ее выборочный аналог является эмпирическим распределением. Некоторые теоретические распределения заданы аналитически, т.е. их параметры определяют значение функции распределения   в каждой точке пространства возможных значений случайной величины  . Для выборки же функцию распределения определить трудно, а иногда невозможно, поэтому параметры оценивают по эмпирическим данным, а затем их подставляют в аналитическое выражение, описывающее теоретическое распределение. При этом предположение (или гипотеза) о виде распределения может быть как статистически верным, так и ошибочным. Но в любом случае восстановленное по выборке эмпирическое распределение лишь грубо характеризует истинное. Важнейшими параметрами распределений являются математическое ожидание   и дисперсия  .

По своей природе распределения бывают непрерывными и дискретными. Наиболее известным непрерывным распределением является нормальное. Выборочными аналогами параметров   и для него являются: среднее значение  и эмпирическая дисперсия  . Среди дискретных в социально-экономических исследованиях наиболее часто применяется альтернативное (дихотомическое) распределение. Параметр математического ожидания   этого распределения выражает относительную величину (или долю) единиц совокупности, которые обладают изучаемым признаком   (она обозначена буквой ); доля совокупности, не обладающая этим признаком, обозначается буквой q (q = 1 — p). Дисперсия же  альтернативного распределения также имеет эмпирический аналог  .

В зависимости от вида распределения и от способа отбора единиц совокупности по-разному вычисляются характеристики параметров распределения. Основные из них для теоретического и эмпирического распределений приведены в табл. 9.1.

Долей выборки k_n называется отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

k_n = n/N.

Выборочная доля w — это отношение единиц, обладающих изучаемым признаком x к объему выборки n:

W_i =n_n/n. ( отношение числа наблюдений к объёму выборки)-относительная частота

n- объём выборки(совокупности)

K-несколько признаков

N-объём генеральной совокупности

х₁ – вариант

х₁, х₂, … , х_{n –} вариационный ряд

F(x) – эмпирическая функция распределения( функция распределения выборки)

n_n – число наблюдений

n_x – число вариант

Вопрос 17

Репрезентати́вность — соответствие характеристик выборки характеристикам популяции или генеральной совокупности в целом. Репрезентативность определяет, насколько возможно обобщать результаты исследования с привлечением определённой выборки на всю генеральную совокупность, из которой она была собрана.

Также репрезентативность можно определить как свойство выборочной совокупности представлять параметры генеральной совокупности, значимые с точки зрения задач исследования.

Пример

Предположим, совокупность — это все учащиеся школы (600 человек из 20 классов, по 30 человек в каждом классе). Предмет изучения — отношение к курению. Выборка, состоящая из 60 учеников старших классов, гораздо хуже представляет совокупность, чем выборка из тех же 60 человек, в которую войдут по 3 ученика из каждого класса. Главной причиной тому — неравное возрастное распределение в классах. Следовательно, в первом случае репрезентативность выборки низкая, а во втором случае репрезентативность высокая (при прочих равных условиях).

Для того чтобы можно было по выборке делать вывод о свойствах генеральной совокупности, выборка должна быть репрезентативной (представительной), т. е. она должна полно и адекватно представлять свойства генеральной совокупности. Репрезентативность выборки может быть обеспечена только при объективности отбора данных.

Способы отбора, обеспечивающие репрезентативность выборки: случайный отбор, отбор единиц по определенной схеме, сочетание первого и второго способов.

Репрезентативность выборки

Свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей.

Пример:

- Выборка, целиком состоящая из москвичей, владеющих автомобилем, не репрезентирует все население Москвы.

- Выборка из российских предприятий численностью до 100 человек не репрезентирует все предприятия России.

- Выборка из москвичей, совершающих покупки на рынке, не репрезентирует покупательское поведение всех москвичей.

В то же время, указанные выборки (при соблюдении прочих условий) могут отлично репрезентировать москвичей-автовладельцев, небольшие и средние российские предприятия и покупателей, совершающих покупки на рынках соответственно.

Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от ошибки никак не зависит от размера выборки.

Пример:

Как бы мы не увеличивали количество опрошенных москвичей-автовладельцев, мы не сможем репрезентировать этой выборкой всех москвичей.

Мат.стат. № 17

формирование и объем репрезентативной выборки

Возникает закономерный вопрос, как сформировать репрезентативную выборку? С точки зрения статистики репрезентативность выборки означает, что представленное в выборке распределение изучаемых признаков соответствует (с определенной долей по грешности) их распределению в генеральной совокупности.

Опишем два метода, обеспечивающие репрезентативность выборки.

Первый метод формирования простой случайной выборки. В этом случае выборка состоит из элементов, отобранных из гене ральной совокупности таким образом, чтобы каждый элемент этой совокупности имел бы равные возможности (равную веро ятность) попасть в выборку. Полученная таким образом выборка называется простой случайной выборкой.

Получить простую случайную выборку можно путем обычной жеребьевки (по аналогии с лотереей) или с помощью специаль ных таблиц случайных чисел. В последнем случае элементы гене ральной совокупности перенумеровываются и из таблицы слу чайных чисел, открытой на произвольной странице, выписыва ются номера элементов, которые должны быть взяты в выборку. Данная процедура трудно осуществима, поскольку для ее реали зации необходимо учитывать каждого представителя генеральной совокупности.

Второй метод основывается на понятии стратифицированной случайной выборки. Для этого необходимо разбить элементы гене ральной совокупности на страты (группы) в соответствии с не которыми характеристиками. Например, при обследовании спро са на некоторый товар генеральную совокупность желательно разбить на группы, различающиеся по величине дохода, соци альной принадлежности или даже по месту жительства (город, деревня). Если произведена подобная разбивка совокупности и случайная выборка производится отдельно из каждой группы (страты), то полученная в итоге выборка носит название стра тифицированная случайная выборка.

Как определяется объем выборки? Подчеркнем, что он зависит прежде всего от задач исследования. Психолог может изучать единичные случаи, если те по каким-либо причинам представляют особый интерес для науки. Так, например, строится работа с одаренными детьми, каждый из которых, как правило, имеет свои неповторимые особенности. Предметом отдельного исследования могут служить также редкие или уникальные случаи на рушения развития. В частности, пристальное внимание известно го ученого П. К. Анохина и его сотрудников было сосредоточено на изучении особенностей функционирования организма сросшихся сиамских близнецов Маши и Даши (это пример так называемой минимальной выборки).

Когда психолог ставит целью изучение характеристик, присущих многим представителям генеральной совокупности, возникает вопрос о наиболее приемлемом объеме выборки. В этих случаях очевидно, что больший объем выборки, позволяет получить более надежные результаты. Объем выборки зависит также от степе ни однородности изучаемого явления. Как правило, чем более однородно изучаемое явление, тем меньше может быть объем выборки. Например, психолог изучает выраженность уровня маску линности—феминности у мастеров спорта по хоккею. Поскольку подобная группа спортсменов представляет собой достаточно однородную выборку, то ее объем может быть весьма небольшим, например, в пределах одной команды — 12—20 человек.

Кроме того, объем выборки зависит от тех статистических методов, которые предполагается использовать. Одни методы требу ют большого количества испытуемых в выборке, другие могут применяться при относительно небольшом их количестве. Напри мер, некоторые непараметрические критерии различий могут использоваться при сравнении групп численностью в 5—7 человек, а факторный анализ наиболее адекватен, если объем выборки со ставит около 100 человек.

Для психологических исследований рекомендуется использовать экспериментальную и контрольную группы, так чтобы численность обоих сравниваемых групп была не менее 30—35 испытуемых в каждой.

1 Вероятностная и невероятностная выборки

Фундаментальное различие между выборками состоит в их принадлежности к вероятностным или невероятностным выборкам. Вероятностную выборку еще часто называют случайной выборкой, и только в отношении случайных, или вероятностных, выборок можно быть уверенными, что они лишены тенденциозности. В соответствии с определением все члены генеральной совокупности случайной выборки имеют равные шансы быть в ней представленными, и самый очевидный пример случайной выборки — это обычная лотерея. Все шары или числа, остающиеся в розыгрыше, сохраняют равные шансы быть выбранными в следующий раз. Ясно, что никакая тенденция не влияет на выбор чисел в лотерее.

ВОПРОС № 19.

То́чечная оце́нка в математической статистике — это число, вычисляемое на основе наблюдений, предположительно близкое к оцениваемому параметру

Мода - это просто наиболее часто встречающееся в определенной совокупности наблюдений значение переменной. При сгруппированных данных мода определяется как середина интервала группирования, содержащего наибольшее число значений наблюдаемой переменной.

Медиана - это значение переменной, делящее упорядоченную совокупность наблюдений пополам, так что одна половина значений в этой совокупности лежит ниже медианы, а др. их половина - выше медианы. Если совокупность образована нечетным числом значений наблюдаемой переменной, то медиана равна значению переменной, являющемуся серединой упорядоченной совокупности наблюдений. Если же совокупность образована четным числом значений, то медиана определяется значением, лежащим посередине между двумя значениями, находящимися в центре упорядоченной совокупности наблюдений. Медиана - более полезная мера, чем мода, и часто используется в случае скошенного (асимметричного) распределения данных. Следует, однако, отметить, что медиана нечувствительна к величине крайних значений упорядоченной совокупности наблюдений.

Среднее арифметическое - самая распространенная мера центральной тенденции - определяется как сумма значений наблюдаемой переменной, разделенная на их число. (В данной статье под «средним» подразумевается среднее арифметическое.) Использование среднего дает исследователю ряд преимуществ. В отличие от др. М. ц. т., среднее чувствительно к точному положению каждого значения в распределении переменной. Правда, это достоинство среднего арифметического оборачивается недостатком в виде повышенной чувствительности к крайним значениям переменной, и потому его иногда избегают использовать в случае сильно скошенных распределений.

Более простые определения.

сре́днее арифмети́ческое ( Формула: M = ) - одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их количество.

Медиана (Обозначаеться Me)  – значение, которое делит упорядоченные по возрастанию (убыванию) наблюдения пополам ( формула: N + 1, а потом делим на 2)

Мода – наиболее часто встречающееся значение (обозначается M нулевое - Мо)

Меры центральной тенденции (более развёрнутый вариант).

Рассматривая методы математической статистики, применяемые для обработки данных тестовых исследований, можно выделить группу методов которые могут описывать те или иные меры центральной тенденции. Такие меры указывают наиболее типичный результат, характеризующий выполнение теста всей группой. Самая известная из таких мер -среднеарифметическое значение (М).

Среднеарифметическое (или выборочное среднее) значение представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута исследованию (выборка испытуемых). Сравнивая среднее значение двух или нескольких групп, мы можем судить об относительной степени развития у людей, составляющих эти группы, оцениваемого качества

Среднеарифметическое определяется по следующей формуле:

М = 

где М - среднеарифметическое значение

n - количество испытуемых

Пример: В исследовании объема вербальной механической памяти, тест ``10 слов'' в группе из 12 испытуемых (n = 12), получены следующие результаты (количество запомненных слов): 5, 4, 5, 6, 7, 3, 6, 2, 8, 6, 9, 7

Среднеарифметическое значение (М) 

Для данной выборки среднеарифметическое значение (М) = 5,6

Другой мерой центральной тенденции является мода (Мо) - наиболее часто встречающийся результат. В интервальном частотном распределении мода определяется как середина интервала, для которого частота максимальна.

Пример: В ряду значений 2, 3, 4, 5, 5, 6, 6, 6, 7, 7, 8, 9 модой является 6, потому, что 6 встречается чаще любого другого числа.

Обратите внимание, что мода представляет собой наиболее часто встречающееся значение (в данном примере это 6), а не частоту встречаемости этого значения (в данном примере равную 3).

Когда два соседних значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений.

Пример: в выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом расположенных значений 2 и 5 совпадают и равняются 3. Эта частота больше, чем частота других значений 1 и 6 (у которых она равна 1). Следовательно, модой этого ряда будет величина 

Третья мера центральной тенденции - медиана (Ме), - результат, находящийся в середине последовательности показателей, если их расположить в порядке возрастания или убывания. Справа и слева от медианы (Ме) в упорядоченном ряду остается по одинаковому количеству данных (50% и 50%). Если ряд включает в себя четное количество признаков, то медианой (Ме) будет среднее, взятое как полусумма двух центральных значений ряда.

Пример: Найдем медиану выборки: 5, 4, 5, 6, 7, 3, 6, 2, 8, 6, 9, 7.

Упорядочим выборку: 2, 3, 4, 5, 5, 6, / 6, 6, 7, 7, 8, 9. Поскольку здесь имеется четное число элементов, то существует две ``середины'' - 6 и 6. В этом случае медиана определяется как среднее арифметическое этих значений.

Ме 

Пример: Найдем медиану выборки с нечетным количеством значений: 9, 3, 5, 8, 4, 11, 13.

Сначала упорядочим выборку по величинам входящих в нее значений. Получим: 3, 4, 5, 8, 9, 11, 13. Поскольку в выборке семь элементов, четвертый по порядку элемент будет серединой ряда. Таким образом, медианой будет четвертый элемент - 8

Значения Ме и Мо полезны для того, чтобы установить является ли распределение частных значений изучаемого признака симметричным и приближающимся к нормальному распределению. Среднее арифметическое (М), медиана (Ме) и мода (Мо) для нормального распределения обычно совпадают или очень мало отличаются друг от друга. При нормальном распределении результатов график распределения имеет форму колокола (рис. 2).

20. Характеристики изменчивости: выборочная дисперсия, выборочное стандартное отклонение.

Выборочная дисперсия.

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию.

  Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения признака выборки различны, то

если же все значения имеют частоты n₁, n₂,…,n_k, то

Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

  Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:

Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:

Замечание: если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.