1. Матрицы: основные определения, операции над матрицами, их свойства

Основные понятия и обозначения. Пусть m и n два произвольных натуральных числа. Матрицей размера m на n (записывается так )называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.

Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицы обозначают строчными латинскими буквами, снабженными двумя индексами: - элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом

Определение 1. Таблица, состоящая из m x n чисел, расположенных в m строках и n столбцах, называется матрицей размера m x n, а числа, из которых она составлена, называются элементами матрицы.

Приняты следующие обозначения матрицы:

(1.2)

Элементы матрицы можно обозначить a_ij, где i - номер строки, а j - номер столбца, в которых расположен элемент.

Если m = n, то матрица называется квадратной, а число n - ее порядком. Элементы матрицы а₁₁, a₂₂, ..., a_nn называют главной диагональю, а элементы a_1n, a_2n-1,..., a_n1 побочной диагональю.

Матрица размера m x n составленная из коэффициентов системы (1.1), называется матрицей системы, а матрица размера m x (n+1),

, (1.3)

полученная из матрицы системы путем приписывания столбца из свободных членов, называется расширенной матрицей системы. Очевидно, что любая система линейных уравнений определяет единственную расширенную матрицу размера m x (n+1) и любая матрица определяет единственную систему линейных уравнений.

Изучение матриц, как математических объектов, представляет самостоятельный интерес, так как матрицы широко используются не только при исследовании и решении систем линейных уравнений. Рассмотрим частные виды матриц.

Виды матриц:

1. Если m = 1, матрица А называется матрицей-строкой.

.

2. Если n = 1, матрица А называется матрицей-столбцом.

.

3. Нулевой называется матрица, состоящая из нулей.

4. Квадратная матрица, у которой все элементы, расположенные ниже (выше) главной диагонали, равны нулю, называется верхней (нижней) треугольной матрицей.

5. Если все элементы, расположенные ниже и выше главной диагонали квадратной матрицы, равны нулю, то такая матрица называется диагональной.

6. Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной и обозначается буквой Е.

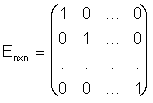. (1.4)

7. Если строки матрицы А (1.2) превратить в столбцы с сохранением номера, то получим новую матрицу n x m, которая называется транспонированной по отношению к матрице А и обозначается А^Т.

(1.5)

8. Матрица вида

(1.6)

называется трапециевидной.

Операции над матрицами

Линейными операциями над какими либо математическими объектами называются операции сложения и умножения на число.

Определение 1. Две матрицы А и В равны (А=В), если их размеры совпадают и элементы, стоящие на одинаковых местах равны между собой.

Определение 2. Суммой двух матриц А=(а_ij)_{m x n} и B=(b_ij)_{m x n} одинаковых размеров называется матрица С=(с_ij)_{m x n} , обозначается С=А+В, тех же размеров, элементы которой c_ij = a_ij + b_ij.

Пример.

  .

Определение 3. Произведением матрицы А=(а_ij)_{m x n} на число l называется матрица того же размера, что и матрица А, элементы которой равны произведениям соответствующих элементов матрицы А на число l .

Пример.

  .

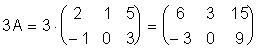Определение 4. Две матрицы A_{m x k} и B_{k x p} называются согласованными, если число столбцов матрицы А совпадает с числом строк матрицы В. Операция умножения матриц рассматривается только для согласованных матриц.

Определение 5. Произведением матрицы A_{m x k} = (a_ij) на матрицу B_{k x p} = (b_ij) называется матрица C_{m x p} = (c_ij), такая, что:

с_y = a_i1b₁j + a_i2b_2j +... + a_ikb_kj.

Произведение обозначается А^.В. Из определения следует, что элемент матрицы А^.В, стоящий в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.

Примечание. Если произведение А^.В существует, то произведение В^.А, вообще говоря, существует. Если А^.В и В^.А существуют, то, возможно А^.В не равно В^.А.

Свойства операций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A')'=A

(λA)'=λ(A)'

(A+B)'=A'+B'

(AB)'=B'A'