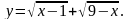Самостоятельная работа по теме «Точки экстремума функции»

Вариант 2.

№1. Перепишите и допишите предложения:

а) Точку х=х₀ называют точкой минимума функции у=f(x), если……….

б) Точки экстремума - это……..

в) Стационарные точки функции – это………….

г) Теорема. Если в точке х₀ производная меняет знак…………., то х₀ – точка максимума.

№ 2.

Критические точки: Стационарные точки:

Точки минимума: Точки экстремума:

Урок №5. Наибольшее и наименьшее значение функции (1 ч.).

Изучение нового материала:

- понятие наибольшее/наименьшее значения функции.

Понятия вводятся конкретно-индуктивным методом. Сначала приводится пример, из которого выводится понятие.

Цель: ввести понятие наибольшего/наименьшего значения функции.

Возможно применение наглядного материала в виде электронной презентации.

Закрепление новых понятий осуществляется на примере четырех задач:

1., 2. Найти наибольшее/наименьшее значения функции на отрезке.

3. Записать число в виде произведения двух положительных чисел, сумма которых наименьшая.

4. Из всех прямоугольников, вписанных в окружность данного радиуса, найти прямоугольник наибольшей площади.

Урок №6. Нахождение наибольшего/наименьшего значений функции. Самостоятельная работа. (1 ч.)

Цель: повторить изученный материал; самостоятельная работа.

Решение задач по изученной теме:

№ 936 (отработка понятий «экстремум функции», «наибольшее/наименьшее значения функции»);

№ 937 - 942 (отработка понятия «наибольшее/наименьшее значения функции»);

Домашнее задание:

№ 943, 946, 947.

Самостоятельная работа.

1 Вариант.

№948, № 950.

2 Вариант.

№ 949, № 951

Урок №7. Производная II порядка, выпуклость, точки перегиба (1 ч.).

Изучение нового материала:

- производная второго порядка;

- выпуклость функции;

- точка перегиба.

Понятия вводятся конкретно-индуктивным методом. Сначала приводится пример, из которого выводится понятие.

Цель: ввести понятие производной второго порядка, выпуклости функции, точки перегиба.

Возможно применение наглядного материала в виде электронной презентации.

Закрепление новых понятий осуществляется на примере задач типа:

1. Найти интервалы выпуклости вверх и вниз функции.

2. Применение свойства выпуклости функции при решении неравенств.

3. Найти точки перегиба функции.

Домашнее задание:

№ 953, № 954, № 955.

Урок №8. Построение графика функции (1 ч.).

Цель: применить производную к построению графика функции.

Возможно применение наглядного материала в виде электронной презентации.

Закрепление новых понятий осуществляется на примере задач типа:

1. Построить график функции.

Урок №9. Решение упражнений по теме «Построение графиков функций» (1 ч.).

Цель: повторить изученный материал.

Решение задач по изученной теме:

№ 923 - 930 (отработка алгоритма построения графика функции и применения производной к построению);

Домашнее задание:

№ 931 -935.

Урок №10. Контрольная работа (1 ч.).

Цель: проверить и оценить знания учащихся.

1 ВАРИАНТ	2 ВАРИАНТ
1. Найдите критические, стационарные точки и точки экстремума функции.
а) б)	а) б)
2. При каких значениях параметра р функция возрастает на всей числовой прямой.	2. При каких значениях параметра р функция убывает на всей числовой прямой.
3. Найдите множество значений функции
4. Длина, ширина и высота прямоугольного параллелепипеда с квадратным основанием составляет в сумме 36 см. Чему равен наибольший объём такого параллелепипеда?	4. Площадь прямоугольного треугольника 8 см2 . Какими должны быть длины сторон треугольника, чтобы сумма площадей квадратов, построенных на его сторонах, была наименьшей?
5. Построить график функции.