17. Вычисление угла между плоскостями у гол между плоскостями.

^{Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.}

^{Двугранный угол между плоскостями равен углу образованному прямыми} 

l₁ и l₂^{, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.}

^{Если заданы уравнения плоскостей A}₁^{x+ B}₁^{y+ C}₁^{z+ D}₁ ^{= 0 и A}₂^{x+ B}₂^{y + C}₂^{z + D}₂ ^{= 0, то угол между плоскостями можно найти, используя следующую формулу}

cosα =	|A1·A2 + B1·B2 + C1·C2|
	( 1 + 1 + 1) (  +  + )

^{Пример. Найти угол между плоскостями 2x+ 4y - 4z - 6 = 0 и 4x+ 3y + 9 = 0.}

^{Решение. Подставим в формулу вычисления угла между плоскостями соответствующие коэффициенты:}

cos α =	|2·4 + 4·3 + (-4)·0|	=	|8 + 12|	=	20	=	2
	(22 + 42 + (-4)2) (42 + 32 + 02)		(36) (25)		30		3

Ответ: косинус угла между плоскостями равен cos α =2/3

19. Прямая в пространстве: общие, параметрические и канонические уравнения, их эквивалентность; уравнения прямой, проходящей через две данные точки.

20. Плоскость и прямая в пространстве. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости. Пересечение прямой и плоскости.

Плоскость и прямая в пространстве.

Уравнение плоскости: Ax + By + Cz +D = 0   

Вектор n , ортогональный плоскости, называется нормальным вектором плоскости.

2. Уравнение плоскости, проходящей через точку  , перпендику­лярно вектору   и имеет вид:

.

Угол между прямой и плоскостью.

 Синус угла   между прямой   и плоскостью   равен косинусу угла   между нормалью ( ) к плоскости и направляющим вектором прямой ( ), поскольку эти два угла в сумме равны 90°.

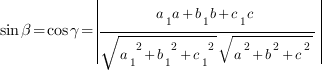
Условия параллельности и перпендикулярности прямой и плоскости.

Условие параллельности прямой и плоскости

Аl + Вm + Сn = 0

Условие перпендикулярности прямой и плоскости

Пересечение прямой и плоскости.

Возможны три варианта взаимного расположения прямой и плоскости в пространстве:

прямая лежит в плоскости;

прямая параллельна плоскости;

прямая пересекает плоскость

Точка пересечения прямой и плоскости

Дана плоскость Ах + Ву + Сz +Д = 0, и прямая 

Тогда точка пересечения (x, y, z): 

21. Кривые 2-го порядка: эллипс, гипербола, парабола.

Общий вид линии второго порядка:

.

К кривым второго порядка относятся: окружность, эллипс, гипербола, парабола.

Эллипс

Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.

Каноническое (простейшее) уравнение эллипса с центром в начале координат и с фокусами в точках и

Где a и b – полуоси эллипса, с – полуфокусное расстояние. Коэффициенты a,b и с эллипса связаны соотношением a2 = b 2 + c 2.

Если центр эллипса находится в точке , то уравнение имеет вид:

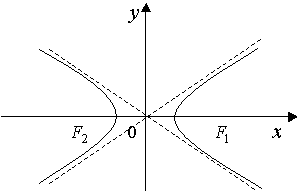
Гипербола

Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Уравнение гиперболы с центром в начале координат и с фокусами в точках

и имеет вид:

Где a– действительная полуось,

b – мнимая полуось.

Коэффициенты a.b и с гиперболы связаны соотношением с2 = a 2 + b 2.

уравнения двух асимптот имеют вид:

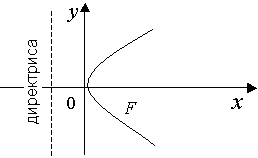
Парабола

Параболой называется множество точек плоскости, равноудаленных от точки, называемой фокусом и прямой, называемой директрисой.

Уравнение параболы с вершиной в начале координат имеет вид: y2 = 2px

где p – расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты