Уравнение прямой по точке и угловому коэффициенту

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить 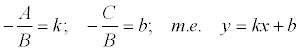 , то полученное уравнение называется уравнением прямой с угловым коэффициентом k .

Уравнение прямой, проходящей через две точки

Пусть в пространстве заданы две точки M ₁ ( x ₁ , y ₁ , z ₁ ) и M₂ ( x ₂, y ₂ , z ₂ ), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:

если х ₁ ≠ х₂ и х = х ₁ , если х ₁ = х₂ .

Дробь 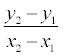 = k называется угловым коэффициентом прямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение. Применяя записанную выше формулу, получаем:

12.Нормаль прямой

Здесь p - длина перпендикуляра, опущенного из начала координат на прямую, измеренная в единицах масштаба, а - угол, который этот перпендикуляр образует с положительным направлением оси Ox. Отсчитывается этот угол от оси Ox против часовой стрелки. Для приведения общего уравнения прямой (2) к нормальному виду обе его части надо умножить на нормирующий множитель: (5) причем перед дробью следует выбрать знак, противоположный знаку свободного члена C в общем уравнении прямой (2). Особенности нормального уравнения прямой: сумма квадратов коэффициентов при текущих координатах равна единице, свободный член отрицателен, а правая его часть равна нулю.

13. Вычисление угла между прямыми.

Вычисление угла между прямыми.

Задача вычисления угла между двумя прямыми в пространстве решается так же, как и на плоскости (§ 32). Обозначим через φ величину угла между прямыми l₁ и  l₂, а через ψ — величину угла между направляющими векторами а и b  этих  прямых.

Тогда, если

ψ <90° (рис. 206, а), то φ = ψ; если же ψ > 90° (рис. 206,6), то φ = 180° — ψ. Очевидно, что в обоих случаях верно равенство cos φ = |cos ψ|. По формуле (1) § 20 имеем

следовательно,

Пусть прямые заданы своими каноническими уравнениями

Тогда угол φ между прямыми определяется с помощью формулы

         (1)

Если одна из прямых  (или обе) задана не каноничecкими уравнениями, то для вычисления угла нужно найти координаты направляющих векторов этих прямых, а затем воспользоваться формулой (1).

14. Условия параллельности и перпендикулярности прямых.

Условия параллельности и перпендикулярности прямых линий

Условие параллельности

       Если прямые линии параллельны, то они наклонены к числовой оси ОХ под одним и тем же углом, следовательно, разница углов наклона параллельных прямых равна нулю (действительно они никогда не пересекаются). Тангенс угла в ноль градусов (ноль радиан) равен нулю. То есть левая часть уравнения равна нулю, тогда нулю должна быть равна и правая часть данного выражения. Дробь равна нулю если числитель равен нулю. В нашем случае это может быть при:

k2 = k1

Это и есть условие параллельности двух прямых линий.

Условие перпендикулярности

Если две прямых линии взаимно перпендикулярны, то угол между ними равен 90 или П/2 радиан. Тангенс такого угла не существует (иногда говорят, что он равен бесконечности). Правая часть не существует при равенстве нулю знаменателя, т.е.

k2 * k1 = -1

Условие k2 * k1 = -1 или что тоже самое   является условием перпендикулярности заданных прямых.

Скалярное произведение векторов

                  Скалярным произведением векторов называется произведение длин (модулей) этих векторов на косинус угла между их направлениями.

                 

Скалярное произведение векторных величин чаще всего принято обозначать точкой (математический знак умножения).

Заметим, что

 и 

Являются соответственно проекциями одного вектора на направление другого вектора, тогда можно записать

.

Таким образом скалярное произведение двух векторов равно длине одного вектора из них, умноженной на проекцию другого вектора на направление первого.

Физический смысл скалярного произведения состоит в том, что вычисляется работа постоянной силы и что соответствует затратам энергии на выполнение данной работы.

Скалярное произведение обладает следующими основными свойствами:

1)  скалярное произведение двух векторов не зависит от порядка сомножителей (переместительное свойство) a*b=b*a;

2)  для трех векторов a, b и c справедливо распределительное свойство (a+b)*c=a*(b+a)*c;

3)  скалярный квадрат вектора равен квадрату модуля этого вектора  ;

4)  скалярный множитель можно выносить за знак скалярного произведения  ;

5)  скалярное произведение линейной комбинации векторов на произвольный вектор равно такой же линейной комбинации данных векторов на этот вектор  .

Исходя из определения скалярного произведения вытекает, что

.                      

то важная формула, позволяющая аналитически определить угол между векторными величинами.

Свойства скалярного произведения

    1. Скалярное произведение обладает переместительным свойством: ab=ba

  

                       

5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0 b, то а  b

.

15. Плоскость в пространстве: общее уравнение; уравнение в отрезках; уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору; уравнение плоскости, проходящей через три данные точки

Общее уравнение плоскости

Пусть в трехмерном пространстве задана прямоугольная декартова система координат.

Общим уравнением плоскости в пространстве называется уравнение вида

Ax + By + Cz + D = 0,

где A2 + B2 + C2 ≠ 0 .

В трехмерном пространстве в декартовой системе координат любая плоскость описывается уравнением 1–ой степени (линейным уравнением). И обратно, любое линейное уравнение определяет плоскость.

Уравнение плоскости в отрезках 

где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Сформулируем следующую задачу:

Составить уравнение плоскости, проходящей через данную точку M(x0,  y0,  z0) перпендикулярно данному вектору 

→

n= {A, B, C} .

Решение. Пусть P(x, y, z) — произвольная точка пространства. Точка P принадлежит плоскости тогда и только тогда, когда вектор MP = {x − x0, y − y0, z − z0} ортогонален вектору 

→

n = {A, B, C}

(рис.1).

Написав условие ортогональности этих векторов (

→

n

, MP) = 0 в координатной форме, получим:

A(x − x0) + B(y − y0) + C(z − z0) = 0

(1)

Это и есть искомое уравнение. Вектор 

→

n= {A, B, C} называется нормальным вектором плоскости.

 Таким образом, чтобы написать уравнение плоскости, нужно знать нормальный вектор плоскости и какую–нибудь точку, принаждежащую плоскости.

Если теперь в уравнении (1) раскрыть скобки и привести подобные члены, получим общее уравнение плоскости:

Ax + By + Cz + D = 0 ,

где D = −Ax0 − By0 − Cz0 .

Уравнение плоскости, проходящей через три точки  М0(x0, y0, z0), М1(x1, y1, z1) и М2(x2, y2, z2), не лежащие на одной прямой, имеет вид

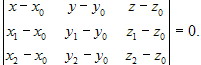
       Параметрическое уравнение.Так же, как для прямой, условие (5.3.1) может быть переписано в виде 

r = r0 + up1 + v2,      u, v ∈ R,        (5.3.3)

или, в координатной форме, в системе координат Oxyz 

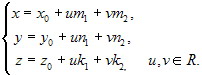                   (5.3.4)

        Уравнения (5.3.3), (5.3.4) называются параметрическими уравнениями плоскости в векторной и координатной формах. 

16. Нормаль плоскости.

Нормаль

Нормаль - это перпендикуляр к касательной прямой или плоскости, проходящий через точку касания, направленный во внешнюю сторону. В 3D графике в основном применяется для реализации освещения и физики.

Нахождение вектора нормали к плоскости, построенной по трем точкам

Пусть даны любые три точки с координатами  ,   и  . Уравнение плоскости, выглядит следующим образом:

Ax + By + Cz + D = 0,

где A, B, C - координаты вектора нормали   к плоскости.

Таким образом можно составить систему уравнений:

Данную систему можно решить с помощью матрицы:

,

определитель которой равен:

Т.к. через любые три точки можно провести плоскость, а количество переменных равно количеству уравнений системы, то имеется хотя бы одно нетривиальное решение системы уравнений (тривиальное решение - A=B=C=D=0). Следовательно, определитель матрицы равен нулю. Таким образом определитель матрицы можно представить в качестве уравнения плоскости, где

,  ,  .

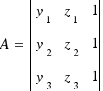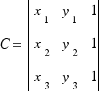Разложив определители получим:

,  ,