1 Вопрос. Матрица. Линейные операции над матрицами. Действия над матрицами.

Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:

Для краткости матрицу можно обозначать одной заглавной буквой, например, А илиВ.

В общем виде матрицу размером m×n записывают так

.

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами a_ij: первый указывает номер строки, а второй – номер столбца. Например, a₂₃ – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Линейные операции с матрицами

Линейными операциями называются операции сложения и умножения на число.

Определение. Суммой двух матриц одинаковой размерности называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых:  .

Определение. Произведением матрицы на число называется матрица той же размерности, каждый элемент которой равен произведению соответствующего элемента на число:  .

ДЕЙСТВИЯ НАД МАТРИЦАМИ

Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a_ij = b_ij. Так есл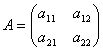и   и  , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

или

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу  или  .

Для любых чисел a и b и матриц A и B выполняются равенства:

1. 

2. 

3. .

2. Определитель 2 –го и n-го порядков. Минор и алгебраическое дополнение.

.Рассмотрим систему двух уравнений с двумя неизвестными:

 (1.7)

Умножим первое уравнение системы на в₂, а второе на в₁, затем вычтем из первого уравнения второе. Получим

(a₁b₂ -a₂b₁) * x = c₁b₂ - c₂b_1.

Подобным образом исключаем х:  (a₁b₂ - a₂b₁) * y = a₁c₂ -a₂c_1. Если

, то

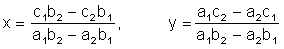. (1.8)

Числитель и знаменатель полученных выражений является определителем второго порядка. Если имеются четыре числа, расположенных в виде квадратной таблицы (матрицы)

,

то определителем (или детерминантом) второго порядка, соответствующим этой таблице, называется число

.

Числа а₁, а₂, в₁, в₂ называются элементами определителя. По аналогии с матрицами элементы а₁,в₂ образуют главную диагональ определителя, а элементы а₂,в₁ - побочную.

Правило. Определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.

Пусть A = (aij)   (i, j = 1, …, n) — квадратная матрица порядка n. Определителем (или детерминантом) матрицы A называется число, которое ставится в соответствие этой матрице и может быть вычислено по ее элементам. Обозначается определитель матрицы A символами

det A    или	п п п п п п	a11 a12 … a1n a21 a22 … a2n … … … … an1 an2 … ann	п п п п п п

Определитель матрицы n×n называется определителем n–го порядка.

Свойства определителя n-го порядка

Свойство 1. При замене строк столбцами (транспонировании) значение определителя не изменится, т.е.

Свойство 2. Если хотя бы один ряд (строка или столбец) состоит из нулей, то определитель равен нулю. Доказательство очевидно.

В самом деле, тогда в каждом члене определителя один из множителей будет нуль.

Свойство 3. Если в определителе поменять местами два соседних параллельных ряда (строки или столбцы), то определитель поменяет знак на противоположный, т.е.

 

Свойство 4. Если в определителе имеются два одинаковых параллельных ряда, то определитель равен нулю:

Свойство 5. Если в определителе два параллельных ряда пропорциональны, то определитель равен нулю:

Свойство 6. Если все элементы определителя, стоящие в одном ряду, умножить на одно и то же число, то значение определителя изменится в это число раз:

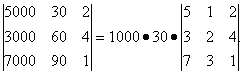
Следствие. Общий множитель, содержащийся во всех элементах одного ряда, можно вынести за знак определителя, например:

 

Свойство 7. Если в определителе все элементы одного ряда представлены в виде суммы двух слагаемых, то он равен сумме двух определителей:

Свойство 8. Если к элементам какого-либо ряда прибавить произведение соответствующих элементов параллельного ряда на постоянный множитель, то значение определителя не изменится:

Свойство 9. Если к элементам i-го ряда прибавить линейную комбинацию соответствующих элементов нескольких параллельных рядов, то значение определителя не изменится:

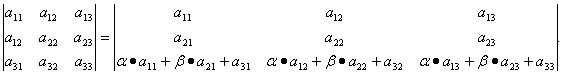
Справедливость этого равенства вытекает из свойства 8.

 

Миноры и алгебраические дополнения.

Определение. Если в определителе n-го порядка выбрать произвольно pстрок и p столбцов (p < n), то элементы, находящиеся на пересечении этих строк и столбцов, образуют матрицу порядка  .

Определитель этой матрицы называется минором исходного определителя. Например, рассмотрим определитель  :

Из строк и столбцов с чётными номерами построим матрицу:

Определитель

называется минором определителя  . Получили минор второго порядка. Ясно, что из    можно построить различные миноры первого, второго и третьего порядка.

Если взять элемент   и вычеркнуть в определителе  строку и столбец, на пересечении которых он стоит, то получим минор, называемый минором элемента  , который обозначим через  :

.

Если минор   умножить на   , где 3 + 2 – сумма номеров строки и столбца, на пересечении которых стоит элемент   то полученное произведение называется алгебраическим дополнением элемента  и обозначается  ,

т.е.

Вообще, минор элемента   будем обозначать  , а алгебраическое дополнение   ,

причём

                  (4)

Для примера вычислим алгебраические дополнения элементов   и   определителя третьего порядка  :

По формуле (4) получим

 

Для вычисления определителя n-го порядка полезно знать следующую теорему: определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения, т.е.

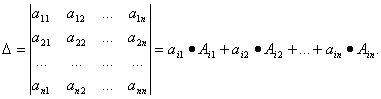(i = 1, 2, ..., n)