
- •2. Основное уравнение молекулярно-кинетической теории идеального газа
- •3.Внутренняя энергия идеального газа. Закон равномерного распределения энергии по степеням свободы.
- •4.Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам
- •5.Адиабатический процесс. Уравнение адиабаты. Политропические процессы.
- •6.Круговой процесс и его кпд. Обратимые и необратимые процессы. Цикл карно. Первая и вторая теоремы карно.
- •7.Энтропия. Второе и третье начала термодинамики. Изменение энтропии в процессах идеального газа.
- •8. Термодинамические потенциалы. Химический потенциал системы, энтальпия, свободная энергия гельмгольца, потенциал гиббса.
- •9.Распределение максвелла по скоростям для молекул идеального газа. Опыт штерна
- •Наиболее вероятная скорость
- •Средняя скорость
- •Среднеквадратичная скорость
- •10.Барометрическая формула. Распределение больцмана.
- •11.Явления переноса (закон фика, закон фурье, закон ньютона). Средняя длина свободного пробега молекулы.
- •12.Реальные газы. Уравнение ван-дер-ваальса и его изотермы.
- •13.Внутренняя энергия реального газа. Эффект джоуля - томсона.
- •14.Фазы вещества. Фазовое равновесие и фазовые переходы 1-го и 2-го рода. Фазовые диаграммы состояния вещества. Тройная точка
- •15.Явления на границе жидкости и твёрдого тела. Капиллярный явления.
- •16.Кристаллические и аморфные твердые тела. Строение и симметрия кристаллов.
- •17.Классическая теория теплоемкости твердых тел. Закон дюлонга и пти.
- •18.Типы кристаллических решеток. Виды связей атомов в кристаллах. Модель эйнштейна и модель дебая.
- •19.Электрический заряд. Свойства электрического заряда. Взаимодействие электрических зарядов. Электрическое поле. Закон кулона.
- •20.Напряженность электрического поля. Силовые линии. Принцип суперпозиции. Напряженность поля точечного заряда и системы точечных зарядов.
- •21.Напряженность электрического поля. Силовые линии. Принцип суперпозиции. Напряженность поля точечного заряда и системы точечных зарядов.
- •22.Поток вектора напряженности электрического поля. Эквипотенциальные поверхности. Теорема гаусса для электростатического поля.
- •23.Применение теоремы гаусса к расчету напряженности электрических полей. Электрическое поле равномерно заряженной сферической поверхности и объемно заряженного шара.
- •25.Связь между напряженностью и потенциалом электростатического поля
- •26.Работа по перемещению заряда в электрическом поле. Разность потенциалов.
- •28.Свободные и связанные заряды в веществе. Электрический диполь. Потенциал и напряженность электрического поля на продолжении оси диполя.
- •28.Свободные и связанные заряды в веществе. Электрический диполь. Потенциал и напряженность электрического поля на продолжении оси диполя.
- •30.Типы диэлектриков. Поляризация диэлектриков. Поляризационные заряды. Вектор поляризации. Напряженность электрического поля в диэлектрике. Диэлектрическая восприимчивость.
- •31.Поляризация полярных и неполярных диэлектриков. Поляризуемость молекулы. Диэлектрическая восприимчивость полярных и неполярных диэлектриков. Ионная поляризация.
- •32.Теорема гаусса для диэлектрического поля в диэлектрике. Вектор электрического смещения.
- •33.Условия на границе двух однородных изотропных диэлектриков. Вектор электрического смещения. Относительная диэлектрическая проницаемость.
- •34.Спонтанная поляризация кристаллических диэлектриков. Сегнетоэлектрики. Пироэлектрики. Пьезоэлектрики.
- •36.Электростатическое поле внутри заряженного проводника и вблизи его поверхности. Проводники во внешнем электростатическом поле. Электроемкость уединенного проводника.
- •37.Конденсаторы. Типы конденсаторов. Соединение конденсаторов. Емкость плоского конденсатора.
- •38.Энергия заряженных проводника и конденсатора энергия электрического поля. Объемная плотность энергии.
- •39.Электрический ток проводимости в металлах, его характеристики и условия существования. Сторонние силы. Электродвижущая сила и напряжение.
- •40.Сопротивление проводников. Закон ома для однородного и неоднородного участков цепи, для замкнутой цепи. Правила кирхгофа.
- •41.Работа и мощность тока. Закон джоуля-ленца в интегральной и дифференциальной формах.
- •42. Основы классической электронной теории электропроводности металлов. Удельная электропроводность. Подвижносъ носителей тока.
- •43.Закон джоуля-ленца, закон видемана-франца и закон ома на основе классической теории электропроводности
- •44.Электрический ток в жидкостях и газах. Законы фарадея для электролиза. Ионизация молекул газов. Электрический ток в газах. Газовые разряды. Электропроводность газов. Плазма.
- •45. Электрический ток в вакууме. Работа выхода электронов из металла. Контактная разность потенциалов. Термоэлектродвижущая сила. Эффекты пельтье и томсона.
- •46. Электрический ток в вакууме. Электронная эмиссия. Виды эмиссий и их применение. Формула
32.Теорема гаусса для диэлектрического поля в диэлектрике. Вектор электрического смещения.
Напряженность
электростатического поля,
 ,
зависит от свойств среды: в
однородной изотропной
среде напряженность поля Е
обратно
пропорциональна
,
зависит от свойств среды: в
однородной изотропной
среде напряженность поля Е
обратно
пропорциональна
 .
Вектор
напряженности
Е, переходя через границу диэлектриков,
претерпевает скачкообразное
изменение, создавая
тем самым неудобства при расчетах
электростатических полей. Поэтому
оказалось
необходимым
помимо вектора
напряженности
характеризовать
поле еще вектором
электрического смещения,
который для
электрически изотропной
среды, по определению, равен
.
Вектор
напряженности
Е, переходя через границу диэлектриков,
претерпевает скачкообразное
изменение, создавая
тем самым неудобства при расчетах
электростатических полей. Поэтому
оказалось
необходимым
помимо вектора
напряженности
характеризовать
поле еще вектором
электрического смещения,
который для
электрически изотропной
среды, по определению, равен
 .
Используя формулы
.
Используя формулы
 и
и
 ,
вектор электрического смещения можно
выразить как
,
вектор электрического смещения можно
выразить как

Единица электрического смещения — кулон на метр в квадрате (Кл/м2).
Теорема
Гаусса для электростатического поля в
диэлектрике:

т.
е. поток вектора смещения электростатического
поля в диэлектрике сквозь произвольную
замкнутую поверхность равен алгебраической
сумме заключенных внутри этой поверхности
свободных электрических зарядов. В
такой форме теорема Гаусса справедлива
для электростатического поля как для
однородной и изотропной, и для неоднородной
и анизотропной сред. Для вакуума

 ,
тогда поток вектора напряженности Е
сквозь произвольную замкнутую поверхность
равен
,
тогда поток вектора напряженности Е
сквозь произвольную замкнутую поверхность
равен
 Так как источниками поля Е в среде
являются как свободные, так и связан
заряды, то теорему Гаусса для поля Е в
самом общем виде можно записать
Так как источниками поля Е в среде
являются как свободные, так и связан
заряды, то теорему Гаусса для поля Е в
самом общем виде можно записать
 где
где
 и
и
 — соответственно алгебраические суммы
свободных и связанных зарядов, охватываемых
замкнутой поверхностью S.
— соответственно алгебраические суммы
свободных и связанных зарядов, охватываемых
замкнутой поверхностью S.
33.Условия на границе двух однородных изотропных диэлектриков. Вектор электрического смещения. Относительная диэлектрическая проницаемость.
Условия на границе раздала двух диэлектрических сред
Р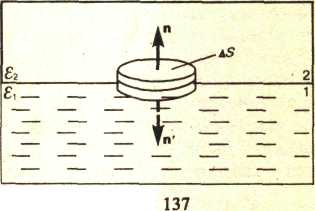 ассмотрим
связь между
векторами Е и
D
на границе раздела двух
однородных изотропных
диэлектриков (диэлектрические
проницаемости которых
ассмотрим
связь между
векторами Е и
D
на границе раздела двух
однородных изотропных
диэлектриков (диэлектрические
проницаемости которых
 и
и
 )
при отсутствии
на границе
свободных
зарядов.
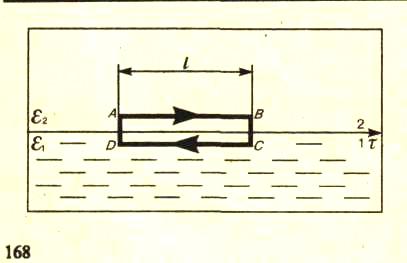
Построим
вблизи
границы раздела диэлектриков 1
и 2 небольшой замкнутый
прямоугольный контур
ABCDA
длины l,
ориентировав его так, как
показано нарис1.
Согласно теореме
)
при отсутствии
на границе
свободных
зарядов.
Построим
вблизи
границы раздела диэлектриков 1
и 2 небольшой замкнутый
прямоугольный контур
ABCDA
длины l,
ориентировав его так, как
показано нарис1.
Согласно теореме о циркуляции вектора Е
о циркуляции вектора Е

Откуда
 (знаки интегралов
по АВ
и CD
разные, так как пути
интегрирования противоположны, а
интегралы по
участкам ВС н
DA
ничтожно малы). Поэтому
(знаки интегралов
по АВ
и CD
разные, так как пути
интегрирования противоположны, а
интегралы по
участкам ВС н
DA
ничтожно малы). Поэтому
 (1)
Заменив, проекции вектора
Е проекциями вектора D, деленными на
(1)
Заменив, проекции вектора
Е проекциями вектора D, деленными на
 ,
получим
,
получим
 На границе раздела двух диэлектриков
(рис.2)
построим прямой цилиндр ничтожно малой
высоты, одно основание которого находится
в первом диэлектрике, другое — во втором.
На границе раздела двух диэлектриков
(рис.2)
построим прямой цилиндр ничтожно малой
высоты, одно основание которого находится
в первом диэлектрике, другое — во втором.
 Основания
AS настолько малы, что в пределах каждого
из них вектор D одинаков. Согласно теореме
Гаусса
Основания
AS настолько малы, что в пределах каждого
из них вектор D одинаков. Согласно теореме
Гаусса
 (нормали
(нормали
 и
и
 к основаниям цилиндра направлены
противоположно). Поэтому
к основаниям цилиндра направлены
противоположно). Поэтому
 Заменив, проекции вектора D проекциями
вектора Е, умноженными на
,
получим (4)
Заменив, проекции вектора D проекциями
вектора Е, умноженными на
,
получим (4) Таким
образом, при переходе через границу
раздела двух диэлектрических сред
тангенциальная
составляющая вектора Е (
Таким
образом, при переходе через границу
раздела двух диэлектрических сред
тангенциальная
составляющая вектора Е ( )
и нормальная составляющая вектора D
(
)
и нормальная составляющая вектора D
( )
изменяются непрерывно (не претерпевают
скачка), а нормальная составляющая
вектора Е (Еn)
и тангенциальная
составляющая вектора D
(Dt)
претерпевают скачок.
)
изменяются непрерывно (не претерпевают
скачка), а нормальная составляющая
вектора Е (Еn)
и тангенциальная
составляющая вектора D
(Dt)
претерпевают скачок.
И з
условий (1) — (4) для составляющих векторов
Е и D
следует, что линии этих
векторов испытывают излом (преломляются).
Найдем связь между углами
з
условий (1) — (4) для составляющих векторов
Е и D
следует, что линии этих
векторов испытывают излом (преломляются).
Найдем связь между углами
 и
и
 (на
рис. 3
>
)
(на
рис. 3
>
)
Согласно
(1) и (4),
и
 Разложим векторы E1
и Е2
у границы раздела на
тангенциальные и нормальные составляющие.
Из рис.3 следует, что
Разложим векторы E1
и Е2
у границы раздела на
тангенциальные и нормальные составляющие.
Из рис.3 следует, что
 Учитывая записанные выше условия,
получим закон преломления линий
напряженности Е (а значит, и линий
смещения D)
Учитывая записанные выше условия,
получим закон преломления линий
напряженности Е (а значит, и линий
смещения D)
 Эта формула показывает, что, входя в
диэлектрик с большой диэлектрической
проницаемостью, линии Е и D
удаляются от нормали.
Эта формула показывает, что, входя в
диэлектрик с большой диэлектрической
проницаемостью, линии Е и D
удаляются от нормали.
Вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для электрически изотропной среды, по определению, равен . Используя формулы и , вектор электрического смещения можно выразить как
Единица электрического смещения — кулон на метр в квадрате (Кл/м2).
Относи́тельная диэлектри́ческая проница́емость среды ε — безразмерная физическая величина, характеризующая свойства изолирующей (диэлектрической) среды. Связана с эффектом поляризации диэлектриков под действием электрического поля (и с характеризующей этот эффект величиной диэлектрической восприимчивости среды). Величина ε показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме
