23.Применение теоремы гаусса к расчету напряженности электрических полей. Электрическое поле равномерно заряженной сферической поверхности и объемно заряженного шара.

Взаимодействие между покоящимися зарядами осуществляется через электрическое поле.

Если все заряды, создающие поле, в данной системе отсчета неподвижны, то поле называется электростатическим.

Электрическое поле – векторное поле, определяющее воздействие на заряженные частицы, не зависящее от их скоростей. Электрическое поле является одной из компонент единого электромагнитного поля.

Поле объемно заряженного шара

Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью r.

Поле равномерно заряженной сферической поверхности

 Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью .

Б лагодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально. Напряженность поля будет, таким образом, одинакова во всех точках воображаемой сферы радиуса r, концентричной с заряженной сферой. Поскольку напряженность поля   перпендикулярна поверхности, теорема Гаусса дает.

24.ПРИМЕНЕНИЕ ТЕОРЕМЫ ГАУССА К РАСЧЕТУ НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ. Теорема Гаусса: Поток вектора напряжённости электрического поля через любую, произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью.

25.Связь между напряженностью и потенциалом электростатического поля

Связь между напряженностью и потенциалом электростатического поля

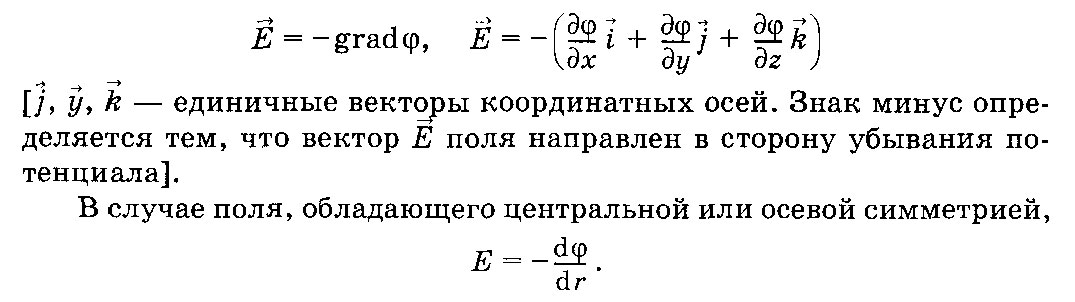
1.Поле равномерно заряженной бесконечной плоскости задается формулой: E=σ/(2ε0), где σ — поверхностная плотность заряда. Разность потенциалов между точками, которые лежат на расстояниях x1 и х2 от плоскости, равна (используем формулу Ex = -∂φ/∂x) 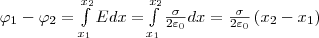   2. Поле двух бесконечных параллельных разноименно заряженных плоскостей задается формулой: Е=σ/ε0, где σ — поверхностная плотность заряда. Разность потенциалов между плоскостями, ежду которыми расстояние равно d (используем формулу Ex = -∂φ/∂x), равна    3. Поле равномерно заряженной сферической поверхности радиуса R с общим зарядом Q вне сферы  (r>R) задается формулой: (4πε0)-1(Q/r2) разность потенциалов между двумя точками, лежащими на расстояниях r1 и r2 от центра сферы (r1>R, r2>R, r2>r1), равна   

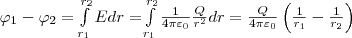
26.Работа по перемещению заряда в электрическом поле. Разность потенциалов.

Разные заряды в точке с координатой х обладают разной потенциальной энергией. Однако, отношение значения потенциальной энергии к величине соответствующего заряда есть величина постоянная, равная величине потенциальной энергии единичного заряда, находящегося в данной точке поля. Эта величина называется потенциалом поля в данной точке:             

 Потенциал φ является энергетической характеристикой электростатического поля.

Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек: 

A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2).

  В Международной системе единиц (СИ) единицей потенциала является вольт (В). 1 В = 1 Дж / 1 Кл.

В о многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

    Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Циркуляция вектора напряженности электрического поля. Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:

Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.

 .

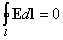Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле – потенциальным.

,