1. СПОСОБЫ ОПИСАНИЯ СОСТОЯНИЯ МИКРОСКОПИЧЕСКОЙ СИСТЕМЫ. ТЕРМОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ СИСТЕМЫ. ИДЕАЛЬНЫЙ ГАЗ, ЗАКОНЫ ИДЕАЛЬНОГО ГАЗА.

Термодинамической  системой  называется совокупность макроскопических тел, состоящих из огромного числа независимо движущихся молекул (материальных точек). Под телом может подразумеваться и жидкость, и газ, и кристалл, и плазма и т.д.

Следовательно, термодинамическая система --- это система с огромным числом степеней свободы. Описать ее можно с помощью микроскопических параметров, т.е. скоростей, координат, масс отдельных молекул. Тогда изменение состояния системы, т.е. процесс, протекающий в ней, будет суммарным результатом движения всех молекул. Такой способ описания называется молекулярно--кинетическим или статистическим

Но можно описать термодинамическую систему, не интересуясь движением отдельных молекул, т.е. с помощью макроскопических или термодинамических параметров, характеризующих состояние системы в целом. Такими параметрами являются: объем V, давление p, температура T, поляризованность  , намагниченность   и т.п. Этот способ описания называется термодинамическим и изучается в термодинамике.

Если значения всех термодинамических параметров одинаковы во всех точках термодинамической системы и неизменны во времени, то она называется равновесной, а состояние такой системы - равновесным состоянием.    Если же значения хотя бы одного термодинамического параметра различны в разных точках системы или он изменяется во времени, то ее состояние называется неравновесным.   Процесс перехода системы из неравновесного в равновесное состояние называется релаксацией, а время, за которое устанавливаются равновесные значения всех параметров системы, - временем релаксации t

Равновесное состояние системы можно изобразить точкой на диаграмме состояний в координатах p, V; p, T или T, V  (неравновесное состояние задать на диаграмме состояний нельзя, так как термодинамические параметры для системы различны в разных точках).

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией .Уравнение состояния в этой форме называют уравнением Клапейрона–Менделеева.

где М – масса газа, а μ – масса одного моля (молярная масса).

1. При постоянной температуре и массе из следует, что  , т.е. при постоянной температуре и массе газа его давление обратно пропорционально объему. Этот закон называется законом Бойля и Мариотта, а процесс, при котором температура постоянна, называется изотермическим.

2. Для изобарного процесса, происходящего при постоянном давлении, , т.е. объем пропорционален абсолютной температуре. Этот закон называют законом Гей-Люссака.

3. Для изохорного процесса, происходящего при постоянном объеме , т.е. давление пропорционально абсолютной температуре. Этот закон называют законом Шарля.

2. Основное уравнение молекулярно-кинетической теории идеального газа

Молекулярно-кинетическая теория (сокращённо МКТ) — теория, рассматривавшая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:

-все тела состоят из частиц: атомов, молекул и ионов;

-частицы находятся в непрерывном хаотическом движении (тепловом);

-частицы взаимодействуют друг с другом путём абсолютно упругих столкновений. Основное уравнение МКТ

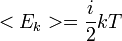, где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро NA), i — число степеней свободы молекул (  в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура.

Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) 

где  — давление,  — молярный объём,  — универсальная газовая постоянная  — абсолютная температура,К.

Так как 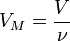 , где   — количество вещества, а 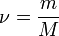 , где   — масса,   — молярная масса, уравнение состояния можно записать:

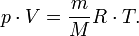
Изопроцессы — равновесные процессы, в которых один из основных параметров сохраняется.

И 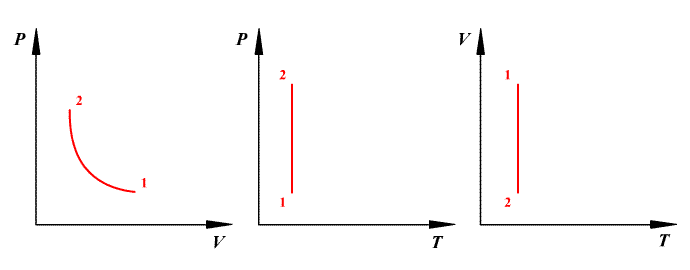ЗОБАРНЫЙ ПРОЦЕСС ( ) Для изобарного процесса в идеальном газе справедлив закон Гей-Люссака: при постоянном давлении объем данной массы газа прямо пропорционален его термодинамической температуре:  или  .   ИЗОХОРНЫЙ ПРОЦЕСС ( ) Изохорный процесс в идеальном газе описывается законом Шарля: при постоянном объеме давление данной массы газа прямо пропорционально его термодинамической температуре:  или  .   ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС ( ) Изотермический процесс в идеальном газе подчиняется закону Бойля - Мариотта: для данной массы газа при неизменной температуре произведение значений давления и объема есть величина постоянная:  или  .  

3.Внутренняя энергия идеального газа. Закон равномерного распределения энергии по степеням свободы.

В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна

,

Средняя энергия приходящаяся на одну степень свободы:

У одноатомной молекулы i = 3, тогда для одноатомных молекул

для двухатомных молекул

для трёхатомных молекул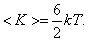

Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится

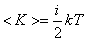
Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы.

4.Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам

Тепло  , полученное системой, идет на изменение ее внутренней энергии    и совершение работы над внешними телами  : . Первое начало термодинамики — это закон сохранения и превращения энергии применительно к термодинамическим процессам. Работа внешних тел над системой 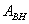   связана с работой системы над внешними телами    соотношением:  .

Работа газа при изобарическом расширении (при расширении с постоянным давлением): .

Изохорный процесс (V=const). Диаграмма этого процесса (изохора, где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.   Из первого начала термодинамики (δQ=dU+δA) для изохорного процесса следует, что вся теплота, которая сообщается газу, идет на увеличение его внутренней энергии:   

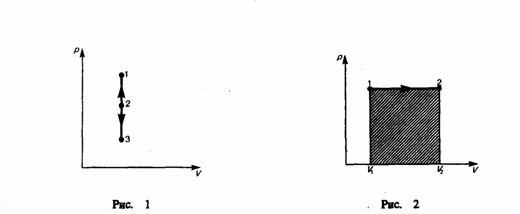
Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, которая параллельна оси V. При изобарном процессе работа газа при увеличения объема от V1 до V2 равна 

Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля—Мариотта:   Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, которая расположена на диаграмме тем выше, чем выше температура, при которой происходит процесс.  Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплотыδQ, полученного телом, к соответствующему приращению его температуры δT:

Единица измерения теплоёмкости в системе СИ — Дж/К.

   Из основного уравнения молекулярно-кинетической теории  . При изобарическом процессе Р = const. Следовательно, получим: С_Р – теплоемкость при постоянном давлении. 

      Это уравнение Майера для одного моля газа.   Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.