Уравнением с разделяющимися переменными.

Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:

где p(x) и h(y) − непрерывные функции.  Рассматривая производную y' как отношение дифференциалов  , перенесем dx в правую часть и разделим уравнение на h(y):

Разумеется, нужно убедиться, что h(y) ≠ 0. Если найдется число x₀, при котором h(x₀) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.  Обозначив  , запишем уравнение в форме:

Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:

где C − постоянная интегрирования.  Вычисляя интегралы, получаем выражение

описывающее общее решение уравнения с разделяющимися переменными.

2.Дифференциальные уравнения с разделенными переменными

Рассмотрим дифференциальное уравнение вида:

f1(x)dx=f2(y)dy,     (1)

которое называется уравнением с разделенными переменными. Пусть найдено некоторое его решение y(x). При подстановке y=y(x) в дифференциальное уравнение (1) оно обратится в тождество и, интегрируя его, имеем

∫f1(x)dx=∫f2(y)dy+C,    (2)

3.Однородные дифференциальные уравнения первого порядка

Однородным дифференциальным уравнением первого порядка, называется уравнение, имеющее вид

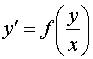   (7)

Подстановка 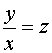 ;  ;  , где   преобразует это уравнение к уравнению с разделяющимися переменными.

  ,

  ,

  .

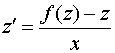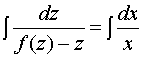2. 4. Линейные уравнения первого порядка и уравнения Бернулли

Дифференциальное уравнение первого порядка называется линейным, если оно содержит  и  в первой степени, то есть имеет вид  .

Уравнением Бернулли называется дифференциальное уравнение первого порядка вида  , где  и  .

Эти уравнения решают с помощью подстановки  .

Пример 3. Решить уравнение  .

Решение. Это уравнение является уравнением Бернулли. Решим это уравнение с помощью подстановки  . Тогда  . Подставляя  и  в уравнение, получим:  . Преобразуем это уравнение к виду  . Найдем функцию  , полагая в последнем уравнении . Тогда       (мы нашли одну из первообразных функции  ). Подставляя найденную функцию  в уравнение относительно  и , получим   или  .

Разделяем переменные и находим функцию  :

Возведя  в квадрат, находим

Определение уравнения в полных дифференциалах

Дифференциальное уравнение вида

называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение

Общее решение уравнения в полных дифференциалах определяется формулой

где C − произвольная постоянная.

Алгоритм решения уравнения в полных дифференциалах

1. Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:

           

2. Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):

           

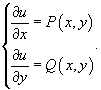
3. Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:

           

4. Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:

           

Отсюда получаем выражение для производной неизвестной функции φ(y):

           

5. Интегрируя последнее выражение, находим функцию φ(y) и, следовательно, функцию u(x,y):

           

6. Общее решение уравнения в полных дифференциалах записывается в виде:

           

7.Дифференциальные уравнения высших порядков.

  Определение. Дифференциальным уравнением порядка n называется уравнение вида:

 В некоторых случаях это уравнение можно разрешить относительно y⁽ⁿ⁾:

 Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений.

 

  Определение. Решение  удовлетворяет начальным условиям  , если 

 

  Определение. Нахождение решения уравнения  , удовлетворяющего начальным условиям  , называется решением задачи Коши.

  Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).

  Если функция (n-1) –й переменных вида  в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по  , то какова бы не была точка ( ) в этой области, существует единственное решение   уравнения  , определенного в некотором интервале, содержащем точку х₀, удовлетворяющее начальным условиям  .

 

  Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.

  Рассмотрим подробнее методы нахождения решений этих уравнений.