Курс лекций по математике элементы дискретной математики Лекция 3 Построение минимальных днф с помощью карт Карно. Алгоритм Квайна- Мак-Клоски

3.1 Минимальные днф

СДНФ, которая строится по таблице булевой функции, зачастую оказывается весьма сложной, т.е. она содержит достаточно много элементарных конъюнкций и литералов. При решении некоторых задач (например, минимизация схем) необходимо уметь находить в определенном смысле минимальную ДНФ, представляющую данную функцию.

ДНФ называют минимальной, если она содержит наименьшее число литералов, среди всех ДНФ, эквивалентных ей.

Пример: ДНФ x₁x₂ + ¬ x₁x₂ не является минимальной, так как ее можно преобразовать к эквивалентной ДНФ:

x₁x₂ + ¬ x₁x₂ = x₂( x₁ + ¬ x₁) = x₂▪ 1 = x₂.

Вместо четырех литералов в исходной ДНФ получаем ДНФ, состоящую из одного литерала.

Длиной ДНФ называют число входящих в нее элементарных конъюнкций.

ДНФ называют кратчайшей, если она имеет наименьшую длину среди всех эквивалентных ей ДНФ.

Заметим, что кратчайшая ДНФ не обязана быть в то же время минимальной среди всех ДНФ, эквивалентных исходной функции. Но поиск минимальных ДНФ проводится среди кратчайших ДНФ.

3.2 Алгоритм Квайна – Мак-Клоски

Наша задача состоит в том, чтобы описать метод построения минимальной ДНФ, эквивалентной заданной булевой функции. Мы рассмотрим простейший метод такого рода, основанный на алгоритме Квайна – Мак-Клоски. Этот алгоритм исходит обязательно из СДНФ, которая строится по таблице функции так, как это было описано в предыдущей лекции (2.5).

Опишем последовательно этапы, составляющие алгоритм Квайна – Мак-Клоски.

3.2.1 Склейка

Пусть К₁ и К₂ – две элементарные конъюнкции, входящие в исходную СДНФ, причем для некоторой переменной х и некоторой элементарной конъюнкции К выполняются равенства: К₁ = хК, К₂ = ¬хК. Тогда, согласно тождествам булевой алгебры, имеем:

К₁ + К₂ = хК + ¬хК = К(х + ¬х) = К.

Мы получаем элементарную конъюнкцию К, которая содержит на один литерал меньше, чем К₁ и К₂. Образно говоря, мы "склеили" две конъюнкции в одну, в которой число литералов на единицу меньше.

Установим геометрический смысл простой склейки с точки зрения "геометрии" булева куба. Простая склейка может быть применена только к таким двум элементарным конъюнкциям K_a и K_b, соответствующим наборам переменных a и b, что для некоторого i

a = (a₁, a₂,..., a _{i – 1}, a _i, a _{i + 1}, …, a_n),

b = (a₁, a₂,…, a _{i – 1}, ¬a _i, a _{i + 1}, …, a_n).

Это значит, что наборы a и b таковы, что один из них доминирует над другим (они различаются значением только одной компоненты, значит a ≤ b или b ≤ a), т.е. они образуют ребро булева куба Вⁿ. Следовательно, простой склейке, применяемой к элементарным конъюнкциям исходной СДНФ, представляющей функцию, подлежат те и только те элементарные конъюнкции, которые соответствуют элементам какого-либо ребра булева куба, на котором функция принимает единичное значение. Образно говоря, две соседние вершины куба, на которых функция равна 1, "склеиваются" в ребро, их "соединяющее".

Пример: Зададим функцию от трех переменных следующей СДНФ:

f = ¬x₁ ¬x₂ ¬x₃ + ¬x₁ ¬x₂ x₃ + x₁ ¬x₂ ¬x₃ + x₁ ¬x₂ x₃.

Подвергнем простой склейке первую и третью, а также вторую и четвертую элементарные конъюнкции:

f = ¬x₂ ¬x₃ + ¬x₂ x₃.

С геометрической точки зрения склейка первой и третьей конъюнкций означает, что функция f принимает единичное значение на ребре [000, 100] (рисунок 3.1), а склейка второй и четвертой конъюнкций точно также определяет ребро [001, 101]. Эти ребра являются соседними, и, кроме того, оказывается, что функция f принимает единичное значение и на другой паре соседних ребер: [000, 001], [100, 101]. Здесь сказывается существенное отличие "геометрии" булева куба от классической: в булевом кубе ребро – это пара вершин, между которыми нет никаких "точек". Тогда любая пара соседних ребер образует грань размерности 2, любая пара соседних граней размерности 2 образует грань размерности 3 и т.д. Таким образом, если функция принимает единичное значение на двух соседних ребрах булева куба, то она равна 1 в любой точке образуемой ими грани размерности 2, если она равна 1 на двух параллельных соседних гранях размерности 2, то она равна 1 на соответствующей грани размерности 3 и т.д. Применяя простую склейку по переменной x₃, получим:

f = ¬x₂.

Побочным результатом склейки явилось удаление фиктивных переменных функции x₁ и x₃.

Для булевых функций от трех и четырех переменных процедура склейки наглядно и просто выполняется на так называемых картах Карно. Форма карт Карно, представляющих собой прямоугольные таблицы, для функции от трех переменных показана на рисунке 3.2, а для функции от четырех переменных – на рисунке 3.3. На рисунке 3.2 строки отмечены наборами значений переменной х₁, а столбцы – х₂, х₃; а на рисунке 3.3 строки – наборами значений переменных х₁, х₂, а столбцы – х₃, х₄.

х2х3 х1	00	01	11	10
0
1

Рисунок 3.2

х3х4 х1х2	00	01	11	10
00
01
11
10

Рисунок 3.3

Карта Карно есть не что иное, как форма таблицы для определения булевой функции. Каждая клетка карты задается своим набором значений переменных. Единичные значения функции проставляются в соответствующие клетки, клетки, соответствующие нулевому значению функции, остаются пустыми. Карта Карно устроена так, что наборы, определяющие любые две соседние клетки, различаются в точности в одной позиции (т.е. различаются значениями ровно одной компоненты), причем клетки одной и той же строки или одного и того же столбца, примыкающие к противоположным сторонам прямоугольника, также являются соседними в только что определенном смысле. Это можно представить себе так, что карта "закручивается" в "цилиндр" по обоим направлениям, т.е. в "тор". С геометрической точки зрения карта Карно есть способ изображения булева куба.

Пусть булева функция f задана таблицей, представленной в виде карты Карно. Описанный выше процесс склейки, в результате которого получается сокращенная ДНФ функции f проводится на карте Карно так: любые две соседние клетки, содержащие единицы, обводятся, и "поглотивший" их прямоугольник (он и есть результат обозначения склейки на карте) представляется словом, содержащим "0", "1" и символ "×" ("крестик"), причем "крестик" занимает позицию того переменного, по которому произведена склейка (рисунок 3.4).

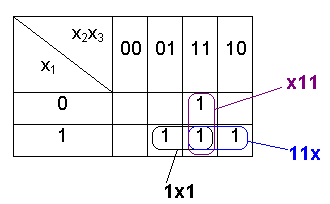
Рисунок 3.4

С геометрической точки зрения такой прямоугольник площади 2 соответствует ребру булева куба, в каждой вершине которого функция принимает значение 1. Запись прямоугольника в виде слова можно понимать как обозначение соответствующего ребра. Так, на карте на рисунке 3.4 прямоугольник 11х обозначает ребро [110, 111], прямоугольники же 1х1 и х11 – ребра [101, 111] и [011, 111] соответственно.

По таким обозначениям легко получить и ту конъюнкцию, которая является результатом простой склейки: для этого достаточно записать x _i, если в i – той позиции стоит 1, ¬ x _i, если в i – той позиции стоит 0, и пропустить x _i, если в i – той позиции стоит х ("крестик"). Так, по слову 1х0 получаем конъюнкцию х₁¬х₃ ( ).

Наличие на карте Карно двух прямоугольников площади 2, находящихся в соседних столбцах или строках, показывает, что функция принимает значение 1 на некоторой паре соседних ребер, т.е. на некоторой грани размерности 2. Тогда они могут быть объединены в один большой прямоугольник площади 4 (рисунок 3.5).

Р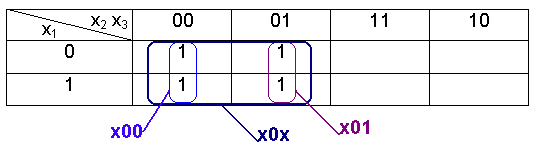 исунок 3.5

Этот прямоугольник можно записать в виде слова х0х, показывая тем самым, что соответствующая грань (размерности 2) образована любой из двух пар соседних ребер: [х00, х01] (два вертикальных прямоугольника площади 2) или [00х, 10х] (два горизонтальных прямоугольника площади 2).

Точно также можно объединять в один прямоугольник площади 8 два соседних прямоугольника площади 4 (рисунок 3.6).

Рисунок 3.6

Если такие большие прямоугольники находить сразу, то "поглощаемые" ими меньшие прямоугольники уже не рассматриваются. Тем самым, находя на карте Карно прямоугольники максимальной площади и не содержащиеся друг в друге, мы находим грани максимальных размерностей и максимальные по включению, такие, на которых заданная функция принимает единичное значение. Поскольку грань размерности k имеет 2^k вершин, то выделяемые прямоугольники могут состоять только из 2^k клеток (для некоторого k, не превышающего числа переменных). Так, на карте, приведенной на рисунке 3.7, получим два прямоугольника площади 4: х0х0 и 0х0х, соответствующие граням размерности 2, и один прямоугольник 01х1, отвечающий ребру, которое не содержится ни в одной из указанных выше граней. Подчеркнем еще раз, что соседство клеток, прямоугольников и само выделение прямоугольников на карте Карно производится с учетом ее "закрученности". В этой связи интересен "прямоугольник" на карте (рисунок 3.7), обозначенный х0х0. Он образован двумя парами противоположных угловых клеток.

Таким образом, если на карте Карно сразу выделять все прямоугольники максимальных площадей, то тем самым мы "геометрически"

Рисунок 3.7

реализуем описанный ранее процесс склейки и в результате получаем все конъюнкции исходной функции, составляющие сокращенную ДНФ. Эти конъюнкции восстанавливаются по записям прямоугольников. Так, для карты, приведенной на рисунке 3.7, получим сокращенную ДНФ в виде: ¬x₂¬x₄ + ¬x₁¬x₃ + ¬x₁x₂x₄.