12.Нормаль прямой

Здесь p - длина перпендикуляра, опущенного из начала координат на прямую, измеренная в единицах масштаба, а - угол, который этот перпендикуляр образует с положительным направлением оси Ox. Отсчитывается этот угол от оси Ox против часовой стрелки. Для приведения общего уравнения прямой (2) к нормальному виду обе его части надо умножить на нормирующий множитель: (5) причем перед дробью следует выбрать знак, противоположный знаку свободного члена C в общем уравнении прямой (2). Особенности нормального уравнения прямой: сумма квадратов коэффициентов при текущих координатах равна единице, свободный член отрицателен, а правая его часть равна нулю.

13. Вычисление угла между прямыми.

Вычисление угла между прямыми.

Задача вычисления угла между двумя прямыми в пространстве решается так же, как и на плоскости (§ 32). Обозначим через φ величину угла между прямыми l₁ и  l₂, а через ψ — величину угла между направляющими векторами а и b  этих  прямых.

Тогда, если

ψ <90° (рис. 206, а), то φ = ψ; если же ψ > 90° (рис. 206,6), то φ = 180° — ψ. Очевидно, что в обоих случаях верно равенство cos φ = |cos ψ|. По формуле (1) § 20 имеем

следовательно,

Пусть прямые заданы своими каноническими уравнениями

Тогда угол φ между прямыми определяется с помощью формулы

         (1)

Если одна из прямых  (или обе) задана не каноничecкими уравнениями, то для вычисления угла нужно найти координаты направляющих векторов этих прямых, а затем воспользоваться формулой (1).

15. Плоскость в пространстве: общее уравнение; уравнение в отрезках; уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору; уравнение плоскости, проходящей через три данные точки

Общее уравнение плоскости

Пусть в трехмерном пространстве задана прямоугольная декартова система координат.

Общим уравнением плоскости в пространстве называется уравнение вида

Ax + By + Cz + D = 0,

где A2 + B2 + C2 ≠ 0 .

В трехмерном пространстве в декартовой системе координат любая плоскость описывается уравнением 1–ой степени (линейным уравнением). И обратно, любое линейное уравнение определяет плоскость.

Уравнение плоскости в отрезках 

где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Сформулируем следующую задачу:

Составить уравнение плоскости, проходящей через данную точку M(x0,  y0,  z0) перпендикулярно данному вектору 

→

n= {A, B, C} .

Решение. Пусть P(x, y, z) — произвольная точка пространства. Точка P принадлежит плоскости тогда и только тогда, когда вектор MP = {x − x0, y − y0, z − z0} ортогонален вектору 

→

n = {A, B, C}

(рис.1).

Написав условие ортогональности этих векторов (

→

n

, MP) = 0 в координатной форме, получим:

A(x − x0) + B(y − y0) + C(z − z0) = 0

(1)

Это и есть искомое уравнение. Вектор 

→

n= {A, B, C} называется нормальным вектором плоскости.

 Таким образом, чтобы написать уравнение плоскости, нужно знать нормальный вектор плоскости и какую–нибудь точку, принаждежащую плоскости.

Если теперь в уравнении (1) раскрыть скобки и привести подобные члены, получим общее уравнение плоскости:

Ax + By + Cz + D = 0 ,

где D = −Ax0 − By0 − Cz0 .

Уравнение плоскости, проходящей через три точки  М0(x0, y0, z0), М1(x1, y1, z1) и М2(x2, y2, z2), не лежащие на одной прямой, имеет вид

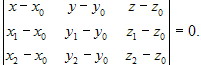
       Параметрическое уравнение.Так же, как для прямой, условие (5.3.1) может быть переписано в виде 

r = r0 + up1 + v2,      u, v ∈ R,        (5.3.3)

или, в координатной форме, в системе координат Oxyz 

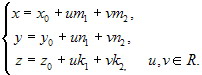                   (5.3.4)

        Уравнения (5.3.3), (5.3.4) называются параметрическими уравнениями плоскости в векторной и координатной формах. 

16. Нормаль плоскости.

Нормаль

Нормаль - это перпендикуляр к касательной прямой или плоскости, проходящий через точку касания, направленный во внешнюю сторону. В 3D графике в основном применяется для реализации освещения и физики.

Нахождение вектора нормали к плоскости, построенной по трем точкам

Пусть даны любые три точки с координатами  ,   и  . Уравнение плоскости, выглядит следующим образом:

Ax + By + Cz + D = 0,

где A, B, C - координаты вектора нормали   к плоскости.

Таким образом можно составить систему уравнений:

Данную систему можно решить с помощью матрицы:

,

определитель которой равен:

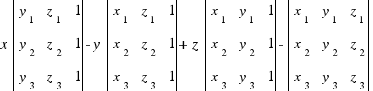
Т.к. через любые три точки можно провести плоскость, а количество переменных равно количеству уравнений системы, то имеется хотя бы одно нетривиальное решение системы уравнений (тривиальное решение - A=B=C=D=0). Следовательно, определитель матрицы равен нулю. Таким образом определитель матрицы можно представить в качестве уравнения плоскости, где

,  ,  .

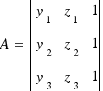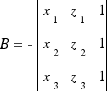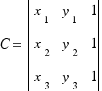Разложив определители получим:

,  ,