2.4. Расчет вала на сложное сопротивление

_{Для расчета был выбран} III вал. Линейные размеры вала и расположение зубчатых колес определим из эскизного проектирования. Схема нагружения вала изображена на рис. 9. На вал III действуют окружные Р_τ и радиальные Р_r усилия от зубчатого зацепления.

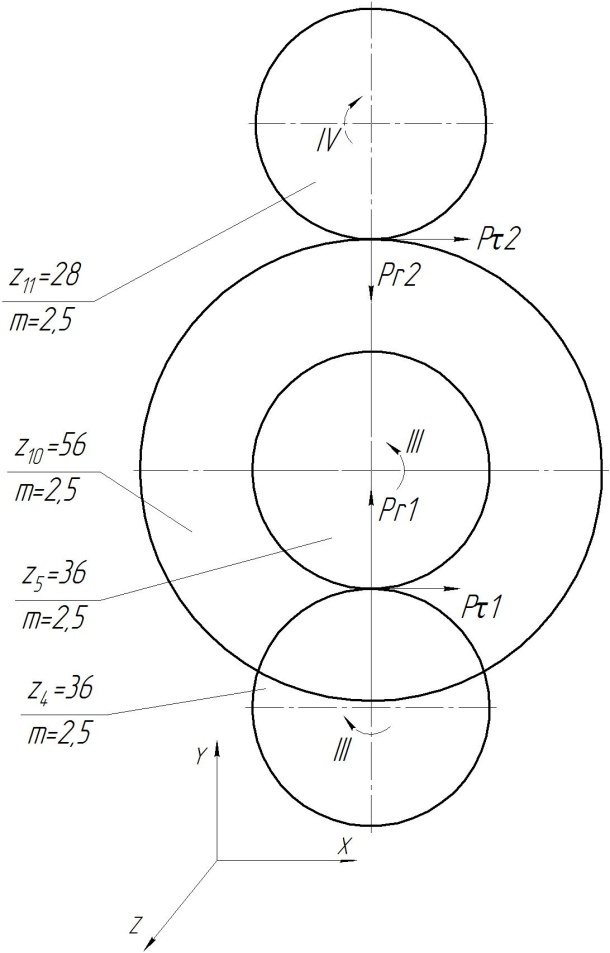
Рис. 9 Расчетная схема действия сил в зубчатых зацеплениях.

Исходя из компоновки, имеем 6 вариантов нагружения вала:

Z₄:Z₅ + Z₁₀:Z₁₁

Z₄:Z₅ + Z₁₂:Z₁₃

Z₆:Z₇ + Z₁₀:Z₁₁

Z₆:Z₇ + Z₁₂:Z₁₃

Z₈:Z₉ + Z₁₀:Z₁₁

Z₈:Z₉ + Z₁₂:Z₁₃

Для расчета выберем первый вариант Z₄:Z₅ + Z₁₀:Z₁₁.

Расчет крутящих моментов 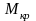возьмем из ориентировочного расчета вала.

Тангенциальная сила действующая в зацеплении:

;

;

Радиальная сила действующая в зацеплении:

;

;

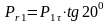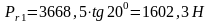Тангенциальная сила действующая в зацеплении:

;

Радиальная сила действующая в зацеплении:

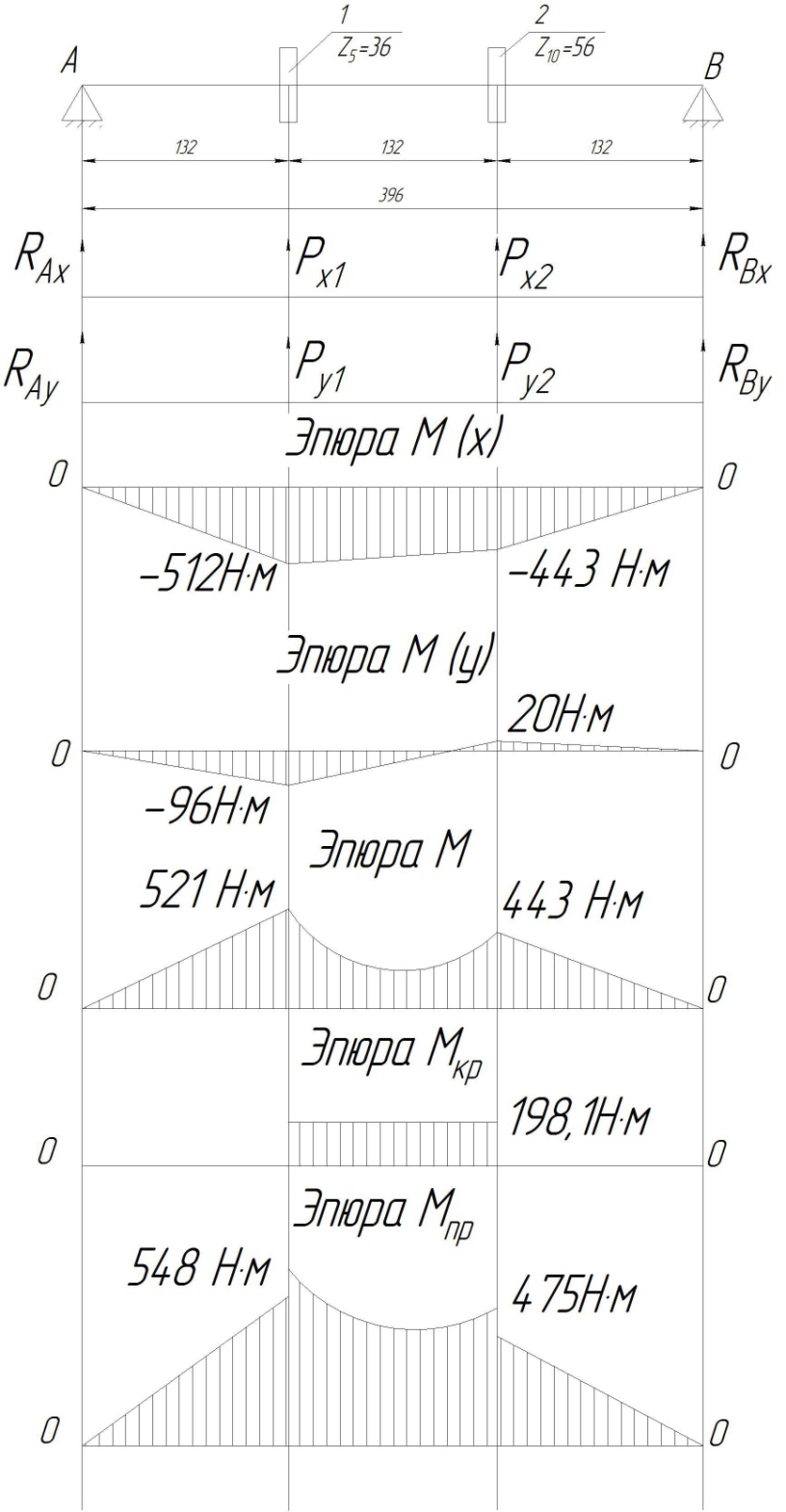
_{Рис. 10. Расчетная схема и результаты расчетов для} первого варианта нагружения III вала.

Проецируем найденные силы на оси ox и oy:

в сечении I:

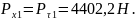
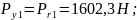
в сечении II:

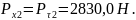
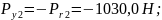
Определение реакций опор в плоскости zox и zoy:

∑m_А(F_х) = 0,

P_x1·132 + P_x2·264+ R_Bx ·396=0,

R_Bx= - (P_x1·132 + P_x2·264)/396= -3354,0 H.

∑m_В(F_х) = 0,

- R_Аx·396 -P_x1 ·264 - P_x2·132 = 0,

R_Аx = - (P_x1 ·264 + P_x2·132)/396= - 3878,2H.

Проверка:

R_Аx + P_x1+P_x2+R_Bx = 0,

-3878,2+4402,2+2830,0-3354,0=0

Реакции в плоскости zox определены правильно.

∑m_А(F_у) = 0,

P_y1·132 + P_y2·264+ R_By ·396 = 0,

R_By= - (P_y1·132 + P_y2·264)/396 = 152,5 H.

∑m_B(F_у) = 0,

- R_Аy·396 –P_y1 ·264 – P_y2·132 = 0,

R_Аy = - (P_y1 ·264 + P_y2·132)/396= -724,8 Н.

Проверка:

R_Аy + P_y1 +P_y2 + R_By = 0,

-724,8 + 1602,3 -1030,0+152,5= 0,

Реакции в плоскости zoу определены правильно.

Расчет изгибающего момента в плоскости zox:

М_и(х₁) = R_Ax · a = - 511,9 H·м,

М_и(х₂) = R_Bx · c = - 442,7 H·м,

Расчет изгибающего момента в плоскости zoу:

М_и(у₁)= R_Ay · a = - 95,7 H·м,

М_и(у₂) = R_By · c = 20,1 H·м.

Расчет суммарного изгибающего момента:

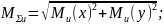
Расчет крутящего момента для III вала:

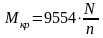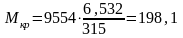, Н·м;

Н·м;

Расчет приведенного момента:

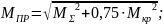
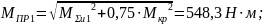
По полученным значениям построим эпюры моментов: М_Х, М_У, М_Σ, М_КР, М_ПР.

Определение диаметра вала в опасном сечении:

;

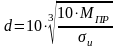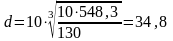мм;

Проверку первого и расчет остальных вариантов зацеплений ведем в Excel (таблица 5).

Таблица 5

Данные:
Варианты зацепленний	Z1	Z2	Mкр	m	L	a	b	c	α	β	Mкр	σи
1	36	56	198,1	2,5	396	132	132	132	0	0	198,1	130
2	36	24	198,1	2,5	396	132	229	35	0	0	198,1	130
3	40	56	198,1	2,5	396	35	229	132	0	0	198,1	130
4	40	24	198,1	2,5	396	35	326	35	0	0	198,1	130
5	44	56	198,1	2,5	396	229	35	132	0	0	198,1	130
6	44	24	198,1	2,5	396	229	132	35	0	0	198,1	130

	Расчет:
Варианты зацепленний	Pτ1	Pτ2	Pr1	Pr2	Px1	Px2	Py1	Py2	RAx	RBx	ΣRx
1	4402	2830	1602	1030	4402	2830	1602	-1030	-3878	-3354	0
2	4402	6603	1602	2403	4402	6603	1602	-2403	-3518	-7487	0
3	3962	2830	1442	1030	3962	2830	1442	-1030	-4555	-2237	0
4	3962	6603	1442	2403	3962	6603	1442	-2403	-4195	-6370	0
5	3602	2830	1311	1030	3602	2830	1311	-1030	-2462	-3970	0
6	3602	6603	1311	2403	3602	6603	1311	-2403	-2103	-8103	0

	Расчет:
Варианты зацепленний	RAy	RBy	ΣRy	Mиx1	Mиx2	Mиy1	Mиy2	Mи1	Mи2	Мпр1	Мпр2	d
1	-725	152,5	0	-512	-443	-95,7	20,14	520,8	443,2	548,3	475,2	34,8
2	-856	1657	0	-464	-262	-113	57,99	478	268,4	507,8	318,5	33,9
3	-971	559,2	0	-159	-295	-34	73,82	163	304,4	236,7	349,4	30,0
4	-1102	2064	0	-147	-223	-38,6	72,22	151,8	234,4	229,1	290,4	28,2
5	-210	-71,4	0	-564	-524	-48	-9,43	565,9	524,1	591,3	551,4	35,7
6	-340	1433	0	-481	-284	-78	50,15	487,8	288	517,1	335,2	34,1

Самые высокие нагрузки возникают на 5 варианте нагружения, минимальный диаметр третьего вала равен 36 мм. Диаметр вала III взят с запасом d=40мм. Следовательно, он способен выдержать возникающие нагрузки.