Понятие алгоритма

В основу работы ЭВМ положен программный принцип управления, состоящий в том, что ЭВМ выполняет действия по заранее заданной программе. Программа – это упорядоченная последовательность команд, которые понимает ЭВМ.

В основе любой программы лежит алгоритм. Алгоритм – это полное и точное описание на некотором языке конечной последовательности правил, указывающих исполнителю действия, которые он должен выполнить, чтобы за конечное время перейти от (варьируемых) исходных данных к искомому результату.

Свойства, которыми должен обладать алгоритм, адресуемый к исполнению на ЭВМ:

1. Первым свойством алгоритма является дискретный (пошаговый) характер определяемого им процесса.

2. Исполнитель может выполнить алгоритм, если он ему понятен, то есть записан на понятном ему языке и содержит предписания, которые исполнитель может выполнить. Набор действий, которые могут быть выполнены исполнителем, называется системой команд исполнителя.

3. Алгоритмы, предназначенные для исполнения техническим устройством, не должны содержать предписаний, приводящих к неоднозначным действиям.

4. Основополагающим свойством алгоритма является его массовость, применимость к некоторому классу объектов, возможность получения результата при различных исходных данных на некоторой области допустимых значений.

5. Цель выполнения алгоритма – получение конечного результата посредством выполнения указанных преобразований над исходными данными.

6. Если алгоритм должен быть выполнен не просто за конечное время, а за разумное конечное время, то речь идет об эффективности алгоритма. Понятие эффективности алгоритма включает такие аспекты, как сложность, необходимые ресурсы, информационно-программное обеспечение.

Алгоритмизация – процесс разработки и описания алгоритма решения какой-либо задачи.

Непосредственная разработка алгоритма начинается с осознания существа поставленной задачи, с анализа того, что нам известно, что следует получить в качестве результата, в какой форме нужно представить исходные данные и результаты вычислений. Следующая ступень – разработка общей идеи алгоритмического процесса и анализа этой идеи. После этого можно приступить к более детальной разработке уже задуманного конкретного алгоритма. И вот этот процесс разработки конкретного алгоритма, в соответствии с определением самого понятия «алгоритм», заключается в последовательном выполнении следующих пунктов:

1) разложении всего вычислительного процесса на отдельные шаги;

2) установлении взаимосвязей между отдельными шагами алгоритма и порядка их следования, приводящего от известных исходных данных к искомому результату;

3) полном и точном описании содержания каждого шага алгоритма на языке выбранной алгоритмической системы;

4) проверке составленного алгоритма на предмет, действительно ли он реализует выбранный метод и приводит к искомому результату.

Два алгоритма эквивалентны если выполняются следующие условия:

1) множество допустимых исходных данных одного из них является множеством допустимых исходных данных и другого;

2) применение этих алгоритмов к одним и тем же исходным данным дает одинаковые результаты.

Лингвистическая и металингвистическая хрень.

Лингвистический знак—это единственное обозначение информационного элемента.

Лингвистическая форма—форма расположения лингвистических знаков, выраженных в данном языке.

Лингвистическая переменная—это обозначение, допускающее подстановку на свое место лингвистического знака или результата выполнения определенных действий.

Лингвистическая формула—форма записи элементов, среди которых есть хотя бы одна лингвистическая переменная.

Металингвистическая переменная—это обозначение названия правила, требующее на место названия подстановки соответствующей лингвистической формы, лингвистической формулы, либо другой лингвистической переменной.

Металингвистическая форма— заданная форма записи лингвистических форм, формул и металингвистических переменных.

Металингвистическая формула—это металингвистическая форма, в которой есть название в виде металингвистической формы и набора инструкций в виде металингвистических форм.

Формальные грамматики – это средства описания формального языка.

Формальная грамматика — способ описания формального языка, то есть выделения некоторого подмножества из множества всех слов некоторого конечного алфавита. Различают порождающие и распознающие (или аналитические) грамматики — первые задают правила, с помощью которых можно построить любое слово языка, а вторые позволяют по данному слову определить, входит оно в язык или нет.

Формальный синтаксис языка и грамматика языка— это совокупность металингвистических форм.

Билет 2.

Система счисления – это соглашение о представлении чисел посредством конечной совокупности символов (цифр), называемой алфавитом. Каждой цифре ставится в соответствие определенный количественный эквивалент.

Системы счисления разделяют на позиционные и непозиционные.

Непозиционная система счисления – это система, в которой цифры не меняют своего количественного эквивалента в зависимости от местоположения (позиции) в записи числа (система римских цифр).

Позиционная система счисления – смысл информации зависит от позиции пунктуационных знаков (десятичная система счисления).

Правила перевода числа в другую, не десятичную систему счисления различаются для целых и дробных чисел.

Перевод целого числа X осуществляется по следующему алгоритму:

1) получить цифру числа n-ой системы счисления как остаток от деления числа X на основание новой системы счисления n; полученную цифру приписать слева от имеющихся цифр;

2) принять за X частное от деления числа X на основание системы счисления n;

3) выполнять шаги 1-2, пока X  0.

Перевод из шестнадцатеричной в двоичную систему счисления - каждая цифра шестнадцатеричного числа заменяется тетрадой (четырьмя битами), являющейся представлением этой цифры в двоичной системе счисления (тоже самое с восьмеричной системой счисления только там берутся триады).

Перевод из двоичной в шестнадцатеричную систему счисления - двоичное число делится на тетрады справа налево. Каждая тетрада заменяется соответствующей ей цифрой. Если самая левая тетрада неполная, то есть содержит меньше четырех цифр, то слева от числа дописываются нули (то же самое с восьмеричной системой, только там триады).

Перевод дробных чисел с нулевой целой частью из десятичной в n-ую систему счисления - дробное число X, у которого целая часть равна 0, переводится из десятичной в n-ую систему счисления по следующему алгоритму:

1) умножить X на n;

2) получить цифру как целую часть числа X и приписать ее справа от имеющихся цифр;

3) обнулить целую часть числа X;

4) выполнять шаги 1-3, пока X  0 (при точном переводе) или до получения нужного количества цифр в дробной части (при приближенном переводе с заданной точностью).

Пример. Перевести число 0,6875 в двоичную систему счисления.

Решение. Вновь схему перевода запишем в виде столбца.

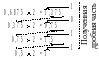
На последнем шаге перевода получена единица. После обнуления целой части получим 0. Значит, перевод закончен. Результат перевода числа 0,6875 в двоичную систему счисления – число 0,1011₂. Перевод из 2-ичной в 10-ичную систему осуществляется «поразрядной суммой» (то есть если переводить число 101,101 из двоичной в десятичную, мы получаем:

2^2*1+2^1*0+2^0*1+2^-1*1+2^-2*0+2^-3*=4*1+2*0+1*1+0,5*1+0,25*1+0,125*1= =4+1+0,5+0,125=5,625. )

Обратный код.

Дополнительный код— наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа и прибавлением к инверсии единицы , либо вычитанием числа из нуля.

Прямой код-- код, полученный заменой старшего бита на 1 в отрицательных числах (у положительных чисел прямой код совпадает с исходным).

Обратный код— код, полученный побитовой инверсией (инверсия нулей и единиц).

Дополнительный код—«обратный код, к которому прибавили единицу» (но Деон скорее всего затребует то длинное определение которое сверху).

Нормализация вещественных чисел.

Нормализованная запись отличного от нуля действительного числа - это запись вида а = ±m×Рq (например 105=1,05*10^2),где q - целое число (положительное, отрицательное или ноль), а m - правильная Р-ичная дробь (грубо говоря Р—это основание системы счисления в которой записано число ), у которой первая цифра после запятой не равна нулю, т.е. 1/Р ≤ m < 1. При этом m называется мантиссой числа, q - порядком числа. Первая (левая) цифра мантиссы нормализованного числа отлична от 0 (за исключением числа ноль), в двоичной системе счисления она всегда равна 1. Билет 3.(литерал) Литерал— запись в исходном коде компьютерной программы, представляющая собой фиксированное значение. Литералы представляют собой константы, непосредственно включаемые в текст программы в отличие от прочих данных — констант и переменных, обращение к которым осуществляется посредством ссылок. Литералы не могут быть изменены в тексте программы. Литерал— это особая категория слов языка. Для каждого подмножества литералов используются собственные правила словообразования. Литерал: целый-литерал символьный-литерал литерал-с-плавающей-точкой строковый-литерал логический-литерал цифровая-последовательность Целый-литерал: десятичный-литерал целый-суффикс (opt) восьмеричный-литерал целый-суффикс (opt)

шестнадцатиричный-литерал целый-суффикс (opt)

литерал-с-плавающей-точкой:

дробная-константа показатель_opt плавающий-суффикс_opt

цифровая-последовательность показатель плавающий-суффикс_opt

дробная-константа:

цифровая-последовательность_opt. цифровая-последовательность

цифровая-последовательность.

показатель:

e знак_opt цифровая-последовательность

E знак_opt цифровая-последовательность

цифровая последовательность:

цифра -

цифровая-последовательность цифра

плавающий-суффикс: одно из

f l F L

логический-литерал:

false

true

Билет 4. (идентификатор)

Формальное определение идентификатора имеет следующий вид:

идентификатор:

не-цифра

идентификатор не-цифра

идентификатор цифра

не-цифра: одно из

a b c d e f g h i j k l m n o p q r s t u v w x y z _

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

цифра: одно из

0 1 2 3 4 5 6 7 8 9

Билет 5.(единица-трансляции)

единица-трансляции:

последовательность-объявлений

последовательность-объявлений:

объявление

последовательность-объявлений объявление

объявление:

объявление-блока

определение-функции

определение-функции:

последовательность-спецификаторов-объявлений

объявитель тело-функции

Тело-функции:

составная-инструкция

Инструкция:

составная-инструкция {}

инструкция-объявление int n

инструкция-выражение a+b

инструкция-выбора if

инструкция-итерации while, for, do while, foreach

инструкция-перехода returt, break, goto, continue

помеченная-инструкция y:a=b+c

Составная-инструкция:

{последовательность-инструкций_opt}

Последовательность-инструкций:

Инструкция

Последовательность-инструкций инструкция

Инструкция-объявление:

объявление-блока

Инструкция-выражение:

выражение

Билет 6. (простое объявление)

простое-объявление:

последовательность-спецификаторов-объявлений_opt

список-инициализирующих-объявлений_opt;

спецификатор-объявления:

спецификатор-типа

typedef

последовательность-спецификаторов-объявлений:

последовательность-спецификаторов-объявлений_opt

спецификатор-объявления

имя-typedef:

идентификатор

спецификатор-типа:

спецификатор-простого-типа

спецификатор-класса

спецификатор-простого-типа:

char

wchar_t

bool

short

int

long

signed

unsigned

float

double

void

имя-типа:

имя-класса

имя-перечисления

имя-typedef

Спецификатор-класса:

заголовок-класса {спецификация-членов_opt}

Заголовок-класса:

ключевое-слово-класса. идентификатор_opt

Ключевое-слово-класса:

union

klass

struct

Список-инициализирующих- объявителей:

инициализирующий-объявитель

список- инициализирующих объявителей, иниц.-объявитель

Инициализирующий-объявитель:

объявитель инициализатор

Объявитель:

идентификатор

объявитель (конструкция-объявления-параметров)

объявитель [выражение_опт] //выражение массива или указатель массива

Инициализатор:

=конструкция-инициализатора

Конструкция-инициализатора:

выражение-присваивания

Билет 7. (формализация инструкции)

инструкция:

помеченная-инструкция

инструкция-выражение

составная-инструкция

инструкция-выбора

инструкция-итерации

инструкция-перехода

инструкция-объявления

блок-try

помеченная-инструкция:

идентификатор:инструкция

case константное-выражение:инструкция

default:инструкция

инструкция-выражение:

выражение_opt;

составная-инструкция:

{последовательность-инструкций_opt}

последовательность-инструкций:

инструкция

последовательность-инструкций инструкция

инструкция-выбора:

if(условие)инструкция

if(условие)инструкция else инструкция

switch(условие)инструкция

условие:

выражение

последовательность-спецификаторов-типа объявитель=выражение-присваивания

инструкция-итерации:

while(условие)инструкция

do инструкция while(выражение);

for(инструкция-инициализации-for условие_opt;выражение_opt)инструкция

инструкция-инициализации-for:

инструкция-выражение

простое-объявление

инструкция-перехода:

break;

continue;

return выражение_opt;

goto идентификатор;

инструкция-объявления:

объявления-блока

Теоретической основой структурного программирования принято считать принципы, изложенные в классической работе Бома и Джакопини [4]. Эта работа в оригинале на итальянском языке была опубликована в 1965 г., а в английском переводе - в 1966 г.

В соответствии с так называемой "структурной" теоремой, сформулированной и доказанной в этой работе, всякая программа может быть построена с использованием только трех основных типов блоков [4].

1. Функциональный блок. Ему в языках программирования соответствуют операторы ввода и вывода или любой оператор (группа операторов) присваивания. В виде функционального блока может быть изображена любая последовательность операторов, выполняющихся один за другим, имеющая один вход и один выход.

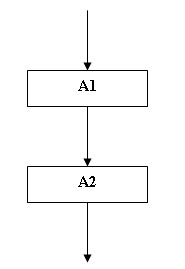Рис.1. Функциональный блок

2. Условная конструкция. Этот блок включает проверку некоторого логического условия (P), в зависимости от которого выполняется либо оператор S1, либо оператор S2: If P Then S1 Else S2;.

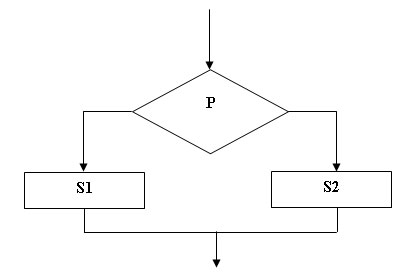Рис.2. Условная конструкция

3. Блок обобщенного цикла. Этот блок обеспечивает многократное повторение выполнения оператора(ов) S, пока выполнено логическое условие P. Аналог блока обобщенного цикла на языке Pascal: While P Do S; .

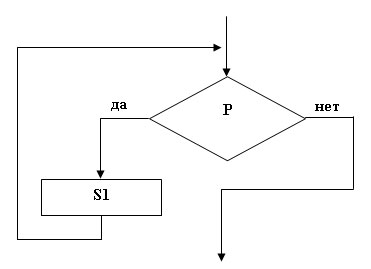Рис.3. Циклическая конструкция

Важной особенностью всех перечисленных блоков является то, что каждый из них имеет один вход и один выход.

Принципы: 1.)Последовательность выполнения блока.

2.)Каждый блок имеет только один вход и только один выход

3.)Безусловный переход goto возможен только внутри блока

Билет 8. (инструкция объявления)

инструкция-объявления:

объявления-блока

объявления-блока:

простое-объявление

простое-объявление:

последовательность-спецификаторов-объявлений_opt

список-инициализирующих-объявлений_opt;

последовательность-спецификаторов-объявлений:

последовательность-спецификаторов-объявлений_opt

спецификатор-объявления

спецификатор-объявления:

спецификатор-типа

typedef

имя-typedef:

идентификатор

спецификатор-типа:

спецификатор-простого-типа

спецификатор-класса

спецификатор-простого-типа:

char

wchar_t

bool

short

int

long

signed

unsigned

float

double

void

Спецификатор-класса:

заголовок-класса {спецификация-членов_opt}

Заголовок-класса:

ключевое-слово-класса. идентификатор_opt

Ключевое-слово-класса:

union

klass

struct

Список-инициализирующих- объявителей:

инициализирующий-объявитель

список- инициализирующих объявителей, иниц.-объявитель

Инициализирующий-объявитель:

объявитель инициализатор

Объявитель:

идентификатор

объявитель (конструкция-объявления-параметров)

объявитель [выражение_опт] //выражение массива или указатель массива

Инициализатор:

=конструкция-инициализатора

Конструкция-инициализатора:

выражение-присваивания

Билеты 9. (инструкция-выражения)

Инструкция-выражение:

выражение_opt

Список-выражений:

выражение-присваивания

Выражение-присваивания:

условное- выражение

выражение-логического-ИЛИ

оператор-присваивания

выражение-присваивания

Оператор-присваивания: одно из

= *= /= %= += -= >>= <<= &= ^= |=

Условное- выражение:

выражение-логического-ИЛИ

выражение-логического-ИЛИ?выражение:выражение-присваивания

Выражение-логического-ИЛИ:

Выражение-логического-И

выражение-логического-ИЛИ || выражение-логического-

Булевы функции.

Конъюнкция — логическая операция, по своему применению максимально приближенная к союзу "и". Синонимы: логическое "И", логическое умножение, иногда просто "И".

В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности.

Дизъюнкция — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу».

В булевой алгебре дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Правило: результат равен , если все операнды равны ; во всех остальных случаях результат равен .

Билеты 10. (битовая конъюнкция)

Выражение-И(битовая конъюнкция):

выражение-равенства

выражение-И&выражение-равенства

Выражение-равенства(эквивалентности):

Выражение-отношения

Выражение-равенства == выражение-отношения

(выражение-равенства != выражение-отношения)

Выражение-отношения: a<b

Выражение-сдвига a<c<<d(сначала сдвиг)

Выражение-отношения < выражение-сдвига

<=

>

>=

Выражение-сдвига:

Аддитивное-выражение

Выражение-сдвига<<аддитивное-выражение

>>

Билет 11.

Аддитивное-выражение: а + b*c(сначала * выполняется)

Мультипликативное-выражение

Аддитивное-выражение + мультипликативное выражение

-

Мультипликативное-выражение:

Выражение-приведение

Мультипликативное-выражение*выражение-приведение

/

%

Выражение-приведение:

Унарное-выражение

Выражение-приведения

Унарное-выражение

Постсуффиксное-выражение a[i], [ i ] – постсуффиксное выражение

++выражение-приведения

- -

Унарный-оператор выражение-приведения

Унарный-оператор: (участвует только один, например +a, +1, -a, -1)

+ - * & ! ~

Постсуффиксноефи-выражение:

Первичное выражение

Постсуффиксное-выражение:[выражение]

Постфиксное-выражение(список выражений opt) BinaryInt(“b=”,b)

Список-выражений:

Выражение

Список-выражений , выражение

Первичное-выражие:

Литерал

Идентификатор

Билет 12.

инструкция-выбора:

if(условие)инструкция

if(условие)инструкция else инструкция

switch(условие)инструкция

условие:

выражение

последовательность-спецификаторов-типа объявитель=выражение-присваивания

Билет 13.

инструкция-итерации:

while(условие)инструкция

do инструкция while(выражение);

for(инструкция-инициализации-for условие_opt;выражение_opt)инструкция

инструкция-инициализации-for:

инструкция-выражение

простое-объявлени