42. Доказательство теоремы о признаке (достаточном условии) существования седловой точки матрицы игры размерности 2х2.

Для того чтобы у матрицы А размером 2x2 существовала седловая точка, достаточно, чтобы сумма элементов главной диагонали матрицы А равнялась сумме элементов ее побочной диагонали:

a₁₁+a₂₂ = a₁₂+a₂₁ (1)

Доказательство. Из равенства (1)

a₂₁ = a₁₁ - a₁₂ + a₂₂ (2)

Возможныслучаи:

a₁₁<a₁₂ (3)

или

a₁₁>a₁₂ (4)

В случае (3) из (2) получаем неравенство а₂₁< а₂₂, которое вместе с неравенством (3) означает, что второй столбец матрицы А доминируется ее первым столбцом. Тогда на основании предложения 2 следствия 11.1( Если l-й столбец матрицы игры доминируется (строго доминируется) некоторым другим столбцом, то существует (любая) оптимальная смешанная стратегия игрока В, в которую чистая стратегия В₁ входит с нулевой вероятностью) существует оптимальная смешанная стратегия игрока В, в которую чистая стратегия В₂ входит с нулевой вероятностью (другими словами, в данном случае стратегия В₁ является оптимальной). Следовательно, стратегия В₂ пассивна, и потому в силу теоремы 14.2(вопрос 41) у матрицы А существует седловая точка.

Если же имеет место случай (4), то из (2) вытекает неравенство а₂₁> а₂₂, которое вместе с (4) означает строгую доминируемость первого столбца матрицы А ее вторым столбцом. А потому на основании того же предложения 2 следствия 11.1(Если l-й столбец матрицы игры доминируется (строго доминируется) некоторым другим столбцом, то существует (любая) оптимальная смешанная стратегия игрока В, в которую чистая стратегия В₁ входит с нулевой вероятностью) стратегия В₁ является пассивной и, следовательно, по теореме 14.2 (вопрос 41) у матрицы А существует седловая точка.

43. Вывод формул для нахождения оптимальных смешанных стратегий игрока а и цены игры размерности 2х2 без седловой точки.

Так как матрица А не имеет седловой точки, то нижняя цена игры в чистых стратегиях а меньше верх­ней цены игры в чистых стратегиях Поэтому решения игры в чистых стратегиях не существует и надо искать решение игры в смешанных стратегиях.

В этом случае в соответствии со следствием выполняется условие

.

Пусть — оптимальная смешанная стратегия игрока A (которая всегда существует по основной теореме матричных игр фон Неймана) и V – цена игры.

Так как матрица А не имеет седловых точек, то пассивных стратегий в игре не существует. Поэтому стратегии В₁ и В₂ активны. Тогда Записывая ле­вые части этих равенств по формуле и присоединяя к ним нормировочное условие получим систему трех ли­нейных алгебраических уравнений

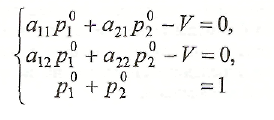
с тремя неизвестными Определитель этой системы

в силу выполнимости условия . Поэтому система имеет единственное решение, которое можно найти по формулам Крамера. Для этого вычислим определители

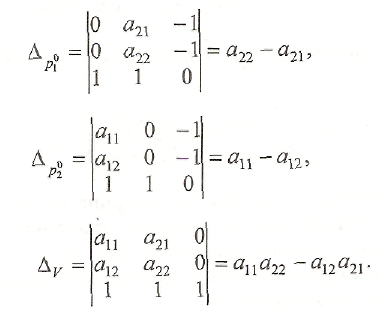
Тогда по формулам Крамера

получаем требуемые формулы

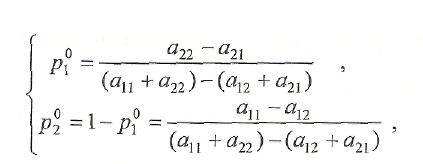и