- •Вопрос 1
- •Вопрос 2
- •1) Понятие слау
- •2) Правило Крамера решения слау
- •3) Метод Гаусса
- •4) Ранг матрицы, теорема Кронекера-Капелли
- •I Понятие ранга матрицы
- •II Вычисление ранга матрицы
- •I II Теорема Кронекера-Капелли
- •5) Решение слау обращением матрицб понятие обусловленности матриц
- •I Решение слау обращением матриц
- •II Вычисление обратной матрицы путём решения системы линейных уравнений
- •III Понятие обусловленности матриц
- •Вопрос 4
- •Вопрос 5 Скалярное произведение векторов
- •Длина вектора
- •Угол между векторами
- •Вопрос 6
- •Вопрос 7 Вопрос 8
- •Эллипс как кривая второго порядка
- •[Править]Канонический вид
- •Вопрос 9
- •Вопрос 10
- •Вопрос 11
- •Вопрос 13
- •2. Свойства сохранения порядка
- •Вопрос 14
- •14 Вопрос.
- •Вопрос 15 Производная.
- •Производная постоянной.
- •Производная степенной функции.
- •Производная показательной функции.
- •Производная логарифмической функции.
- •Производные тригонометрических функций.
- •Производные обратных тригонометрических функций.
- •Производные гиперболических функций.
- •Физический смысл.
- •Вопрос 16
- •Вопрос 18
- •Вопрос 19 Выпуклость функции. Направление выпуклости. Точки перегиба. Условия выпуклости и перегиба.
Вопрос 18
18. Интервалы монотонности функции. Локальные экстремумы.
Монотонная функция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное.
Интервалом монотонности функции можно назвать промежуток, в котором функция либо только возрастает, либо только убывает.
Достаточные признаки монотонности функции.
Если f '( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.
Если f '( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.
Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.
Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.
Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум).
Экстремум — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Необходимое условие экстремума. Если x0 - точка экстремума функции f ( x ) и производная f’ существует в этой точке, то f’ ( x0 ) = 0.Эта теорема - необходимое условие экстремума
Функция у = f(х) имеет максимум (минимум) в точке x0, если существует такая окрестность точки x0, что для всех x, принадлежащих этой окрестности, выполняется условие f(х) < f(х0) (f (х) > f(х0), х¹ х0.
Достаточное условие локального экстремума.
Пусть функция у = f(х) дифференцированна в некоторой точке, тогда если производная функции у = f(х) при прохождение через точку х0 сменяет знак с + на -, точка точка х0 является локальным максимумом.
Если сменяет знак с – на +, точка x0 явлется локальным минимумом.
Вопрос 19 Выпуклость функции. Направление выпуклости. Точки перегиба. Условия выпуклости и перегиба.
При исследовании функции и построении ее графика на одном из этапов мы определяем точки перегиба и интервалы выпуклости. Эти данные вместе с промежутками возрастания и убывания позволяют схематично представить график исследуемой функции. Дальнейшее изложение подразумевает, что Вы умеете находить производные функции до некоторого порядка и решать различные виды неравенств. Изучение материала начнем с необходимых определений и понятий. Далее озвучим связь между значением второй производной функции на некотором интервале и направлением ее выпуклости. После этого перейдем к условиям, которые позводляют определять точки перегиба графика функции. По тексту будем приводить характерные примеры с подробными решениями.
Определения и понятия.
Нахождение интервалов выпуклости функции.
Необходимое и достаточные условия перегиба.
Определения и понятия.
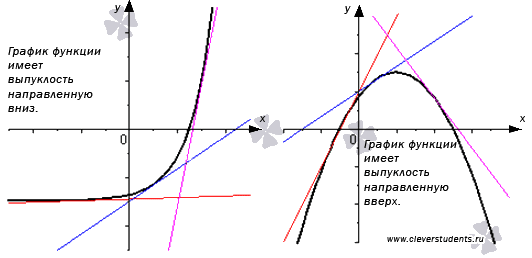
Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервалаХ. Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервалаХ.
Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой. Посмотрите на чертеж, иллюстрирующий эти определения.
Точка ![]() называется точкой
перегиба графика функции y
= f(x),
если в данной точке существует касательная
к графику функции (она может быть
параллельна оси Оу)
и существует такая окрестность точки
называется точкой
перегиба графика функции y
= f(x),
если в данной точке существует касательная
к графику функции (она может быть
параллельна оси Оу)
и существует такая окрестность точки ![]() ,
в пределах которой слева и справа от
точки М график
функции имеет разные направления
выпуклости.
Другими словами,
точка М называется
точкой перегиба графика функции, если
в этой точке существует касательная и
график функции меняет направление
выпуклости, проходя через нее.
Если
необходимо, обратитесь к разделу касательная
к графику функции в точке,
чтобы вспомнить условия существования
невертикальной и вертикальной
касательной.
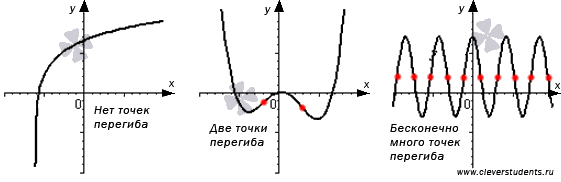
На рисунке ниже
представлены несколько примеров точек
перегиба (отмечены красными точками).
Заметим, что некоторые функции могут
не иметь точек перегиба, а другие могут
иметь одну, несколько или бесконечно
много точек перегиба.
,
в пределах которой слева и справа от
точки М график
функции имеет разные направления
выпуклости.
Другими словами,
точка М называется
точкой перегиба графика функции, если
в этой точке существует касательная и
график функции меняет направление
выпуклости, проходя через нее.
Если
необходимо, обратитесь к разделу касательная
к графику функции в точке,
чтобы вспомнить условия существования
невертикальной и вертикальной
касательной.
На рисунке ниже
представлены несколько примеров точек
перегиба (отмечены красными точками).
Заметим, что некоторые функции могут
не иметь точек перегиба, а другие могут
иметь одну, несколько или бесконечно
много точек перегиба.
Нахождение интервалов выпуклости функции.
Сформулируем
теорему, которая позволяет определять
промежутки выпуклости функции.
Если
функция y
= f(x) имеет
конечную вторую производную на
интервале Х и
если выполняется неравенство ![]() (
(![]() ),
то график функции имеет выпуклость
направленную вниз (вверх) на Х.
Эта
теорема позволяет находить промежутки
вогнутости и выпуклости функции, нужно
лишь на области определения исходной
функции решить
неравенства
),
то график функции имеет выпуклость
направленную вниз (вверх) на Х.
Эта
теорема позволяет находить промежутки
вогнутости и выпуклости функции, нужно
лишь на области определения исходной
функции решить
неравенства ![]() и
и ![]() соответственно.
Следует
отметить, что точки, в которых функция y
= f(x) определена,
а вторая производная не существует,
будем включать в интервалы вогнутости
и выпуклости.
Разберемся с этим
на примере.
Пример.
Выяснить
промежутки, на которых график
функции
соответственно.
Следует
отметить, что точки, в которых функция y
= f(x) определена,
а вторая производная не существует,
будем включать в интервалы вогнутости
и выпуклости.
Разберемся с этим
на примере.
Пример.
Выяснить
промежутки, на которых график
функции  имеет
выпуклость направленную вверх и
выпуклость направленную
вниз.
Решение.
Областью
определения этой функции является все
множество действительных чисел. Найдем
вторую производную.
имеет
выпуклость направленную вверх и
выпуклость направленную
вниз.
Решение.
Областью
определения этой функции является все
множество действительных чисел. Найдем
вторую производную.
 Область
определения второй производной совпадает
с областью определения исходной функции,
поэтому, чтобы выяснить интервалы
вогнутости и выпуклости, достаточно
решить
и
соответственно.
Область
определения второй производной совпадает
с областью определения исходной функции,
поэтому, чтобы выяснить интервалы
вогнутости и выпуклости, достаточно
решить
и
соответственно.
 Следовательно,
функция выпуклая вниз на интервале
Следовательно,
функция выпуклая вниз на интервале ![]() и
выпуклая вверх на интервале
и
выпуклая вверх на интервале ![]() .
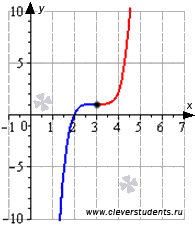
Графическая
иллюстрация.
Часть
графика функции на интервале выпуклости
изображена синим цветом, на интервале
вогнутости – красным цветом.
.
Графическая
иллюстрация.
Часть
графика функции на интервале выпуклости
изображена синим цветом, на интервале
вогнутости – красным цветом.

Сейчас
рассмотрим пример, когда область
определения второй производной не
совпадает с областью определения
функции. В этом случае, как мы уже
отмечали, точки области определения, в
которых не существует конечная вторая
производная, следует включать в интервалы
выпуклости и (или) вогнутости.
Пример.
Найти
промежутки выпуклости и вогнутости
графика функции 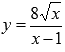 .
Решение.
Начнем
с области определения функции:
.
Решение.
Начнем
с области определения функции:
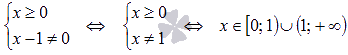 Найдем
вторую производную:
Найдем
вторую производную:
 Областью
определения второй производной является
множество
Областью
определения второй производной является
множество ![]() .
Как видите, x
= 0 принадлежит
области определения исходной функции,
но не принадлежит области определения
второй производной. Не забывайте про
эту точку, ее нужно будет включить в
интервал выпуклости и (или) вогнутости.
Теперь
решаем неравенства
и
на
области определения исходной функции.
Воспользуемся обобщенным
методом интервалов.
Числитель выражения
.
Как видите, x
= 0 принадлежит
области определения исходной функции,
но не принадлежит области определения
второй производной. Не забывайте про
эту точку, ее нужно будет включить в
интервал выпуклости и (или) вогнутости.
Теперь
решаем неравенства
и
на
области определения исходной функции.
Воспользуемся обобщенным
методом интервалов.
Числитель выражения 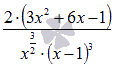 обращается
в ноль при
обращается
в ноль при 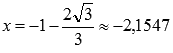 или
или ![]() ,
знаменатель – при x
= 0 или x
= 1.
Схематично наносим эти точки на числовую
прямую и выясняем знак выражения на
каждом из интервалов, входящих в область
определения исходной функции (она
показана заштрихованной областью на
нижней числовой прямой). При положительном
значении ставим знак «плюс», при
отрицательном – знак «минус».
,
знаменатель – при x
= 0 или x
= 1.
Схематично наносим эти точки на числовую
прямую и выясняем знак выражения на
каждом из интервалов, входящих в область
определения исходной функции (она
показана заштрихованной областью на
нижней числовой прямой). При положительном
значении ставим знак «плюс», при
отрицательном – знак «минус».
 Таким
образом,
Таким
образом,

 Следовательно,
включив точку x
= 0,
получаем ответ.
При
Следовательно,
включив точку x
= 0,
получаем ответ.
При  график
функции имеет выпуклость направленную
вниз, при
график
функции имеет выпуклость направленную
вниз, при 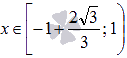 -
выпуклость направленную вверх.
Графическая
иллюстрация.
Часть
графика функции на интервале выпуклости
изображена синим цветом, на интервалах
вогнутости – красным цветом, черной
пунктирной прямой является вертикальная
асимптота.
-
выпуклость направленную вверх.
Графическая
иллюстрация.
Часть
графика функции на интервале выпуклости
изображена синим цветом, на интервалах
вогнутости – красным цветом, черной
пунктирной прямой является вертикальная
асимптота.
Необходимое и достаточные условия перегиба.
Сформулируем необходимое
условие перегиба графика
функции.
Пусть график функции y
= f(x) имеет
перегиб в точке
и
имеет при ![]() непрерывную
вторую производную, тогда выполняется
равенство
непрерывную
вторую производную, тогда выполняется
равенство ![]() .
Из
этого условия следует, что абсциссы
точек перегиба следует искать среди
тех, в которых вторая производная функции
обращается в ноль. НО, это условие не
является достаточным, то есть не все
значения
,
в которых вторая производная равна
нулю,
.
Из
этого условия следует, что абсциссы
точек перегиба следует искать среди
тех, в которых вторая производная функции
обращается в ноль. НО, это условие не
является достаточным, то есть не все
значения
,
в которых вторая производная равна
нулю,
являются
абсциссами точек перегиба.
Еще
следует обратить внимание, что по
определению точки перегиба требуется
существование касательной прямой, можно
и вертикальной. Что это означает? А
означает это следующее: абсциссами
точек перегиба могут быть все
из
области определения функции, для
которых ![]() и
и ![]() .
Обычно это точки, в которых знаменатель
первой производной обращается в
ноль.
После того как найдены
все
,
которые могут быть абсциссами точек
перегиба, следует воспользоваться первым
достаточным условием перегибаграфика
функции.
Пусть функция y
= f(x) непрерывна
в точке
,
имеет в ней касательную (можно вертикальную)
и эта функция имеет вторую производную
в некоторой окрестности точки
.
Тогда, если в пределах этой окрестности
слева и справа от
,
вторая производная имеет разные знаки,
то
является
точкой перегиба графика функции.
Как
видите первое достаточное условие не
требует существования второй производной
в самой точке
,
но требует ее существование в окрестности
точки
.
Сейчас
обобщим всю информацию в виде
алгоритма.
Алгоритм
нахождения точек перегиба функции.
Находим
все абсциссы
возможных
точек перегиба графика функции
(
или
и
)
и выясняем, проходя через какие
вторая
производная меняет знак. Такие значения
и будут абсциссами точек перегиба, а
соответствующие им точки
будут
точками перегиба графика функции.
Рассмотрим
два примера для разъяснения.
Пример.
Найти
точки перегиба и интервалы выпуклости
и вогнутости графика функции
.
Обычно это точки, в которых знаменатель
первой производной обращается в
ноль.
После того как найдены
все
,
которые могут быть абсциссами точек
перегиба, следует воспользоваться первым
достаточным условием перегибаграфика
функции.
Пусть функция y
= f(x) непрерывна
в точке
,
имеет в ней касательную (можно вертикальную)
и эта функция имеет вторую производную
в некоторой окрестности точки
.
Тогда, если в пределах этой окрестности
слева и справа от
,
вторая производная имеет разные знаки,
то
является
точкой перегиба графика функции.
Как
видите первое достаточное условие не
требует существования второй производной
в самой точке
,
но требует ее существование в окрестности
точки
.
Сейчас
обобщим всю информацию в виде
алгоритма.
Алгоритм
нахождения точек перегиба функции.
Находим
все абсциссы
возможных
точек перегиба графика функции
(
или
и
)
и выясняем, проходя через какие
вторая
производная меняет знак. Такие значения
и будут абсциссами точек перегиба, а
соответствующие им точки
будут
точками перегиба графика функции.
Рассмотрим
два примера для разъяснения.
Пример.
Найти
точки перегиба и интервалы выпуклости
и вогнутости графика функции  .
Решение.
Областью
определения функции является все
множество действительных чисел.
.
Решение.
Областью
определения функции является все
множество действительных чисел.
Найдем
первую производную:
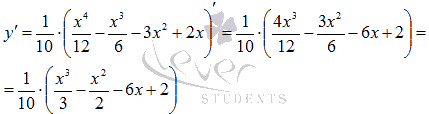 Областью
определения первой производной также
является все множество действительных
чисел, поэтому равенства
и
не
выполняется ни для каких
.
Найдем
вторую производную:
Областью
определения первой производной также
является все множество действительных
чисел, поэтому равенства
и
не
выполняется ни для каких
.
Найдем
вторую производную:
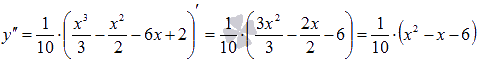 Выясним
при каких значениях аргумента x вторая
производная обращается в ноль:
Выясним
при каких значениях аргумента x вторая
производная обращается в ноль:
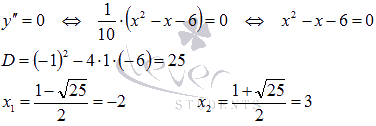 Таким
образом, абсциссами возможных точек
перегиба являются x
= -2 и x
= 3.
Теперь
осталось проверить по достаточному
признаку перегиба, в каких из этих точек
вторая производная меняет знак. Для
этого нанесем точки x
= -2 и x
= 3 на
числовую ось и, как в обобщенном
методе интервалов,
расставим знаки второй производной над
каждым промежутком. Под каждым интервалом
схематично дугами показано направление
выпуклости графика функции.
Таким
образом, абсциссами возможных точек
перегиба являются x
= -2 и x
= 3.
Теперь
осталось проверить по достаточному
признаку перегиба, в каких из этих точек
вторая производная меняет знак. Для
этого нанесем точки x
= -2 и x
= 3 на
числовую ось и, как в обобщенном
методе интервалов,
расставим знаки второй производной над
каждым промежутком. Под каждым интервалом
схематично дугами показано направление
выпуклости графика функции.
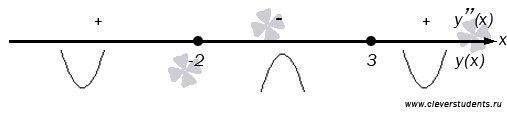 Вторая
производная меняет знак с плюса на
минус, проходя через точку x
= -2 слева
направо, и меняет знак с минуса на плюс,
проходя через x
= 3.
Следовательно, и x
= -2 и x
= 3 являются
абсциссами точек перегиба графика
функции. Им соответствуют точки
графика
Вторая
производная меняет знак с плюса на
минус, проходя через точку x
= -2 слева
направо, и меняет знак с минуса на плюс,
проходя через x
= 3.
Следовательно, и x
= -2 и x
= 3 являются
абсциссами точек перегиба графика
функции. Им соответствуют точки
графика ![]() и
и ![]() .
Взглянув
еще раз на числовую ось и знаки второй
производной на ее промежутках, можно
делать вывод об интервалах выпуклости
и вогнутости. График функции
.
Взглянув
еще раз на числовую ось и знаки второй
производной на ее промежутках, можно
делать вывод об интервалах выпуклости
и вогнутости. График функции
выпуклый
на интервале ![]() и
вогнутый на интервалах
и
вогнутый на интервалах ![]() и
и ![]() .
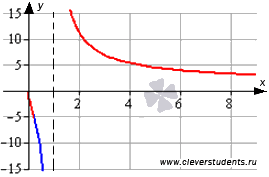
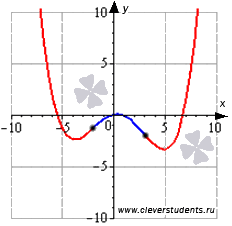
Графическая
иллюстрация.
Часть
графика функции на интервале выпуклости
изображена синим цветом, на интервалах
вогнутости – красным цветом, точки
перегиба показаны черными точками.
.
Графическая
иллюстрация.
Часть
графика функции на интервале выпуклости
изображена синим цветом, на интервалах
вогнутости – красным цветом, точки
перегиба показаны черными точками.
Пример.
Найдите
абсциссы всех точек перегиба графика
функции 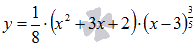 .
Решение.
Областью
определения данной функции является
все множество действительных чисел.
Найдем
производную.
.
Решение.
Областью
определения данной функции является
все множество действительных чисел.
Найдем
производную.
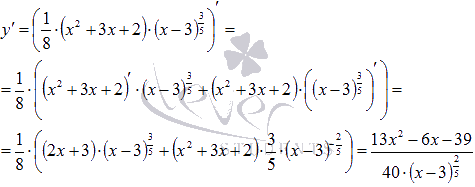 Первая
производная, в отличии от исходной
функции, не определена при x
= 3.
Но
Первая
производная, в отличии от исходной
функции, не определена при x
= 3.
Но  и
и  .
Следовательно, в точке с абсциссой x
= 3 существует
вертикальная касательная к графику
исходной функции. Таким
.
Следовательно, в точке с абсциссой x
= 3 существует
вертикальная касательная к графику
исходной функции. Таким
образом, x
= 3 может
быть абсциссой точки перегиба графика
функции.
Находим вторую производную,
область ее определения и точки, в которых
она обращается в ноль:
 Получили
еще две возможные абсциссы точек
перегиба. Отмечаем все три точки на
числовой прямой и определяем знак второй
производной на каждом из полученных
интервалов.
Получили
еще две возможные абсциссы точек
перегиба. Отмечаем все три точки на
числовой прямой и определяем знак второй
производной на каждом из полученных
интервалов.
 Вторая
производная меняет знак, проходя через
каждую из точек, следовательно, все они
являются абсциссами точек
перегиба.
Графическая
иллюстрация.
Части
графика функции на интервалах выпуклости
изображены синим цветом, на интервалах
вогнутости – красным цветом, точки
перегиба показаны черными точками.
Вторая
производная меняет знак, проходя через
каждую из точек, следовательно, все они
являются абсциссами точек
перегиба.
Графическая
иллюстрация.
Части
графика функции на интервалах выпуклости
изображены синим цветом, на интервалах
вогнутости – красным цветом, точки
перегиба показаны черными точками.

Первое
достаточное условие перегиба графика
функции позволяет определять точки
перегиба и не требуют существования
второй производной в них. Поэтому, первое
достаточное условие можно считать
универсальным и самым используемым.
Сейчас
сформулируем еще два достаточных условия
перегиба, но они применимы лишь при
существовании конечной производной в
точке перегиба до некоторого
порядка.
Второе
достаточное условие перегиба графика
функции.
Если
,
а ![]() ,
тогда
является
абсциссой точки перегиба графика
функции y
= f(x).
Пример.
Выяснить,
является ли точка
,
тогда
является
абсциссой точки перегиба графика
функции y
= f(x).
Пример.
Выяснить,
является ли точка ![]() точкой
перегиба графика функции
точкой
перегиба графика функции ![]() .
Решение.
Для
начала убедимся, что точка
принадлежит
графику функции:
.
Решение.
Для
начала убедимся, что точка
принадлежит
графику функции:
![]() Функция
определена для всех действительных
значений аргумента. Найдем первую и
вторую производные.
Функция
определена для всех действительных
значений аргумента. Найдем первую и
вторую производные.
 Вторая
производная обращается в ноль при x
= 3,
то есть необходимое условие перегиба
графика функции в точке
выполнено,
и эта точка может быть точкой перегиба.
Воспользуемся вторым достаточным
условием перегиба. Для этого найдем
третью производную и убедимся, что ее
значение при x
= 3отлично
от нуля.
Вторая
производная обращается в ноль при x
= 3,
то есть необходимое условие перегиба
графика функции в точке
выполнено,
и эта точка может быть точкой перегиба.
Воспользуемся вторым достаточным
условием перегиба. Для этого найдем
третью производную и убедимся, что ее
значение при x
= 3отлично
от нуля.
 Очевидно,
что значение третьей производной отлично
от нуля для любых x,
в том числе и для x
= 3.
Поэтому, по второму достаточному условию
перегиба графика функции, точка
является
точкой перегиба.
Графическая
иллюстрация.
Часть
графика функции на интервале выпуклости
изображена синим цветом, на интервале
вогнутости – красным цветом, точка
перегиба показана черной точкой.
Очевидно,
что значение третьей производной отлично
от нуля для любых x,
в том числе и для x
= 3.
Поэтому, по второму достаточному условию
перегиба графика функции, точка
является
точкой перегиба.
Графическая
иллюстрация.
Часть
графика функции на интервале выпуклости
изображена синим цветом, на интервале
вогнутости – красным цветом, точка
перегиба показана черной точкой.

Третье
достаточное условие перегиба графика
функции.
Пусть ![]() ,
а
,
а ![]() ,
тогда если n –
четное число, то
является
абсциссой точки перегиба графика
функцииy
= f(x).
Пример.
,
тогда если n –
четное число, то
является
абсциссой точки перегиба графика
функцииy
= f(x).
Пример.
Найдите
точки перегиба графика
функции ![]() .
Решение.
Функция
определена на всем множестве действительных
чисел.
Найдем ее производную:
.
Решение.
Функция
определена на всем множестве действительных
чисел.
Найдем ее производную: ![]() .
Очевидно, что она также определена для
всех действительных x,
поэтому, в любой из точек ее графика
существует невертикальная
касательная.
Определим значения х,
при которых вторая производная обращается
в ноль.
.
Очевидно, что она также определена для
всех действительных x,
поэтому, в любой из точек ее графика
существует невертикальная
касательная.
Определим значения х,
при которых вторая производная обращается
в ноль.
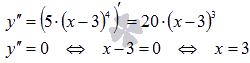 Таким
образом, в точке с абсциссой x
= 3 может
быть перегиб графика функции. Чтобы
убедиться в том, что х
= 3 действительно
абсцисса точки перегиба, воспользуемся
третьим достаточным условием.
Таким
образом, в точке с абсциссой x
= 3 может
быть перегиб графика функции. Чтобы
убедиться в том, что х
= 3 действительно
абсцисса точки перегиба, воспользуемся
третьим достаточным условием.
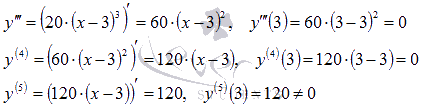 По
третьему достаточному условию перегиба
графика функции имеем n
= 4 (пятая
производная обращается в ноль) – четное,
поэтому x
= 3 является
абсциссой точки перегиба и ей соответствует
точка графика функции (3;
1).
Графическая
иллюстрация.
Часть
графика функции на интервале выпуклости
изображена синим цветом, на интервале
вогнутости – красным цветом, точка
перегиба показана черной точкой.
По
третьему достаточному условию перегиба
графика функции имеем n
= 4 (пятая
производная обращается в ноль) – четное,
поэтому x
= 3 является
абсциссой точки перегиба и ей соответствует
точка графика функции (3;
1).
Графическая
иллюстрация.
Часть
графика функции на интервале выпуклости
изображена синим цветом, на интервале
вогнутости – красным цветом, точка
перегиба показана черной точкой.