5. Основные свойства математического ожидания и дисперсии.

Свойства математического ожидания: 1. M( C )=C, где С – константа, 2. M(CX)=CM(X), 3. M(X+Y)=M(X)+M(Y), 4. , если Х и У – стат. независ. Свойства дисперсии: 1. D(C) = 0, 2. D(X+У)=D(X)+D(Y), 3. D(CX)=C²D(X), 4. D(X*У) =D(X)*D(Y).

6. Основные распределения св (краткий обзор).

1. Распределение вероятностей называется равномерным, если на интервале возможных значений случайной величины плотность распределения является постоянной. Из следует, что плотность равномерного распределения дается формулой

Непрерывная случайная величина x, принимающая значения на отрезке [a, b], распределена равномерно на [a, b], если плотность распределения px(x) и функция распределения Fx(x) случайной величины x имеют соответственно вид: Числовые характеристики: .

2. Биноминальное распределение. Дискретная случайная величина Х имеет биноминальный закон распределение, если она принимает значения 0, 1, 2, …m… n с вероятностями , 0< p <1, q = 1 – p, m = 0, 1, 2, …n. Как видно, вероятность значений находится по формуле Бернулли. Следовательно, биноминальный закон распределения представляет собой распределение числа Х = m, количества событий А, произошедших в n испытаниях. Бернулли, в каждом из которых событие A происходит с вероятностью p, а противоположное событие с вероятностью 1- p.. Закон распределения биноминальной случайной величины Х в развёрнутом форме имеет вид: - верхняя строчка - это совокупность числовых значений, которые может принимать случайная величина; - нижняя строчка - вероятность события, что случайная величина примет эти значения. Определение биноминального закона корректно, так как основное свойство ряда распределения выполнено, ибо , как было отмечено выше, есть сумма всех членов разложения бинома Ньютона: . Отсюда и название закона – биноминальный. Числовые характеристики биноминального распределения: 1. М(Х) = np. 2. D(X) = npq. 3. Закон распределения Пуассона. Дискретная случайная величина Х имеет закон распределение Пуассона, если она принимает значения 0, 1, 2, …m,… (бесконечное, но счётное множество значений) с вероятностями , где m = 0, 1, 2, …Числовые характеристики распределения Пуассона: 1. М(Х) = λ. 2. D(X) = λ.

Равномерное распределение вероятностей является простейшим и может быть как дискретным, так и непрерывным. Дискретное равномерное распределение – это такое распределение, для которого вероятность каждого из значений СВ одна и та же, то есть: , где N – количество возможных значений СВ. Распределение вероятностей непрерывной CВ Х, принимающие все свои значения из отрезка [а;b] называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю: . 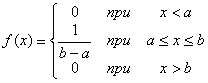Среднее значение и дисперсия этого распределения равны соответственно

 ,  .

7. Биноминальное распределение св. Числовые характеристики биноминального распределения. Функция распределения биноминального распределения.

Дискретная случайная величина Х имеет биноминальный закон распределение, если она принимает значения 0, 1, 2, …m… n с вероятностями , 0< p <1, q = 1 – p, m = 0, 1, 2, …n. Как видно, вероятность значений находится по формуле Бернулли. Следовательно, биноминальный закон распределения представляет собой распределение числа Х = m, количества событий А, произошедших в n испытаниях. Бернулли, в каждом из которых событие A происходит с вероятностью p, а противоположное событие с вероятностью 1- p.. Закон распределения биноминальной случайной величины Х в развёрнутом форме имеет вид: - верхняя строчка - это совокупность числовых значений, которые может принимать случайная величина; - нижняя строчка - вероятность события, что случайная величина примет эти значения. Определение биноминального закона корректно, так как основное свойство ряда распределения выполнено, ибо , как было отмечено выше, есть сумма всех членов разложения бинома Ньютона: . Отсюда и название закона – биноминальный. Числовые характеристики биноминального распределения: 1. М(Х) = np. 2. D(X) = npq.