6Способы выражения величины давления.

Из определения давления: Величина давления – нормальное сжимающее напряжение. Измеряется в ед. напряжения (сила/площадь).

 

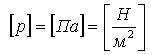
Величину давления можно также представить как высоту столба жидкости h (призматического), вес которого создаёт на нижней его грани напряжение р, равное величине давления .

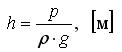                                                                                                          (4.8)

 

Рассмотрим сосуд, заполненный жидкостью, на поверхности жидкости действует давление р₀ (рис 4.4).

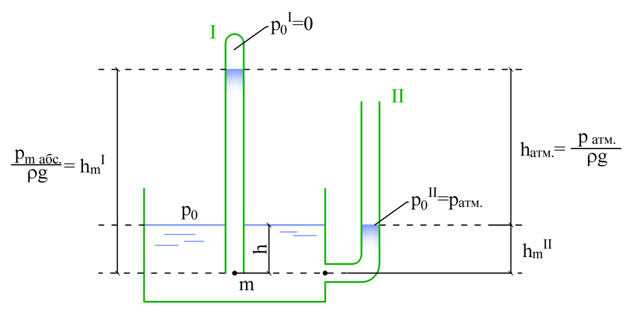
Рис.4.4 Способы выражения величины давления

 

Поместим в этот сосуд стеклянную трубку I, верхний конец которой запаян и из него полностью откачан воздух, т.е. абсолютное давление равно 0. Тогда на поверхность жидкости в этой трубке действует давление р₀^I=0.

Жидкость в такой трубке поднимется на высоту h_m^I относительно основания трубки – точки (.)m. Жидкость в трубке I поднимается до тех пор, пока давление жидкости со стороны сосуда не будет уравновешено давлением жидкости в трубке I.

Давление со стороны сосуда:

                                                                                                (4.9)

 

Давление со стороны трубки I:

,                                                                                          (4.10)

 

где р_m – величина абсолютного давления в точке (.)m.

Таким образом, из уравнения 4.10 можно выразить высоту столба жидкости (h_m^II), который компенсирует величину абсолютного давления p_m.

.

 

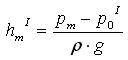Поскольку абсолютное давление на поверхности жидкости в трубке I p_o^I=0 величина h_m характеризует величину абсолютного давления в (.)m (со стороны жидкости в баке).

 

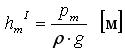
Аналогично для трубки II, верхний конец которой открыт в атмосферу и абсолютное давление на свободной поверхности жидкости в ней p₀^II=p_атм.

,

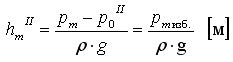т.к. 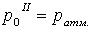 то 

 

            Таким образом, величина h_m^II – высота столба на которую поднимется жидкость под действием избыточного давления

Абсолютное и избыточное давление может быть представлено в виде высоты столба жидкости, на которую она поднимется под действием соответствующего давления.

 

Так величина абсолютного атмосферного давления:

,

 

 

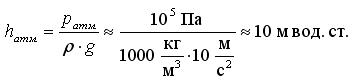
(водного столба, т.к. используется плотность воды)

➨эту же величину можно представить в высоте столба любой жидкости.

Например, плотность ртути при 20ºС – 13546  .

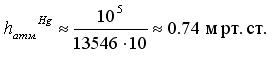
7 Вывод формулы для определения величины силы давления на плоскую стенку.

 

Рассмотрим сосуд, заполненный покоящейся жидкостью. Одна из плоских стенок сосуда имеет наклон под углом α к горизонту. На стенке сосуда наметим плоскую фигуру произвольного очертания площадью ω – показана на проекции (см. рис. 5.1).

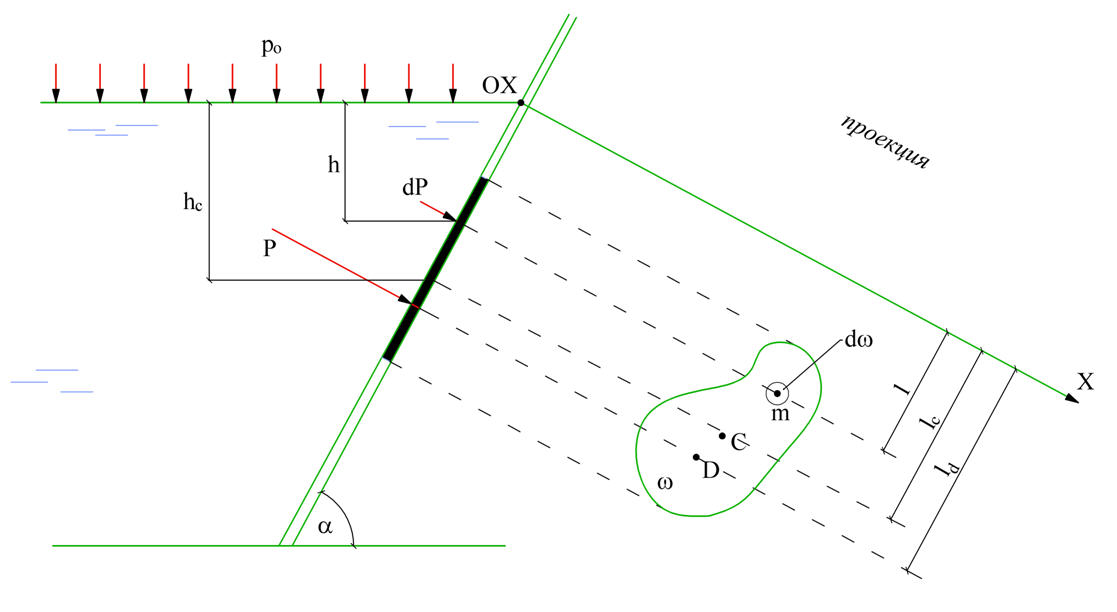
Рис.5.1 К выводу формулы для силы давления на плоскую стенку.

 

В соответствии с I свойством гидростатического давления, давление направлено по нормали к стенке, и т.к. стенка плоская, то в каждой точке фигуры ω давление приложено в одинаковых направлениях (нормально к стенке) ➨ сила гидростатического давления Р, действующая на фигуру ω также направлена по нормали к стенке.

 

Определим величину силы P.

1. Наметим на рассматриваемой фигуре точку m, находящуюся на глубине h под свободной поверхностью жидкости. На проекции рассматриваемой фигуры эта точка имеет координату l, отсчитываемую от оси OX. Соответственно глубина положения точки m и её координата l связаны между собой соотношением:

 

2. Выделим вокруг точки m элементарную площадку dω, в пределах которой можно пренебречь изменением давления (площадка настолько мала, что при перемещении вдоль неё глубина практически не изменяется, а значит и давление не изменяется, т.к. распределено статически (т.е. зависит от глубины)).

Тогда сила давления на площадку dω (часть силы P):

;

где p – давление в точке m.

 

Для определения величины силы P гидростатического давления на фигуру ω, проинтегрируем получившееся выражение для dP по всей площади ω (т.е. сложим части сил приходящиеся на элементарные площадки, из которых состоит фигура ω).

 

 

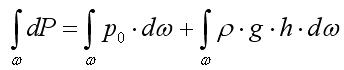
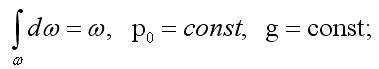
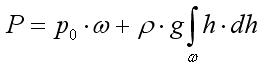
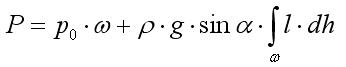
sinα вынесли за знак интеграла, т.к. площадка плоская и угол α не изменяется в пределах всей площади ω.

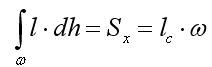 - статический момент плоской фигуры относительно оси OX.

 

l_c – координата центра тяжести сечения от оси OX (см. рис. 5.1).

(S_x – величина, известная из теории сопротивления материалов – одна из геометрических характеристик плоских сечений)

 

Таким образом:

    ,

,

представим величину   - глубина погружения центра тяжести.

Тогда:

;

где   – величина абсолютного гидростатического давления в центре тяжести рассматриваемого сечения.

 

,или  ;

где   – сила, обусловленная атмосферным (поверхностным) давлением.

 – сила, избыточного весового давления жидкости.