1Физические свойства жидкости.
Известно три фазовых состояния веществ: твердое, жидкое, газообразное.
Фазовое состояние определяется силами межмолекулярного взаимодействия.
Жидкое – некоторое промежуточное состояние между твёрдым и газообразным.
Жидкость обладает двумя особыми свойствами:
1. Весьма мало изменяет свой объём при изменении давления или температуры — т.о. сходна с твёрдым телом.
2. обладает текучестью — т.е. не имеет собственной формы (но имеет конечный объём), т.о. сходна с газам.
Эти особые свойства жидкости объясняются её молекулярным строением.
Плотность
жидкости 
где V – рассматриваемый объём жидкости;
m – масса рассматриваемого объёма жидкости.
Объёмный вес жидкости
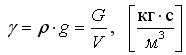(применяется
в технической системе единиц);
. (*)
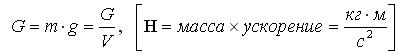Текучесть и вязкость жидкости
Текучесть – свойство жидкости деформироваться под действием сдвиговых напряжений.
Вязкость – свойство текучих тел оказывать сопротивление сдвигающему усилию и препятствовать перемещению одной части объёма относительно другой.
(в некотором роде вязкость – трение внутри объёма жидкости)
2Свойства гидростатического давления.
Свойство 1. Гидростатическое давление всегда направлено по внутренней нормали (т.е. со стороны жидкости) к площадке (рис 2.2 а).
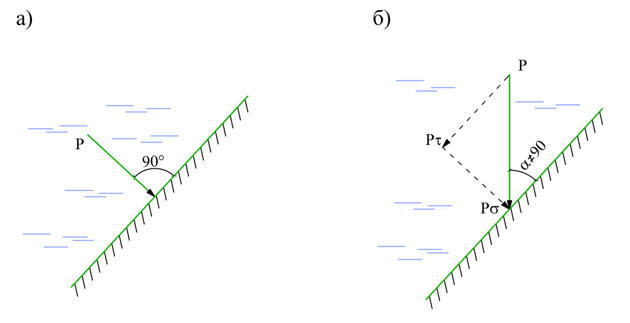
Рис. 2.2 Свойство 1 гидростатического давления.
Свойство 2. Величина гидростатического давления не зависит от ориентации площадки (т.е. гидростатическое давление действует во все стороны).
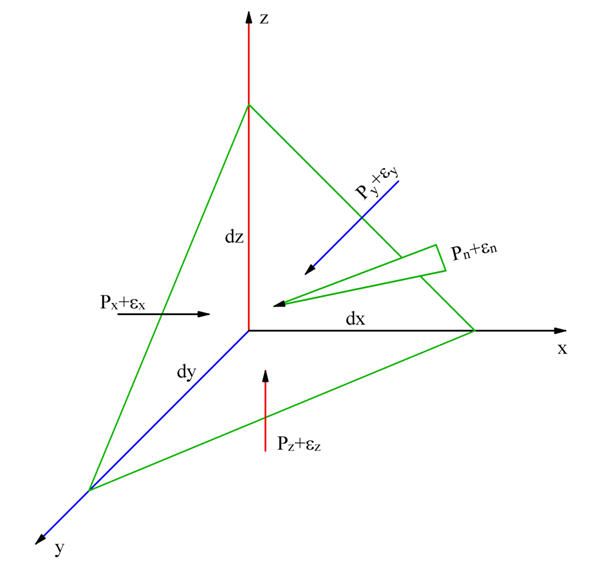
Рис. 2.3 Свойство 2 гидростатического давления.
3 Вывод дифференциальных уравнений покоящейся жидкости.
1. Рассмотрим покоящуюся жидкость, на которую действует массовая сила F (не обязательно сила тяжести).
Отнеся величину силы F к единице массы жидкости, на которую она действует, можно говорить о единичной массовой силе.
(величина силы – скаляр, т.е. длина вектора в масштабе сил)
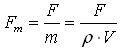(V –
единичный объём, 
)
Так как сила F – вектор можно говорить о проекциях единичной массовой силы Fm
.
2. Выделим в покоящейся жидкости прямоугольный параллелепипед со сторонами dx, dy, dz (Рис. 3.1).
3. Отбросим окружающую параллелепипед жидкость и заменим её действие соответствующими силами – это силы давления, действующие на площадки – грани параллелепипеда.
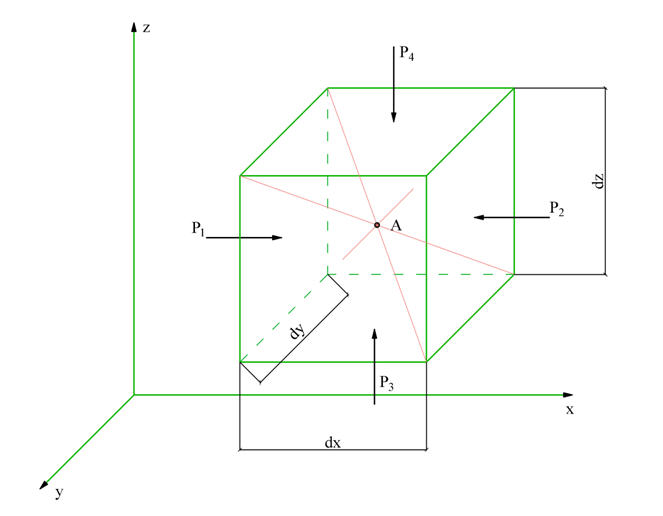
Рис. 3.1. Вывод дифференциальных уравнений покоящейся жидкости.
4. Составим уравнение равновесия для проекций сил:
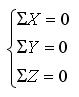
5. Рассмотрим силы давления (поверхностные силы).
Из всех сил давления, действующих на параллелепипед проекции (отличные от нуля) дают только силы Р1 и Р2, причём.
;
,
где р1 и р2 – соответственно, давление в точках приложения сил Р1 и Р2.
Пусть известно давление в точке А (центр параллелепипеда). При действии на жидкость объёмной силы (массовой силы) F давление в ней изменяется по некоторому закону. Опишем это изменение давления с помощью градиента давления.
Градиент давления – величина, характеризующая изменение давления по какому-либо направлению на единице длины.
–
«скорость»
изменения давления в направлении ОХ;
–
«скорость»
изменения давления в направлении ОY;
–
«скорость»
изменения давления в направлении ОZ;
Пусть давление увеличивается вдоль оси ОХ (рис. 3.2), тогда
,
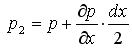
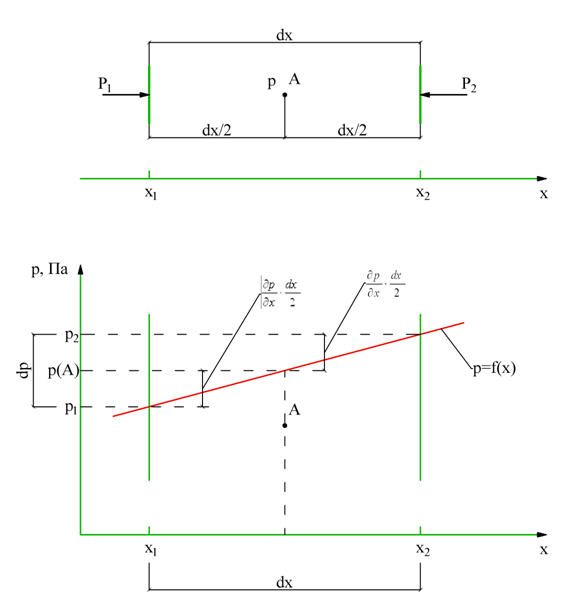
Рис. 3.2. Изменение давления в окрестности точки А.
Градиент
давления – первая производная от функции
изменения давления по соответствующему
направлению (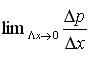 
,
Δр=р2-р1,
Δх=х2-х1).
Если
давление уменьшается вдоль ОХ то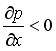 
и
выражения для р1 и
р2 справедливы.
Если
давление – const,
то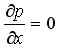 
и
выражения для р1 и
р2 также
справедливы.
6. Рассмотрим массовые силы.
Если известна единичная проекция Х массовой силы F, действующей на жидкость, то для всего элементарного параллелепипеда проекция массовой силы F будет:
,
.
7. Итак, уравнение равновесия в проекции на ОХ.
Действующие силы, дающие проекции (не нулевые): Р1, Р2, Fх.
( Fx прибавляется с учётом её знака)
(подставим значения проекций сил)
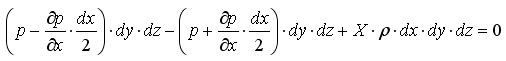
(раскроем скобки)
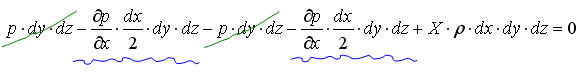
(разделим на объём параллелепипеда)
.
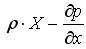8. По аналогии составляя проекции на оси OY и OZ получаем:
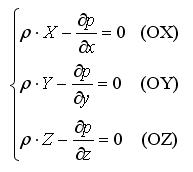
Уравнения Эйлера равновесия покоящейся жидкости