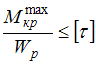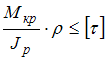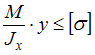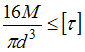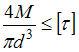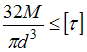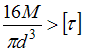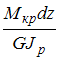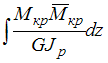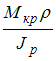Расчет на прочность при кручении.

1. Условие прочности по допускаемым напряжениям при кручении стержня круглого поперечного сечения с неизменным по длине диаметром имеет

2. Из условия прочности, при заданном значении 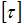, наименьшее допускаемое значение параметра М равно ___.При решении принять .

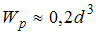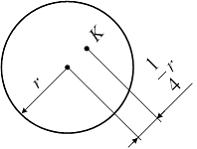
3. Напряжение в точке К опасного поперечного сечения вала (см. рисунок) равно 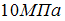. Предел текучести материала вала при сдвиге 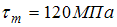. Фактический коэффициент запаса прочности для вала равен …

3

2

12

4

Р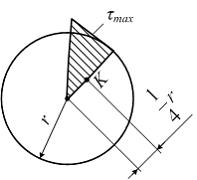 ешение: Закон изменения касательного напряжения вдоль радиуса линейный. Поэтому  а коэффициент запаса прочности для вала

4. Условие прочности по допускаемым напряжениям для ступенчатого вала, изображенного на рисунке, имеет вид ____. Значения М, d и  заданы.

Р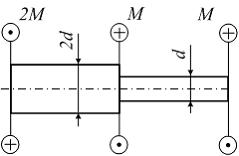 ешение: Формула для максимального напряжения имеет вид  

где  − полярный момент сопротивления. Максимальное касательное напряжение на левом грузовом участке Максимальное касательное напряжение на правом грузовом участке  поэтому условие прочности для вала имеет вид .

4. М_кр − крутящий момент в поперечном сечении круглого вала диаметром d. Напряжение, равное  действует в точке …

D

А

В

С

Решение: При кручении стержня с круглым поперечным сечением касательные напряжения определяются по формул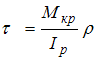е  ; где 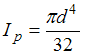 − полярный момент инерции сечения;  − расстояние от оси стержня до точки, в которой определяются касательные напряжения. Меняя в формуле для определения касательного напряжения значение  ρ, получим, что данное значение 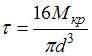 возникает в точке D.

Крутящий момент. Деформации и напряжения

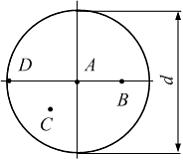
1. Н 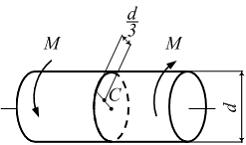апряжение в точке С поперечного сечения равно

Решение: Для определения касательного напряжения используем формулу

 

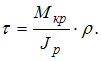
В данном примере М_кр = М,

   

Следовательно,

2. О тносительный угол закручивания определяется по формуле …

или

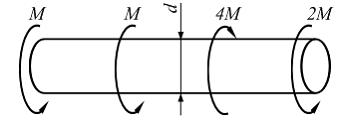
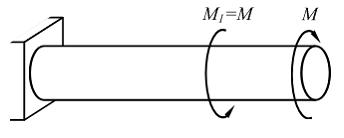
3. При увеличении момента М₁=М в два раза диаметр стержня необходимо …

	оставить неизменным
	увеличить в два раза
	увеличить в четыре раза
	уменьшить в два раза

Р ешение: При увеличении момента М₁ в два раза (см. рисунок) величина максимального крутящего момента  не изменяется, поэтому  не изменятся и диаметр стержня остается неизменным.

4. М_кр − крутящий момент в поперечном сечении круглого вала диаметром d. Напряжение, равное  действует в точке …

D

A

B

C

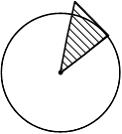
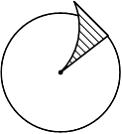
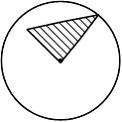
5. При кручении стержня круглого поперечного сечения касательные напряжения изменяются вдоль радиуса, как показано на рисунке …

Решение: Формула для касательного напряжения имеет вид  где − расстояние от центра тяжести поперечного сечения до точки, в которой определяется напряжение. Зависимость  от  − линейная.  

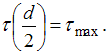
6. При кручении стержня круглого поперечного сечения внутренние силы в поперечном сечении приводятся к …

моменту относительно оси, перпендикулярной к плоскости сечения и проходящей через его центр тяжести

моменту относительно главной центральной оси поперечного сечения

силе, совпадающей с главной центральной осью поперечного сечения

силе, перпендикулярной к плоскости сечения и проходящей через его центр тяжести

Решение: Система внутренних сил в поперечном сечении стержня, на основании положений статики, приводится к центру тяжести сечения. В результате получается главный вектор и главный момент всех внутренних сил. Спроектировав главный вектор и главный момент на оси прямоугольной системы координат, расположенные определенным образом (одна ось направлена по нормали к сечению, а другие расположены в плоскости сечения), получим шесть составляющих: три силы и три момента. Эти составляющие называются внутренними силовыми факторами и имеют определенные наименования. Момент всех внутренних сил относительно оси, перпендикулярной плоскости сечения, называется крутящим моментом. Деформация стержня, когда в поперечном сечении возникает только крутящий момент, называется кручением.