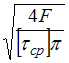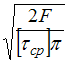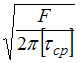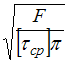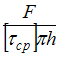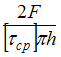Чистый сдвиг. Расчет на сдвиг (срез).

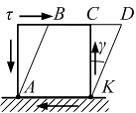
1. Напряженное состояние «чистый сдвиг» показано на рисунке

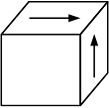
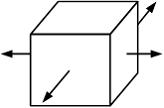
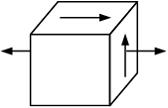
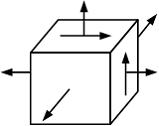
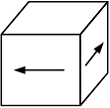
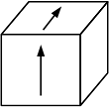
2. Закон парности касательных напряжений при чистом сдвиге показан на рисунке …

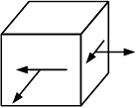
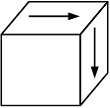
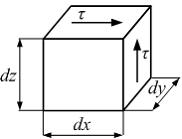
Решение: Выделим из тела бесконечно малый элемент с размерами , ,  Предположим, что на двух гранях элемента возникают только касательные напряжения. Покажем данное напряженное состояние через плоский элемент.   Касательные напряжения, действующие по нижней и верхней грани элемента, образуют пару сил, которая вызывает вращение элемента. Поэтому на боковых гранях элемента возникают такие касательные напряжения, которые должны создавать пару сил противоположного направления. Из условий равновесия следует, что на взаимно перпендикулярных площадках касательные напряжения равны по величине и направлены к общему ребру (или от него). Данное положение называется  законом парности касательных напряжений.

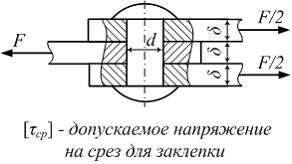
3. Диаметр заклепки из расчета на срез равен …

Р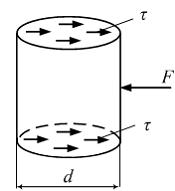 ешение: Рассмотрим равновесие средней части заклепки. Полагаем, что касательные напряжения распределены равномерно по площади поперечного сечения. Условие равновесия имеет вид  откуда  

Условие прочности имеет вид

, тогда

4. И з расчета на срез минимальный диаметр болта при заданных значениях 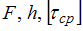 равен …

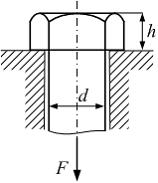
Решение: При определенном значении силы F происходит срез головки болта по цилиндрической поверхности диаметром d. Примем, что касательные напряжения  постоянны по высоте h головки болта. Условие прочности имеет вид , откуда .

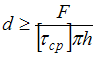5. З акон Гука при сдвиге выражает зависимость между …

	касательным напряжением и углом
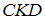
	касательным напряжением и углом
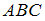
	длиной отрезка 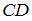 и углом
	касательным напряжением и длиной отрезка

Р ешение Опытные данные показывают, что при небольших напряжениях зависимость между  и  линейная. Эта линейная зависимость называется законом Гука при чистом сдвиге. Аналитически она записывается в виде формулы  где G – коэффициент пропорциональности, называемый модулем упругости при сдвиге (модуль сдвига).

Р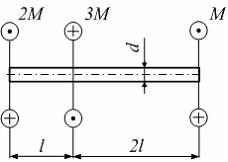 асчет на жесткость при кручении.

1. Стержень круглого сечения диаметром d нагружен, как показано на рисунке. Модуль сдвига материала G, длина l, значение момента М заданы. Взаимный угол поворота крайних сечений равен …

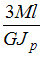
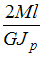
	нулю

Р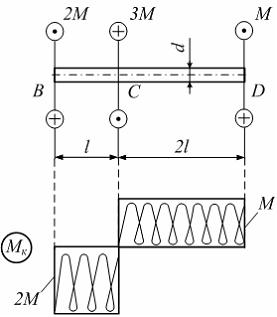 ешение: Сечения, где приложены внешние пары сил, обозначим буквами B, C, D. Построим эпюру крутящих моментов. Угол поворота сечения D относительно сечения B может быть выражен как алгебраическая сумма взаимных углов поворота сечения С относительно сечения B и сечения D относительно сечения С, то есть Взаимный угол поворота двух сечений для стержня с круглым сечением определяется по формуле 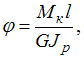 где I_p – полярный момент инерции сечения. Применительно к данной задаче имеем

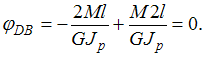
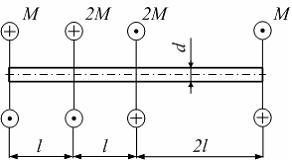2. Стержень круглого сечения диаметром d нагружен, как показано на рисунке. Максимальное значение относительного угла закручивания равно … Модуль сдвига материала G, значение момента М, длина l заданы.

Р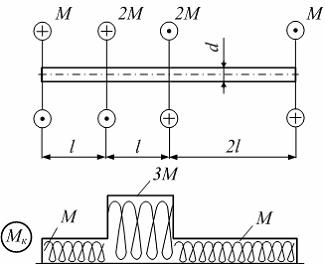 ешение: Построим эпюру крутящих моментов. При решении задачи воспользуемся формулой для определения относительного угла закручивания стержня с круглым поперечным сечением 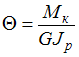. Учитывая, что жесткость поперечного сечения стержня  по длине постоянна, получим .

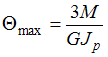3. Выражение 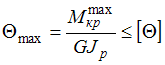 является условием …

   	жесткости для вала с неизменным по длине диаметром
   	жесткости для ступенчатого вала
   	прочности для вала с неизменным по длине диаметром
   	прочности для ступенчатого вала

4. Д ля круглого стержня, работающего на кручение, произведение  называется жесткостью …

	поперечного сечения на кручение
	поперечного сечения на растяжение − сжатие
	поперечного сечения на изгиб
	стержня на кручение

Решение: Относительный угол закручивания стержня круглого поперечного сечения определяется по формуле  

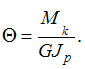
Чем меньше , тем больше жесткость стержня. Поэтому произведение называется жесткостью поперечного сечения стержня на кручение.

5. Выражение  является условием …

	прочности для ступенчатого вала
	жесткости для вала с неизменным по длине диаметром
	жесткости для ступенчатого вала
	прочности для вала с неизменным по длине диаметром