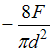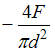Расчеты стержней на прочность и жесткость

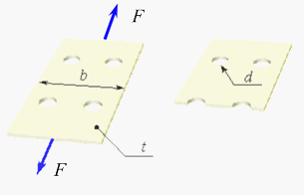
1. Стальной лист с четырьмя отверстиями диаметром 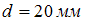 растягивается силами 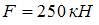. Ширина листа 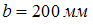, допускаемое напряжение 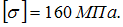 Минимально возможная толщина листа 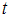 равна _________ см. Концентрацию напряжений не учитывать.

0,97

1,3

1,1

0,78

Решение: Рабочая площадь сечения, ослабленного двумя отверстиями,  Условие прочности имеет вид  откуда .

Минимально возможная толщина листа

2. Стержень квадратного сечения растянут силами F. Если сторону квадрата увеличить в 2 раза, то абсолютное удлинение стержня …

уменьшится в 4 раза

увеличится в 4 раза

уменьшится в 2 раза

увеличится в 2 раза

3. Схема нагружения выполненного из пластичного материала стержня круглого поперечного сечения диаметром d = 5см приведена на рисунке. Фактический коэффициент запаса п 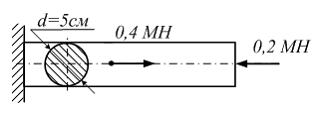рочности должен быть не менее двух. Для этого стержень должен быть изготовлен из материала с пределом текучести не менее ________ МПа.

203,8

150,1

407,6

51,2

4. Стержень с квадратным поперечным сечением а=20см (см. рисунок) нагружен силой 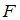. Модуль упругости материала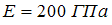 . Допускаемое напряжение 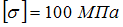. Допустимое перемещение верхнего сечения 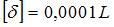. Максимально допустимое значение силы равно _________ МН.

0,8

2,4

4,1

4,8

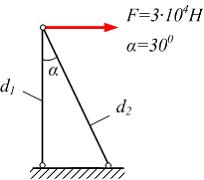5. С хема нагружения фермы показана на рисунке. Допускаемое напряжение [] = 160 МПа. Диаметры поперечных сечений стержней d₁ и d₂ в мм равны …

20,40 и 21,85

10,17 и 10,93

11,74 и 16,60

18,08 и 19,37

Решение: Усилия в стержнях определяются путем вырезания узла А. 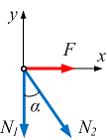Составим сумму проекций всех сил на оси х, у  и приравняем их к нулю. Диаметры стержней определяются из условий прочности: 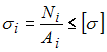. Площади поперечных сечений . Тогда

Продольная сила. Напряжения и деформации

1. Стержень круглого поперечного сечения диаметром d нагружен так, как показано на рисунке. Нормальные напряжения в сечении 1−1 равны …

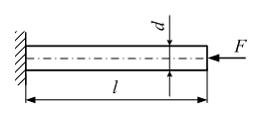2. Д ля стержня круглого поперечного сечения диаметром d, схема которого изображена на рисунке, абсолютное укорочение 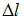 равно _______ . Модуль упругости материала Е задан.

0

Р ешение: Абсолютное укорочение определяется по формуле  

В нашем случае , ,  Площадь сечения . Окончательно .

3. Вдали от мест нагружения характер распределения нормальных напряжений по площади поперечного сечения при растяжении − сжатии зависит от …

статического эквивалента внешней нагрузки

способа приложения внешних сил

величины и способа приложения внешних сил

формы поперечного сечения

Решение: На достаточном удалении от места приложения внешних сил распределение напряжений зависит только от их статического эквивалента (принцип Сен-Венана). От способа приложения внешних сил распределение напряжений зависит существенно лишь вблизи места нагружения.

4. Для стержня, схема которого изображена на рисунке, продольная сила N в сечении 2−2 …

равна нулю

растягивающая и равна F

сжимающая и равна (-F)

сжимающая и равна (3F)

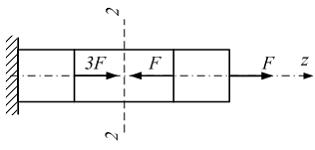
Р ешение: Для определения продольной силы следует рассмотреть равновесие отсеченной правой части стержня  откуда .

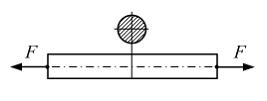5. Н а рисунке показан стержень, растянутый силами . Равномерный характер распределения нормальных напряжений  по площади поперечных сечений (расположенных вдали от точек приложения сил) является следствием …

гипотезы плоских сечений (гипотезы Бернулли)
гипотезы однородности материла
принципа суперпозиции
гипотезы сплошной среды

Р ешение: Гипотеза плоских сечений гласит: «Поперечные сечения стержня, плоские до деформации, остаются плоскими и в процессе деформации». Это означает, что все продольные слои материала между соседними сечениями удлиняются (или укорачиваются) на одну и ту же величину, поэтому напряжения в поперечном сечении распределены по площади сечения равномерно.