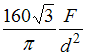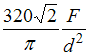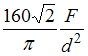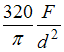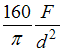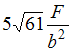- •Основные понятия, определения, допущения и принципы.
- •Внутренние силы и напряжения
- •Виды нагружения стержня.
- •Перемещения и деформации
- •Модели прочностной надежности.
- •Испытание конструкционных материалов на растяжение и сжатие
- •Расчеты стержней на прочность и жесткость
- •Продольная сила. Напряжения и деформации
- •М еханические свойства и механические характеристики материалов
- •Чистый сдвиг. Расчет на сдвиг (срез).
- •Расчет на прочность при кручении.
- •Крутящий момент. Деформации и напряжения
- •Расчет балок на прочность
- •П оперечная сила, изгибающий момент и их эпюры
- •Напряжения в поперечном сечении стержня при плоском изгибе
- •Перемещения при изгибе. Расчет балок на жесткость
- •Изгиб с растяжением - сжатием
- •Изгиб с кручением
- •Пространственный и косой изгиб
Изгиб с кручением
Ломаный стержень круглого сечения диаметром d нагружен внешними силами, как показано на рисунке. Значение эквивалентного напряжения в опасной точке стержня, по теории наибольших касательных напряжений, равно …
|
|
|
|
|
С
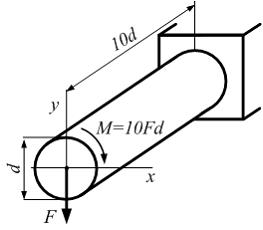 тержень
круглого сечения диаметром
d,
длиной
тержень
круглого сечения диаметром
d,
длиной
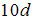 нагружен,
как показано на рисунке. Значение
эквивалентного напряжения в опасной
точке стержня, по теории наибольших
касательных напряжений, равно …
нагружен,
как показано на рисунке. Значение
эквивалентного напряжения в опасной
точке стержня, по теории наибольших
касательных напряжений, равно …
|
|
|
|
|
Р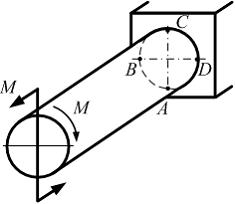 ешение:
Опасное
сечение стержня находится вблизи
заделки, где возникают изгибающий момент
ешение:
Опасное
сечение стержня находится вблизи
заделки, где возникают изгибающий момент
![]() и
крутящий момент
и
крутящий момент
![]() По
теории наибольших касательных напряжений,
По
теории наибольших касательных напряжений,
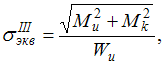 где
где
![]() − осевой
момент сопротивления.
Учитывая, что
− осевой
момент сопротивления.
Учитывая, что
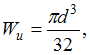 после
преобразований найдем
после
преобразований найдем
![]()
При указанном на рисунке варианте нагружения стержня опасными будут точки …
А иВ
А и D
В иС
В и D
С
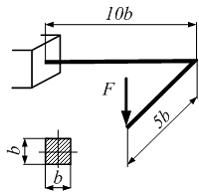 тержень
квадратного поперечного сечения с
размерами
тержень
квадратного поперечного сечения с
размерами
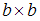 нагружен
силой F.
Значение эквивалентного напряжения
в опасной точке, по теории наибольших
касательных напряжений, равно ___ .
При решении принять
нагружен
силой F.
Значение эквивалентного напряжения
в опасной точке, по теории наибольших
касательных напряжений, равно ___ .
При решении принять
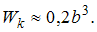
Р ешение:
В сечении вблизи заделки действуют
максимальный изгибающий
ешение:
В сечении вблизи заделки действуют
максимальный изгибающий
![]() и
крутящий
и
крутящий
![]() моменты.
Точки
В
и
С
равноопасны. В точке В
от изгибающего момента возникают
растягивающие нормальные напряжения,
в точке С
– сжимающие. Значение, по абсолютной
величине нормальных напряжений в этих
точках
моменты.
Точки
В
и
С
равноопасны. В точке В
от изгибающего момента возникают
растягивающие нормальные напряжения,
в точке С
– сжимающие. Значение, по абсолютной
величине нормальных напряжений в этих
точках
 Касательные
напряжения в точках В
и С
равны:
Касательные
напряжения в точках В
и С
равны:
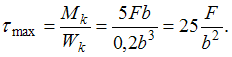 По
теории наибольших касательных напряжений,
эквивалентное напряжение в этих точках
определяется по формуле
По
теории наибольших касательных напряжений,
эквивалентное напряжение в этих точках
определяется по формуле
![]() После
подстановки значений
После
подстановки значений
![]() и
и
![]() найдем
найдем
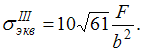
Пространственный и косой изгиб
При косом изгибе нейтральная линия в поперечном сечении стержня проходит …
-
через центр тяжести сечения и в общем случае не перпендикулярна к плоскости действия изгибающего момента
через центр тяжести сечения и перпендикулярна к плоскости действия изгибающего момента
перпендикулярна к плоскости действия изгибающего момента и не проходит через центр тяжести сечения
не перпендикулярна к плоскости действия изгибающего момента и не проходит через центр тяжести сечения
Решение:
Уравнение
нейтральной линии при косом изгибе
получим из формулы для определения
нормального напряжения в произвольной
точке сечения, полагая
![]() .
Тогда
.
Тогда
![]() где
где
![]() –
координаты точек нейтральной линии.
После преобразований найдем
–
координаты точек нейтральной линии.
После преобразований найдем
![]() Имеем
уравнение прямой, проходящей через
начало координат. Угол
Имеем
уравнение прямой, проходящей через
начало координат. Угол
![]() ,
угол наклона нейтральной линии, при
,
угол наклона нейтральной линии, при
![]() не
перпендикулярен к плоскости действия
изгибающего момента. Условие
перпендикулярности двух прямых
определяется равенством
не
перпендикулярен к плоскости действия
изгибающего момента. Условие
перпендикулярности двух прямых
определяется равенством
![]() .
Следовательно, при косом изгибе
нейтральная линия проходит через центр
тяжести сечения и не перпендикулярна
к плоскости действия изгибающего
момента.
.
Следовательно, при косом изгибе
нейтральная линия проходит через центр
тяжести сечения и не перпендикулярна
к плоскости действия изгибающего
момента.
П
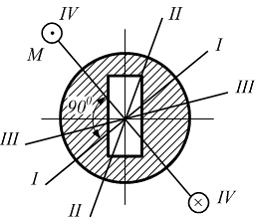 лоскость
действия изгибающего момента в поперечном
сечении стержня показана на рисунке.
Примерное положение нейтральной линии
в данном сечении совпадает с прямой …
лоскость
действия изгибающего момента в поперечном
сечении стержня показана на рисунке.
Примерное положение нейтральной линии
в данном сечении совпадает с прямой …
-
III - III
II - II
I - I
IV - IV
Решение: Нейтральная линия в поперечном сечении стержня проходит через центр тяжести сечения, не перпендикулярна силовой плоскости (плоскости действия момента) и несколько повернута в сторону главной центральной оси с минимальным моментом инерции.
С
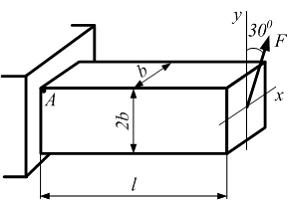 тержень
длиной
прямоугольного
сечения с размерами
тержень
длиной
прямоугольного
сечения с размерами
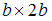 нагружен
силой F,
лежащей в плоскости сечения. Значение
нормального напряжения в точке А
равно …
нагружен
силой F,
лежащей в плоскости сечения. Значение
нормального напряжения в точке А
равно …
-
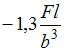
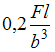 ;
;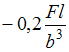 ;
;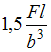
Решение:
В
поперечном сечении стержня вблизи
заделки возникают изгибающие моменты:
![]() ,
,
![]() От
действия изгибающего момента
в
точке А
возникает сжимающее напряжение, от
момента
От
действия изгибающего момента
в
точке А
возникает сжимающее напряжение, от
момента
![]() − растягивающее.
Следовательно,
− растягивающее.
Следовательно,
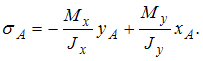 где
где
![]() − осевые
моменты инерции сечения относительно
главных центральных осей;
− осевые
моменты инерции сечения относительно
главных центральных осей;
![]() − координаты
точки
А
в системе главных центральных осей,
взятые по абсолютной величине. При
заданных размерах поперечного
сечения
− координаты
точки
А
в системе главных центральных осей,
взятые по абсолютной величине. При
заданных размерах поперечного
сечения
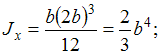
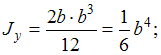
![]()
![]() Подставим
полученные значения в формулу для
определения нормального напряжения,
получим
Подставим
полученные значения в формулу для
определения нормального напряжения,
получим
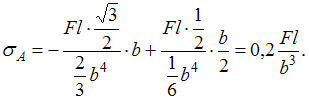
П
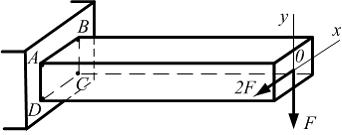 ри
данном варианте нагружения стержня
максимальные нормальные напряжения
возникают в точке …
ри
данном варианте нагружения стержня
максимальные нормальные напряжения
возникают в точке …
-
D
А
В
С
Изгиб, при котором плоскость действия изгибающего момента не совпадает с главными центральными плоскостями стержня, называют …
-
косым
плоским
поперечным
чистым