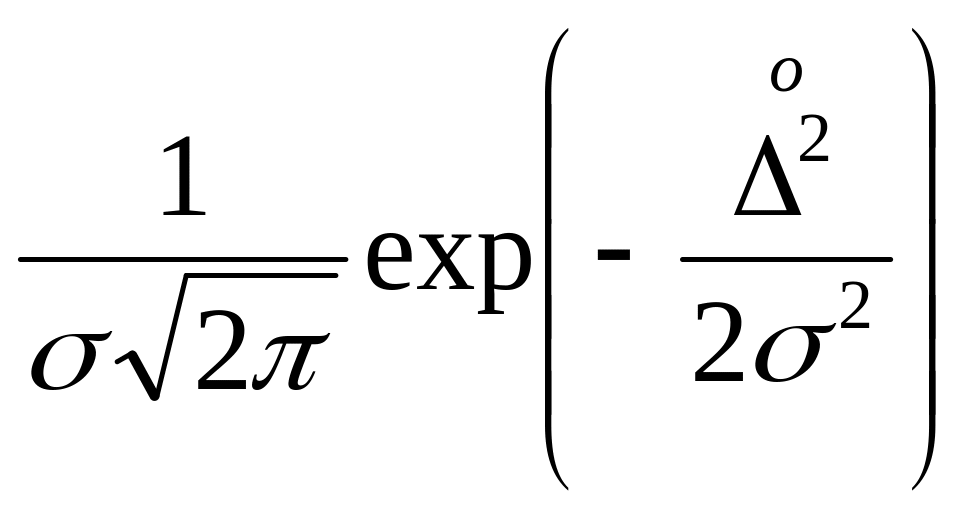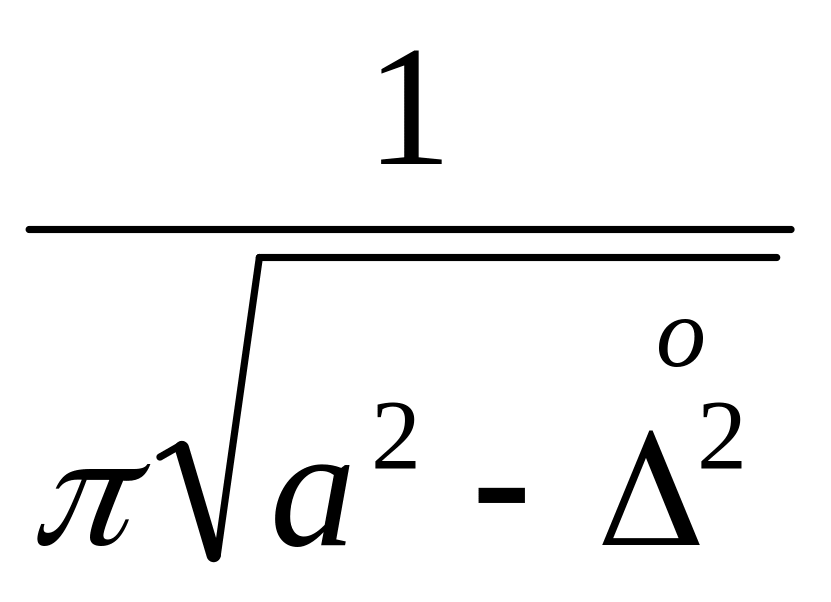3.4 Случайные погрешности

Случайная погрешность измерения или, точнее, случайная составляющая погрешности результата измерения – погрешность, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же, неизменной физической величины, проведённых с одинаковой тщательностью по одной и той же методике, одним и тем же средством измерений и в одних и тех же условиях. Причиной появления случайных погрешностей является нестабильность процессов, происходящих в средствах измерений и вспомогательном оборудовании, а также в действиях оператора, выполняющего измерения. Нестабильность эта скрытая и не устранимая при проведении самих измерений. Примерами такой нестабильности являются: трение и люфты в опорах механических узлов, гистерезис в электрических и магнитных цепях, тепловые шумы в электронных узлах, изменения условий измерений случайного характера, дискретность отсчёта показаний и др.

Случайные погрешности вызывают рассеяние результатов в ряду следующих друг за другом отдельных измерений и ведут себя как случайные, вероятностные величины. Поэтому в качестве математической базы их рассмотрения и исследования применяется теория вероятности. В общем случае случайные погрешности характеризуются следующими двумя особенностями, вытекающими из теории вероятности:

- при большом числе измерений случайные погрешности одинакового значения, но разного знака встречаются одинаково часто (симметричность рассеяния);

- большие (по модулю) погрешности встречаются реже, чем меньшие.

Наглядно это можно проиллюстрировать на графике (рис. 3.1), где – случайная погрешность, – плотность распределения вероятностей случайных погрешностей.

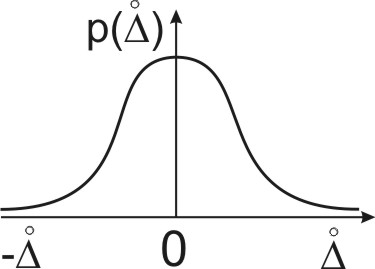
Рисунок 3.1 – График распределения случайных погрешностей

Случайная погрешность на первый взгляд представляется более неприятной, чем систематическая. Однако, для борьбы с ней (уменьшение и даже исключение) есть универсальный и эффективный способ – статистическая обработка результатов измерений. Правда, способ этот трудоёмкий, поскольку требует проведения нескольких измерений одной и той же величины, и чем больше, тем лучше, т.е. требуется проведение многократных измерений. В этом случае результатом измерения является среднее арифметическое значение результатов отдельных измерений, которое определяется по формуле

(3.1)

где – среднее арифметическое значение;

– значение результата i-го измерения;

n – количество единичных (отдельных) измерений в ряду.

При этом результаты отдельных измерений будут случайным образом рассеяны около среднего арифметического значения, а разность между ними и средним арифметическим значением является случайной абсолютной погрешностью измерения _i, т.е.

_i = Q_i – . (3.2)

Для оценки случайных погрешностей используют ряд статистических величин; чаще всего это размах результатов измерений R и среднее квадратическое отклонение σ (СКО).

Размах результатов измерений вычисляется по формуле

,

где Q_max и Q_min – наибольшее и наименьшее значения результатов измерений в данном ряду.

Среднее квадратическое отклонение (СКО) σ определяется выражением

при n → ∞. (3.3)

При конечном числе измерений подобным образом определяется оценка СКО S, которая в данном случае может быть названа средней квадратической погрешностью отдельных измерений, определяемой по уточнённой формуле

S = 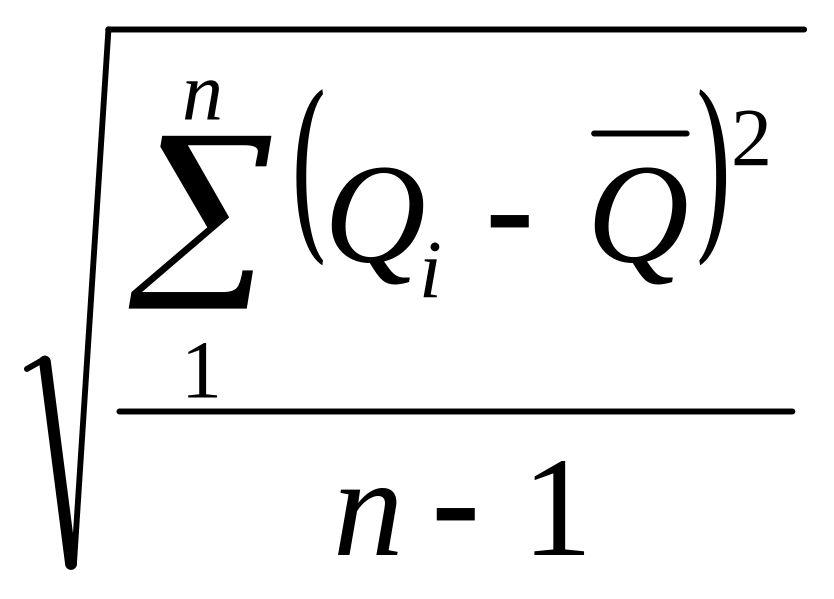. (3.4)

На практике зачастую не делают различия между СКО σ и её оценкой S, что не вполне корректно.

Средняя квадратическая погрешность – это некая усредненная случайная погрешность, ограничивающая интервал (±S), в который попадает определённая часть из всех отдельных погрешностей, например, при нормальном законе распределения – 0,68, а при равномерном – 0,58.

Статистические достоверность и надёжность средней квадратической погрешности повышаются с увеличением количества единичных измерений; практически уже при n ≥ 30 они достигают предельных уровней, а при n < 10 становятся кране низкими, и проводить многократные измерения не имеет смысла.

Согласно теории вероятностей среднее арифметическое значение при конечном числе измерений остаётся также случайной величиной, однако его рассеяние и, соответственно, его случайная погрешность будет значительно меньше, чем у результатов отдельных, единичных измерений. Это является результатом частичной компенсации отдельных погрешностей друг друга, имеющих разные знаки. При этом оказывается, что средняя квадратическая погрешность среднего арифметического значения S и средняя квадратическая погрешность отдельных измерений S связаны между собой формулой

S = = 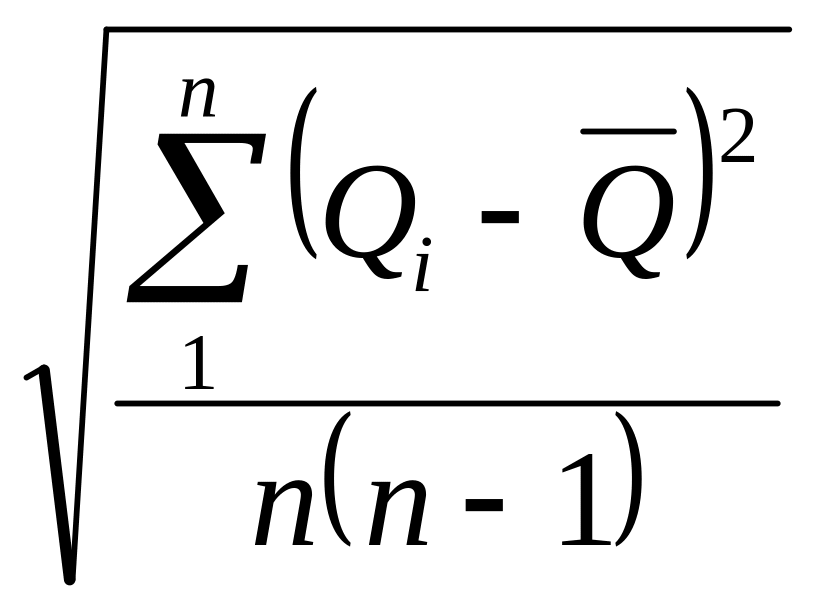. (3.5)

Из данного выражения следует, что при достаточно большом количестве измерений (n→ ∞) средняя квадратическая погрешность среднего арифметического значения (результата многократных измерений) становится пренебрежимо малой (стремится к нулю).

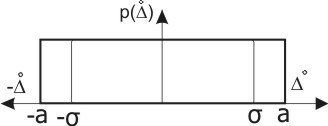
Результаты обработки многократных измерений, в том числе расчёт случайных погрешностей, зависят от характера распределения результатов единичных измерений в данном ряду, выражаемого в виде закона распределения (рассеяния) их как величин случайных. В измерительной практике случайные погрешности наиболее часто подчиняются таким законам как равномерный, трапецеидальный, нормальный, двухмодальный. Графики и некоторые характеристики этих законов представлены в таблице 3.1.

Таблица 3.1

Наименование закона	График	Плотность распределения вероятности р(Δ)	Среднее квадратическое отклонение σ	Доверительная вероятность в интерва-ле ±σ
Равномерный				0,58
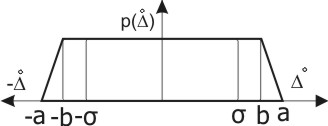
Трапецеидальный				0,59 при а=1,5b
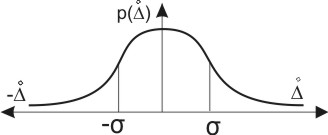
Нормальный				0,68
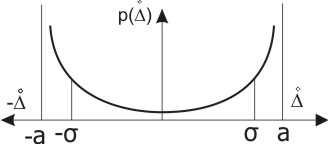
Двухмодальный (арксинусоидальный)				0,5

С учётом сказанного оценки S и S ещё не принимаются в качестве окончательных случайных погрешностей, поскольку вероятность выхода фактической случайной погрешности результата отдельного измерения или среднего арифметического значения за соответствующие пределы (±S или ± S ) может оказаться более 0,3 или даже 0,5, что с точки зрения обеспечения достоверности результатов измерений не приемлемо. Поэтому за итоговую оценку случайной погрешности принимается доверительный интервал, границы (их две – нижняя и верхняя) которого определяются в зависимости от рассчитанного значения средней квадратической погрешности и заданной (выбранной) доверительной вероятности Р_д по специальным вероятностным таблицам для установленного закона распределения (для нормального закона – это интегральная функция Лапласа). Доверительная вероятность выбирается субъектом измерений в соответствии с поставленной измерительной задачей (надёжности оценки измеряемой величины), и в практике измерений принимается равной 0,9 – для неответственных измерений, 0,95 – для рядовых массовых измерений, 0,99 – для ответственных измерений.

Непосредственно по таблице находится аргумент функции Лапласа z_p для принятой доверительной вероятности, а границы доверительного интервала рассчитываются по формулам:

D_p = ± z_p S – для случайной погрешности отдельных измерений и

D_p = ± z_p S – для случайной погрешности среднего арифметического значения.

Так, например, при вероятности Р_д = 0,95 аргумент составляет z_p = 1,96, а при Р_д = 0,99 z_p = 2,58. Чем выше доверительная вероятность, тем шире доверительный интервал случайной погрешности.

Рассмотренный способ нахождения доверительных интервалов справедлив при достаточно большом числе отдельных измерений, практически при n ≥ 30, когда можно принять, что S ≈ σ. В случае n < 30 (частый в практике измерений) расчёт доверительных интервалов проводится с использованием специального распределения случайной величины – распределения Стьюдента. Границы доверительного интервала вычисляются по аналогичным формулам:

D_p = ±t_pS или D_p = ±t_p S , (3.6)

где t_p – коэффициент Стьюдента.

Значения коэффициента Стьюдента зависят от числа отдельных измерений n и заданной (выбранной) доверительной вероятности Р_д, определяются методами теории вероятности и для практического применения даются в виде специальной таблицы. Фрагмент такой таблицы, достаточный для выполнения расчётов случайных погрешностей, дан в виде таблицы 3.2.

Таблица 3.2

Рд	n
	7	10	15	20	30	∞
0,8	1,44	1,38	1,35	1,33	1,3	1,28
0,9	1,94	1,83	1,76	1,73	1,7	1,64
0,95	2,45	2,26	2,14	2,09	2,04	1,96
0,99	3,71	3,25	2,98	2,86	2,75	2,58

Строго говоря, указанные коэффициенты Стьюдента соответствуют определённому закону распределения случайных погрешностей, а именно, нормальному. Поэтому необходимо убедиться, что в конкретном случае распределение погрешностей близко к нормальному закону. В противном случае в расчёты надо будет вносить поправки (в теории вероятности они известны). Наиболее простой и наглядный способ определения вида распределения случайной погрешности – графический, заключающийся в построении гистограммы.

Гистограмма строится следующим образом. Весь массив (выборка) случайных погрешностей, полученных при данных многократных измерениях, распределяется в ряд от максимальной отрицательной до максимальной положительной. Далее этот интервал разбивается на 8 – 12 более мелких и равных интервалов, имеющих, по возможности, «круглое» значение. Затем эти малые интервалы наносятся на ось абсцисс в приемлемом и удобном масштабе, а по оси ординат откладывается шкала числа измерений (в пределах 0 – n/3). Над каждым малым интервалом строится столбик высотой, равной числу погрешностей, значения которых попадают в данный интервал. Полученная таким образом диаграмма и будет представлять собой гистограмму.

Проведя через середины вершин столбцов плавную кривую, получают график распределения случайных погрешностей, который можно соотнести с графиком того или иного закона распределения случайных величин. Пример (абстрактный) гистограммы приведён на рисунке 3.1, из которого можно заключить, что данное распределение случайных погрешностей близко к нормальному.

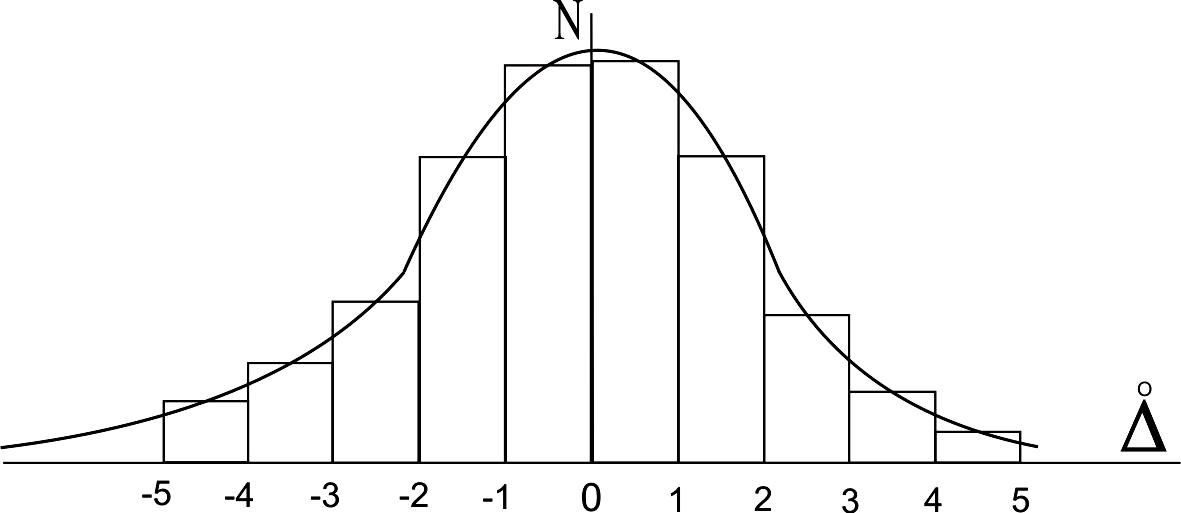
Рисунок 3.2 – Гистограмма

Из сказанного о случайных погрешностях следует, что их уменьшение, минимизация возможно двумя путями: статистическим и совершенствованием методов и средств измерений. Первый путь требует большого объёма измерений, что порой невозможно физически или не приемлемо по другим причинам, и полностью ложится на плечи субъекта измерений (пользователя средством измерений). Второй путь – это уже забота разработчиков средств измерений, и этот путь приносил плоды до сих пор и будет приносить их впредь. У большинства современных типов рабочих средств измерений случайная составляющая погрешности сведена до пренебрежимо малого уровня и, в силу этого, даже не нормируется. Второй путь тем более важен, что основная масса рабочих измерений – это однократные или непрерывные измерения, когда многократные измерения неизменной величины невозможны или неоправданны.