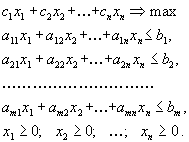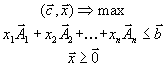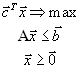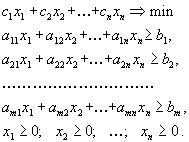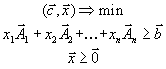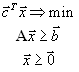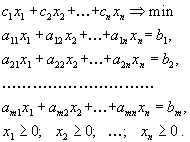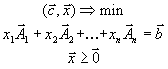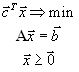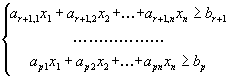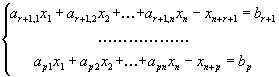Билет 1. Общая Задача Линейного Программирования

Линейное программирование - это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать

Общая задача линейного программирования

Формулировка задачи.

Дана линейная функция

(1.1)    Z = С ₁ х ₁ +С ₂ х ₂ +... +С _N x _N

и система линейных ограничений

a ₁₁ x ₁ + a ₂₂ x ₂ + ... + a _1N Х _N = b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ + ... + a _2N Х _N = b ₂

. . . . . . . . . . .

a _i1 x ₁ + a _i2 x ₂ + ... + a _iN Х _N = b _i (1.2)

. . . . . . . . . . .

a _M1 x ₁ + a _M2 x ₂ + ... + a _MN Х _N = b _M

(1.3)                x _j 0 (j = 1, 2, ... ,n)

где а _ij , Ь _j и С _j - заданные постоянные величины.

Найти такие неотрицательные значения х ₁ , х ₂ , ..., х _n , которые удовлетворяют системе ограничений (1.2) и доставляют линейной функции (1.1)минимальное значение.

Общая задача имеет несколько форм записи

Векторная форма записи. Минимизировать линейную функцию Z = СХ при ограничениях

(1.4)                            А ₁ х ₁ + А ₂ x ₂ + ... + А _N x _N = А _о , X 0

где С = (с ₁ , с ₂ , ..., с _N ); Х = (х ₁ , х ₂ , ..., х _N ); СХ - скалярное произведение; векторы

A ₁ , A ₂ ,..., A _N , A ₀

состоят соответственно из коэффициентов при неизвестных и свободных членах

Матричная форма записи . Минимизировать линейную функцию, Z = СХ при ограничениях АХ = А ₀ , Х 0, где С = (с ₁ , с ₂ , ..., с _N ) - матрица-cтрока; А = (а _ij ) - матрица системы;

Х - матрица-столбец, А ₀ - матрица-столбец

Запись с помощью знаков суммирования. Минимизировать линейную функцию Z = С _j х _j при ограничениях

0пределение 1. Планом или допустимым решением задачи линейного программирования называется Х = (х ₁ , х ₂ , ..., х _N ), удовлетворяющий условиям (1.2) и (1.3)

0пределение 2. План Х = (х ₁ , х ₂ , ..., х _N ) называется опорным, если векторы А (i = 1, 2, ..., N), входящие в разложение (1.4) с положительными коэффициентами х , являются линейно независимыми

Так как векторы А являются N-мерными, то из определения опорного плана следует, что число его положительных компонент не может превышать М

0пределение 3. Опорный план называется невырожденным, если он содержит М положительных компонент, в противном случае опорный план называется вырожденным

0пределение 4 . Оптимальным планом или оптимальным решением задачи линейного программирования называется план, доставляющий наименьшее (наибольшее) значение линейной функции

В дальнейшем рассмотрено решение задач линейного программирования, связанных с нахождением минимального значения линейной функции. Там, где необходимо найти максимальное значение линейной функции, достаточно заменить на противоположный знак линейной функции и найти минимальное значение последней функции. Заменяя на противоположный знак полученного минимального значения, определяем максимальное значение исходной линейной функции

Множество Допустимых Решений Задач Линейного Программирования

Далее приведем примеры некоторых типовых задач, решаемых при помощи методов линейного программирования. Такие задачи имеют реальное экономическое содержание. Сейчас лишь сформулируем их в терминах ЗЛП, а методы решения подобных задач рассмотрим ниже.

1. Задача об оптимальном использовании ресурсов при производственном планировании. Общий смысл задач этого класса сводится к следующему. Предприятие выпускает n различных изделий. Для их производства требуется m различных видов ресурсов (сырья, материалов, рабочего времени и т.п.). Ресурсы ограничены, их запасы в планируемый период составляют, соответственно, b₁, b₂,..., b_m условных единиц. Известны также технологические коэффициенты a_ij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы изделия j-го вида (   ). Прибыль, получаемая предприятием при реализации изделия j-го вида, равна c_j. В планируемом периоде значения величин a_ij, b_i и c_jостаются постоянными. Требуется составить такой план выпуска продукции, при реализации которого прибыль преприятия была бы наибольшей. Далее приведем простой пример задачи такого класса.

Компания специализируется на выпуске хоккейных клюшек и наборов шахмат. Каждая клюшка приносит компании прибыль в размере $2, а каждый шахматный набор - в размере $4. На изготовление одной клюшки требуется четыре часа работы на участке A и два часа работы на участке B. Шахматный набор изготавливается с затратами шести часов на участке A, шести часов на участке B и одного часа на участке C. Доступная производственная мощность участка A составляет 120 н-часов в день, участка В - 72 н-часа и участка С - 10 н-часов. Сколько клюшек и шахматных наборов должна выпускать компания ежедневно, чтобы получать максимальную прибыль?

Условия задач указанного класса часто представляют в табличной форме (см. таблицу 2.1).

производственные участки	затраты времени на единицу продукции, н-час		доступный фонд времени, н-час
	клюшки	наборы шахмат
А	4	6	120
В	2	6	72
С	-	1	10
прибыль на единицу продукции, $	2	4

По данному условию сформулируем задачу линейного программирования. Обозначим: x₁ - количество выпускаемых ежедневно хоккейных клюшек, x₂ - количество выпускаемых ежедневно шахматных наборов. Формулировка ЗЛП:

= 2x1 + 4x2 → max;
4x1 + 6x2 ≤ 120, 2x1 + 6x2 ≤ 72, x2 ≤ 10;
x1 ≥ 0,   x2 ≥ 0.

Подчеркнем, что каждое неравенство в системе функциональных ограничений соответствует в данном случае тому или иному производственному участку, а именно: первое - участку А, второе - участку В, третье - участку С. Повторимся, методы решения ЗЛП мы будем рассматривать чуть позднее, а сейчас - пример задачи другого типа.

2. Задача о смесях (планирование состава продукции). К группе задач о смесях относят задачи по отысканию наиболее дешевого набора из определенных исходных материалов, обеспечивающих получение смеси с заданными свойствами. Иными словами, получаемые смеси должны иметь в своем составе m различных компонентов в определенных количествах, а сами компоненты являются составными частями n исходных материалов.

На птицеферме употребляются два вида кормов - I и II. В единице массы корма I содержатся единица вещества A, единица вещества В и единица вещества С. В единице массы корма II содержатся четыре единицы вещества А, две единицы вещества В и не содержится вещество C. В дневной рацион каждой птицы надо включить не менее единицы вещества А, не менее четырех единиц вещества В и не менее единицы вещества С. Цена единицы массы корма I составляет 3 рубля, корма II - 2 рубля. Составьте ежедневный рацион кормления птицы так, чтобы обеспечить наиболее дешевый рацион. Представим условие задачи в таблице 2.2.

питательные вещества	содержание веществ в единице массы корма, ед.		требуемое количество в смеси, ед.
	корм I	корм II
А	1	4	1
В	1	2	4
С	1	-	1
цена единицы массы корма, р	2	4

Cформулируем задачу линейного программирования. Обозначим: x₁ - количество корма I в дневном рационе птицы, x₂ - количество корма II в дневном рационе птицы. Формулировка ЗЛП:

= 3x1 + 2x2 → min;
x1 + 4x2 ≥ 1, x1 + 2x2 ≥ 4, x1 ≥ 1;
x1 ≥ 0,   x2 ≥ 0.

3. Транспортная задача. Под транспортной задачей понимают целый ряд задач, имеющих определенную специфическую структуру. Наиболее простыми транспортными задачами являются задачи о перевозках некоторого продукта из пунктов отправления в пункты назначения при минимальных затратах на перевозку.

Три поставщика одного и того же продукта располагают в планируемый период следующими его запасами: первый – 120 условных единиц, второй – 100 условных единиц, третий – 80 условных единиц. Этот продукт должен быть перевезен к трем потребителям, потребности которых равны 90, 90 и 120 условных единиц, соответственно. Обычно начальные условия транспортной задачи записывают в так называемую транспортную таблицу (см. таблицу 2.3). В ячейках таблицы в левом верхнем углу записывают показатели затрат (расходы по доставке единицы продукта между соответствующими пунктами), под диагональю каждой ячейки размещается величина поставки x_ij (т.е. x_ij - количество единиц груза, которое будет перевезено от i-го поставщика j-му потребителю).

Необходимо определить наиболее дешевый вариант перевозок, при этом каждый поставщик должен отправить столько груза, сколько имеется у него в запасе, а каждый потребитель должен получить нужное ему количество продукции. Сформулируем ЗЛП:

= 7x11 + 6x12 + 4x13 + 3x21 + 8x22 + 5x23 + 2x31 + 3x32 + 7x33 → min;
x11 + x12 + x13 = 120, x21 + x22 + x23 = 100, x31 + x32 + x33 = 80, x11 + x21 + x31 = 90, x12 + x22 + x32 = 90, x13 + x23 + x33 = 120;
xij ≥ 0,   ( ,  ).

  Геометрическое решение ЗЛП

Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Таким образом, данный метод решения ЗЛП имеет очень узкие рамки применения. Однако метод представляет большой интерес с точки зрения выработки наглядных представлений о сущности задач линейного программирования. Геометрический (или графический) метод предполагает последовательное выполнение ряда шагов. Ниже представлен порядок решения задачи линейного программирования на основе ее геометрической интерпретации.

1. Сформулировать ЗЛП.

2. Построить на плоскости {х₁, х₂} прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

3. Найти полуплоскости, определяемые каждым из ограничений задачи.

4. Найти область допустимых решений.

5. Построить прямую c₁x₁ + c₂x₂ = h, где h - любое положительное число, желательно такое, чтобы проведенная прямая проходила через многоугольник решений.

6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. В результате, либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции на множестве решений.

7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке.

Далее рассмотрим пример решения ЗЛП графическим методом. Для этого воспользуемся представленной выше задачей о хоккейных клюшках и шахматных наборах.

Основные теоремы линейного программирования

Для обоснования методов решения задач линейного программирования сформулируем ряд важнейших теорем, опуская их аналитические доказательства. Уяснить смысл каждой из теорем поможет понятие о геометрической интерпретации решения ЗЛП, данное в предыдущем подразделе. Однако сначала напомним о некоторых понятиях, важных с точки зрения дальнейшего разговора. Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные m-n переменных называются неосновными (или свободными). Базисным решением системы m линейных уравнений c n переменными (m < n) называется всякое ее решение, в котором все неосновные переменные имеют нулевые значения.

Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым. В частном случае, когда в систему ограничений входят только две переменные x₁ и x₂, это множество можно изобразить на плоскости. Так как речь идет о допустимых решениях (x₁, x₂ ≥ 0), то соответствующее множество будет располагаться в первой четверти декартовой системы координат. Это множество может быть замкнутым (многоугольник), незамкнутым (неограниченная многогранная область), состоять из единственной точки и, наконец, система ограничений-неравенств может быть противоречивой.

Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с одной (двумя) из угловых точек множества допустимых решений. Из теоремы 2 можно сделать вывод о том, что единственность оптимального решения может нарушаться, причем, если решение не единственное, то таких оптимальных решений будет бесчисленное множество (все точки отрезка, соединяющего соответствующие угловые точки).

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений, и наоборот. Следствием из теорем 2 и 3 является утверждение о том, что оптимальное решение (оптимальные решения) задачи линейного программирования, заданной (или приведенной) ограничениями-уравнениями, совпадает с допустимым базисным решением (допустимыми базисными решениями) системы ограничений. Таким образом, оптимальное решение ЗЛП следует искать среди конечного числа допустимых базисных решений.

 Математическая модель задачи линейного программирования. Перед решением задачи составляем её математическую модель.

Математическая модель – это совокупность соотношений, состоящих из линейной целевой функции и линейных ограничений на переменную.

Принцип составления математической модели.

Выбирают переменные задачи.

Переменными задачи называются величины   которые полностью характеризуют экономический процесс, описанный в задачи. Обычно записываются в виде вектора X = ( ). Причём  )

Составляют систему ограничения задачи.

Система ограничений – это совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которая следует из ограниченности экономических условий задачи.

В общем виде система записывается в виде

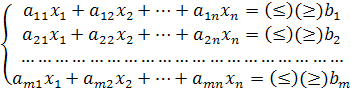
Задают целевую функцию.

Целевая функция – это функция Z(X) которая характеризует качество выполнения задачи, экстремум которой надо найти. В общем виде целевая функция записывается Z(X) =   (max, min)

т.о. математическая модель имеет вид найти переменные задачи   удовлетворяющие системе ограничений:

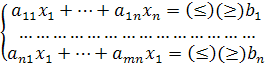
и условию неотрицательности     0 (j =  ), которая обеспечивает экстремум целевой функции Z(Y) =

Допустимым решением задачи линейного программирования называется любой набор значений переменных удовлетворяющий системе ограничений и условной неотрицательности.

Множество допустимых решений образует область допустимых решений задачи (ОДР).

Оптимальным решением называется допустимое решение задачи, при котором целевая функция достигает экстремума.

Билет 2. Каноническая форма задачи линейного программирования

Математическая модель задачи должна иметь каноническую форму.

Если система ограничения состоит только из уравнения и все переменные удовлетворяют условию неотрицательности, то задача имеет каноническую форму.

Если в системе есть хотя бы одно неравенство или какая–либо переменная, неограниченная условием неотрицательности, то задача имеет стандартную форму. Чтобы привести задачу к каноническому виду надо:

перейти от неравенств к уравнению следующим образом: в левую часть неравенств вводим дополнительную переменную с коэффициентом (+1) для неравенства ( ) и (-1) для неравенства ( ) дополнительные переменные не наложены целевые неотрицательности, то её заменяют разностью двух неотрицательных переменных, то есть:

 =   –   (

Общий вид канонической формы:

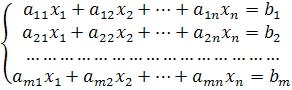
Первая стандартная форма задачи линейного программирования имеет вид

(1.7)

Введем вектора

;   ;   ,

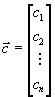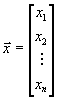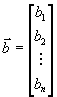a также вектора

, 

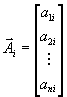и матрицу

 .

Заметим, что комбинация   есть не что иное, как скалярное произведение векторов   и   . Поэтому в векторной форме задача (1.7)примет вид

(1.8)

Можно использовать и матричные обозначения. Тогда комбинация

есть произведение

и задача (1.7) примет вид

(1.9)

Вторая стандартная форма задачи линейного программирования имеет вид

(1.10)

В векторной форме эта задача имеет вид

(1.11)

и в матричной форме - вид

(1.12)

Канонической формой задачи линейного программирования называется задача вида

(1.13)

В векторной форме эта задача имеет вид

(1.14)

 

и в матричной форме - вид

(1.15)

Во всех этих задачах функцию   называют целевой функцией.Вектор   называют вектором коэффициентовлинейной формы, вектор    вектором ограничений.

Матрицу

называют матрицей коэффициентов.

Любой набор чисел   , удовлетворяющий ограничениям задачи, называют планом, а множество всех планов  допустимой областью. Тот план, который доставляет экстремум (минимум или максимум) целевой функции, называют оптимальным планом или просто решением задачи линейного программирования.

Правила приведения задач линейного программирования к стандартной и канонической формам

Рассмотрим теперь те приёмы, которые позволяют произвольные формы задач линейного программирования приводить к указанным выше стандартным формам.

1. Превращение max в min и наоборот.

Если целевая функция в задаче линейного программирования задана в виде

 ,

то, умножая её на (- 1), приведем её к виду

 ,

так как смена знака приводит к смене

на   .

Аналогично можно заменить

на  .

2. Смена знака неравенства.

Если ограничение задано в виде

 ,

то, умножая на (- 1), получим:

 .

Аналогично, неравенство вида больше либо равно можно превратить в неравенство вида меньше либо равно .

3. Превращение равенства в систему неравенств.

Если ограничение задано в виде

 ,

то его можно заменить эквивалентной системой двух неравенств

 ,

 ,

или такой же системой неравенств со знаками больше либо равно .

Указанные выше приемы позволяют приводить задачи линейного программирования к стандартной форме.

4. Превращение неравенств в равенства.

Пусть исходная форма задачи линейного программирования имеет вид

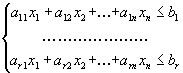
(1.16)

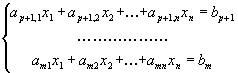
Здесь первые r ограничений имеют вид неравенств со знаком меньше либо равно

затем идет группа неравенств со знаком больше либо равно

и, наконец, группа ограничений со знаком = .

Для приведения задачи к канонической форме, где все ограничения имеют видравенств, вводят дополнительные переменные   , которые тоже считаются неотрицательными и записывают исходную задачу в виде

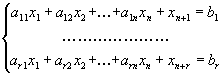
(1.17)

 ,

т.е. в неравенстве со знаком меньше либо равно добавляют дополнительную неотрицательную переменную, а из неравенства со знаком больше либо равно вычитают дополнительную переменную.

В целевую функцию эти дополнительные переменные включают с коэффициентом 0, т.е. фактически они в целевой функции отсутствуют.

Получив решение задачи (1.17), т.е. решение задачи в канонической форме, для получения решения исходной задачи (1.16) надо просто выбросить из решения значения введенных дополнительных переменных.

Пример

Привести к каноническому виду задачу

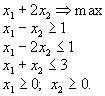
Введем дополнительные переменные   . Переводя max в min, запишем задачу в виде

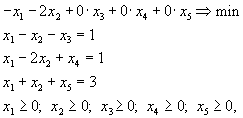
что и дает эквивалентную задачу в канонической форме.

Билет 3. Существование Оптимального Решения Задачи Линейного Программирования

Теорема о существовании оптимального базисного решения задачи линейного программирования. Критерий оптимальности

Определение 1.   Задача математического программирования:

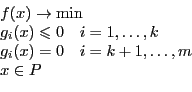
Пусть

Полагаем, что  . Пусть  . Если  --решение, то  , но решение не всегда существует.

Определение 2.     называется вектором Куна--Таккера, если верно

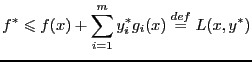 (регулярная функция Лагранжа)

Теорема 1.   Пусть   -- выпуклое   -- выпуклые на  ,   -- линейные. Пусть хоть одно из следующих двух условий выполнено:

1. .

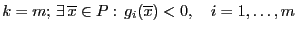2.  -- полиэдр,   -- линейны,  .

Тогда существует вектор Куна--Таккера.

Определение 3.   Двойственной называется задача следующего вида:

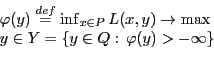
Теорема 2.   Пусть существует вектор Куна--Таккера и  . Если  , то   и множество решений   и совпадает с множеством векторов Куна--Таккера.

Определение 4.   Общая задача линейного программирования:

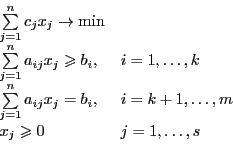
Пусть  ,  ,

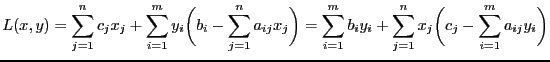
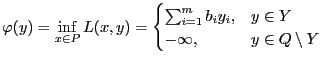
Получили двойственную задачу:

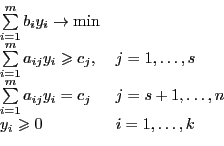
Теорема 3.   Двойственная к двойственной совпадает с исходной.

Теорема 4. (критерий разрешимости задачи ЛП)   Пусть   и целевая функция ограничена снизу на допустимом множестве (  ). Тогда задача ЛП имеет решение.

Доказательство. По теореме 2. существует решение двойственной задачи. А по теореме 3. существует решение прямой задачи. 

Определение 5.    -- выпуклое множество,   называется угловой точкой этого множества, если представление этой точки в следующем виде   возможно только в одном случае:  .

Поставим задачу ЛП в канонической форме:

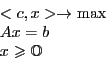
Очевидно, что допустимое множество   выпуклое. Будем считать, что  . Мы можем выбрать  ЛНЗ, а все остальные столбцы будем обозначать  . Обозначим

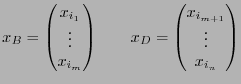
Определение 6.   Переменные в   называются базисными, а в   -- не базисными.

Определение 7.   Решение системы   называется базисным, если  , т.е.  .

Определение 8.   Базисом базисного решения называется совокупность столбцов  , входящих в  .

Определение 9.   Базисное решение называется допустимым, если  .

Определение 10.   Допустимое базисное решение называется невырожденным, если значения базисных переменных  , иначе оно вырождено.

Определение 11.     называют допустимым базисным решением, если столбцы матрицы  , соответствующие ненулевым координатам вектора  , линейно независимы.

Базис однозначно определяет допустимое базисное решение, обратное неверно.

Теорема 5.   Если  , то существует допустимое базисное решение.

Теорема 6.   Любое допустимое базисное решение является угловой точкой множества   и наоборот.

Симплекс метод представляет собой вычислительную процедуру, осуществляющую перебор допустимых базисных решений задачи до нахождения оптимального допустимого решения. При этом на каждой итерации симплекс метода в зависимости от значений некоторых параметров делается один из трех следующих выводов:

1. рассматриваемое ДБР является решением задачи;

2. целевая функция неограниченно возрастает;

3. осуществляется переход к новому допустимому базисному решению с нехудшим значением целевой функции.

Описание одной итерации симплекс метода. Пусть известно некоторое ДБР.  .   образуют базис точки  . Будем рассматривать матрицу   базисных столбцов и соответствующие  , введенные по аналогии.

    т.к. 

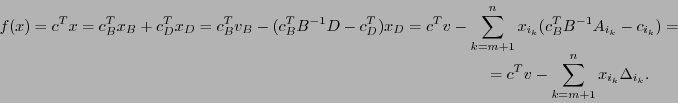
Для   имеем  .

Задача переписывается в следующем виде:

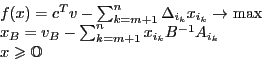
Пусть  .

Всю информацию о коэффициентах принято записывать в виде симплекс таблицы.

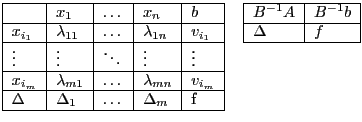
Как меняются переменные? Рассмотрим  . . Мы хотим выбрать номер небазисной переменной   и ее значение   так, чтобы точки, получающиеся по этим формулам, удовлетворяли всем ограничениям задачи и при этом . Возможны три случая:

1)  . Покажем, что в этом случае точка   -- решение. Рассмотрим  .

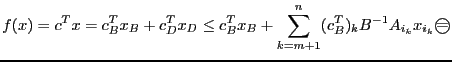
Это неравенство следует из неотрицательности  .

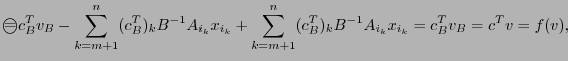
т.е.   -- решение.

2)  . Тогда задача не имеет решения.

Рассмотрим  .   (т.к. мы пользовались формулами перехода), т.е.  .  .

3)  . Можем перейти к новому ДБР с нехудшим значением целевой функции.

Пусть   достигается на  . Построим новую точку   по формулам пересчета. .  .  .

Теорема 7.   Точка   является допустимым базисным решением, базисом будут столбцы   и  .

Билет 4. Графическое решение задач линейного программирования . Алгоритм.