
- •Введение
- •1. Основные понятия и определения.
- •1.1. Алгоритм.
- •1.2. Этапы программирования.
- •2. Язык программирования Quick Basic
- •2.1. Среда Qвasic
- •2.2. Имена
- •Dim_имя массива (размерность)[,имя массива (размерность)…]
- •2.3.3. Некоторые директивы языка.
- •2.3.4. Выражения
- •2.3.5. Функции
- •3. Операторы.
- •3.1. Оператор присваивания.
- •3.2. Операторы управления.
- •Goto_номер строки
- •If_выражение - условие _then_группа операторов [_else_группа операторов]
- •If логическое выражение then группа операторов 1
- •1 Вариант: 2 вариант:
- •3.2.3. Оператор множественного выбора
- •3.3. Операторы цикла.
- •3.4. Прекращение выполнения и завершение программы
- •3.5. Подпрограммы
- •Gosub_номер строки
- •3.6. Организация ввода.
- •Input [;][«подсказка»;]переменная[,переменная]
- •Data_ константа [,константа]… read_ переменная [,переменная]…
- •Randomize_база
- •3.7. Организация вывода.
- •Print_[выражение[,выражение]]…[;]
- •Print_using шаблон [_шаблон]…; выражение [,выражение]…[;]
- •3.8. Графика языка.
- •3.9. Работа с файлами.
- •Input_#номер файла[,переменная][,переменная]
- •Eof(номер файла)
- •4. Базовые алгоритмы.
- •5. Советы по выполнению задания.
- •Примеры решения задач.
- •6.1. Задачи на вычисление функций и сумм.
- •1. Вычислить функцию:
- •Задачи с использованием массивов.
- •6.2.1. Задание и распечатка массивов.
- •1. Элементы массива задаются с клавиатуры:
- •3. Элементы массива вводятся из блока data:
- •4. Элементы массива задаются случайными числами:
- •5. Элементы двухмерного массива ( матрицы ) задаются случайными числами:
- •6.2.2. Операции над элементами массивов.
- •Найти положительные элементы. Организовать из найденных элементов отдельный массив:
- •Найти элементы, кратные 3. Организовать из найденных элементов отдельный массив:
- •Найти максимальный элемент в каждой
- •Найти максимальный элемент в главной диагонали матрицы и его порядковый номер:
- •6.3. Задачи на приближенное вычисление площади фигур, объемов.
- •6.4. Задачи с использованием метода итераций.
- •6.4.1. Решение систем уравнений.
- •6.4.2. Вычисление корней уравнений.
- •6.5. Вычислить значения определенных интегралов.
- •Приложение 1 Список ошибок периода выполнения программы
- •Приложение 2 Список зарезервированных слов
- •Содержание
- •1. Основные понятия и определения.
- •1.1. Алгоритм.
- •Список литературы
6.4. Задачи с использованием метода итераций.
6.4.1. Решение систем уравнений.
Вычислить корни уравнений
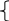
![]() на отрезке [ 0; 1 ]
с точностью
на отрезке [ 0; 1 ]
с точностью
![]()
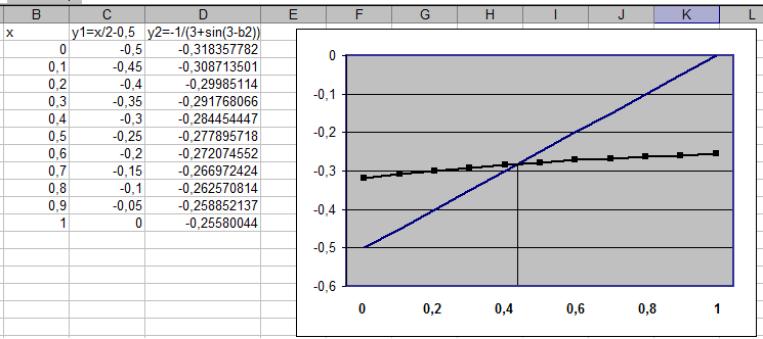
Для определения корней уравнений можно использовать метод итераций. Для этого следует преобразовать уравнения в форму X=f(X):
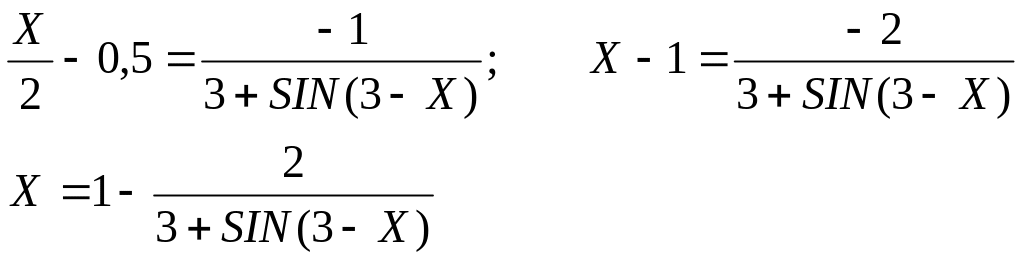
X0 = 0: E = .1: K = 0
10 : X = 1 - 2 / (3 + SIN(3 - X0))
IF ABS(X - X0) <= E THEN GOTO 20
X0 = X: K = K + 1
IF K > 6 THEN GOTO 20
GOTO 10
20 : PRINT USING" X=#.##"; X
ОТВЕТ: X=0.43
6.4.2. Вычисление корней уравнений.
1.
![]() на отрезке
[ 0 ; 1 ] с точностью
на отрезке
[ 0 ; 1 ] с точностью
![]() .
.
CLS
x0 = 0: E = .001
10 : Y = .2 + (COS(x0)) ^ 2 - 1 / (1 - x0 ^ 3) ^ .5
IF Y < E THEN GOTO 20
x0 = x0 + E
IF x0 > 1 THEN GOTO 20
GOTO 10
20 : PRINT " X=";: PRINT USING "##.###"; x0
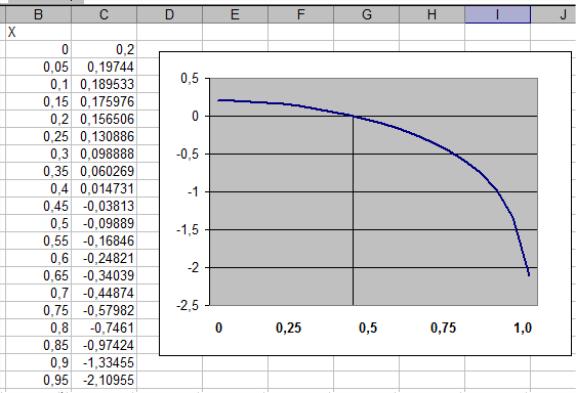
ОТВЕТ: X= 0.414
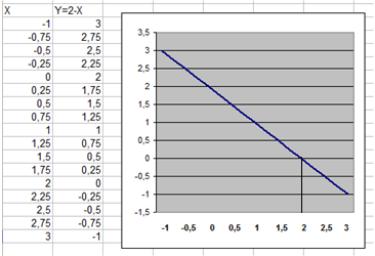
2. Y=2-X на отрезке [ 1 ; 2,5 ] с точностью
CLS
X0 = 1: XK=2.5: E = .001
10: Y = 2 - X0
IF Y < E THEN GOTO 20
X0 = X0 + E
IF X0 > XK THEN GOTO 20
GOTO 10
20: PRINT " X=";
PRINT USING”##.###”;X0
ОТВЕТ: X= 1.999
6.5. Вычислить значения определенных интегралов.
1.
Подынтегральная функция
![]() =
=![]() ,
метод прямоугольников с числом отрезков
50 на интервале интегрирования [ 0 ; 2].
,
метод прямоугольников с числом отрезков
50 на интервале интегрирования [ 0 ; 2].
X = 0: S = 0
DX = 2 / 50
FOR I = 1 TO 51
Y = (X ^ 4 - 4) / (X + 2) ^ 2
DS = Y * DX: S = S + DS: X = X + DX
IF X >= 2 THEN GOTO 10
NEXT I
10 : PRINT " S=";
S= -.5189601
2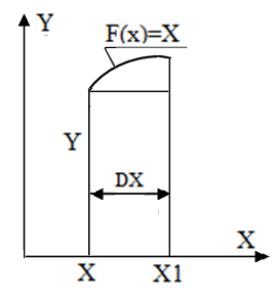 .
Подынтегральная функция
=
,
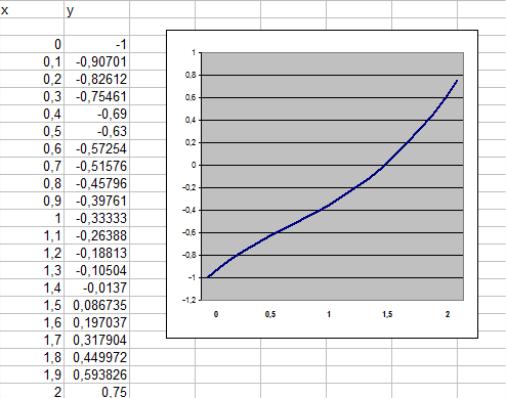
метод прямоугольников (по левому краю)
с числом отрезков 50 на интервале
интегрирования [ 0 ; 2].
.
Подынтегральная функция
=
,
метод прямоугольников (по левому краю)
с числом отрезков 50 на интервале
интегрирования [ 0 ; 2].
X = 0: S = 0: DX = 2 / 50
FOR I = 1 TO 50
Y = X: DS = Y * DX
S = S + DS: X = X + DX
IF X >= 2 THEN GOTO 10
NEXT I
10: PRINT " S="; S
ОТВЕТ: S= 196

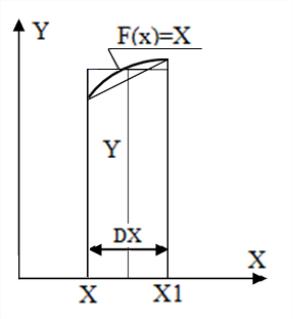
3. Подынтегральная функция = , метод прямоугольников (по середине отрезка) с числом отрезков 50 на интервале интегрирования [ 0 ; 2].
X = 0: S = 0
 DX = 2 / 50
DX = 2 / 50
FOR I = 1 TO 50
X1 = X + DX
Y = (X + X1) / 2
DS = Y * DX
S = S + DS
X = X + DX
IF X >= 2 THEN GOTO 10
NEXT I
10: PRINT " S="; S
ОТВЕТ: S=2

4. Подынтегральная функция = , метод трапеций с числом отрезков 50 на интервале интегрирования [ 0 ; 2].
X = 0: S = 0
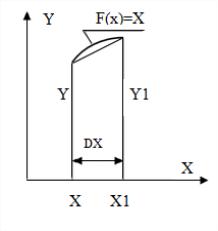 DX = 2 / 50
DX = 2 / 50
FOR I = 1 TO 50
X1 = X + DX
Y = X: Y1 = X1
DS = (Y + Y1) / 2 * DX
S = S + DS
X = X + DX
IF X >= 2 THEN GOTO 10
NEXT I
10: PRINT " S="; S
ОТВЕТ: S= 2
