№1).Системы линейных уравнений (основные понятия).

Линейным уравнением с неизвестными на множество R называется уравнение вида . Если b=0, то линейное уравнение называется однородным. Если то система называется неоднородной. Сист назыв совместной или разрешимой если имеет хотя бы 1 решение. Совместная система назыв определ если она имеет только 1 решение, и неопредел если имеет более 1 решения. 2 СЛУ с 1 и тем же числом неизвестных называются эквивалентными если множ их решений совпадают, если каждое решение первой из них является решением 2-ой.

Теорема 1.  При элементарных преобразованиях системы линейных уравнений получаем систему, равносильную первоначальной.

Доказательство.  Пусть дана система линейных уравнений

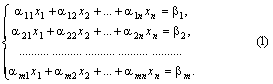
Рассмотрим лишь преобразование 3 (для остальных преобразований утверждение очевидно). Прибавим ко второму уравнению системы первое уравнение, умноженное на число  :

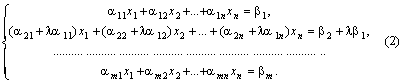
Докажем, что системы линейных уравнений (1) и (2) равносильны.  Пусть арифметический вектор   является решением системы (1). Это значит, что при подстановке в (1) вместо переменных  соответствующих значений получаем систему верных числовых равенств

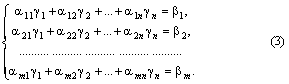
Прибавим ко второму равенству первое, умноженное на число  :

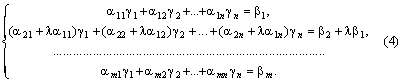
Полученная система равенств (4) означает, что арифметический вектор  является решением системы (2).

Для доказательства обратного заметим, что равенства (3) получаются из равенств (4), если ко второму равенству из (4) прибавить первое, умноженное на 

№2).Метод последовательного исключения неизвестных.

Всякую матрицу путем элементарных преобразований можно привести к ступ. Виду. док-во: Если данная матрица нулевая, то она ступеньчетая. Если не нулевая, то пусть ϒ1 – номер 1го не нулевого столбца. Переставим, если нужно строки а1 ϒ1≠ после этого прибавим к строке, начиная со 2й, 1ю строку умноженное на подходящее число с тем расчетом, чтобы все элементы ϒ1 столбца= 0 со 2й строки.

№3).Арифметические n-мерные векторы, действия над ними.

n-мерным вектором - называется упорядоченная система из n чисел.

Вектор 0= (0,0,…,0), все координаты которого ровны 0, назыв нулевым вектором.

Вектор назыв противоположным вектору

Суммой двух векторов и назыв вектор, координаты которого равны сумме соответствующих координат.

Св-ва сложения векторов. 1). свойство коммутативности сложения векторов a + b = b + a; 2). свойство ассоциативности векторов (a + b) + c = a + (b + c); 3). существует нейтральный вектор по операции сложения, им является нулевой вектор, a + 0 = a; 4). для любого вектора существует противоположный вектор, которые в сумме дают нулевой вектор a + (-a) = 0; 5). существует нейтральное число по операции умножения, им является единица 1*а=а. Св-ва умножения векторов. 1).1*a=a 2). (AB)c=A(Bc) 3). (A+B)c=Ac+Bc 4). A(BC)=AB+AC.

№4).Линейная зависимость, базис и ранг системы арифметических n-мерных векторов.

Система векторов (1) где назыв линейно зависимой если хотя бы 1 из векторов этой системы является линейной комбинацией других векторов системы (1).

Рангом сист векторов назыв число векторов в базисе этой системы.

Св-ва линейной зависимости. 1).Если к линейно зависимой системе векторов   добавить несколько векторов, то полученная система будет линейно зависимой. Доказательство. Так как система векторов   линейно зависима, то равенство   возможно при наличии хотя бы одного ненулевого числа из чисел  . Пусть  .

Добавим к исходной системе векторов еще s векторов  , при этом получим систему  . Так как   и  , то линейная комбинация векторов этой системы вида   представляет собой нулевой вектор, а  . Следовательно, полученная система векторов является линейно зависимой. 2).Если из линейно независимой системы векторов   исключить несколько векторов, то полученная система будет линейно независимой. Доказательство. Предположим, что полученная система линейно зависима. Добавив к этой системе векторов все отброшенные векторы, мы получим исходную систему векторов. По условию – она линейно независима, а в силу предыдущего свойства линейной зависимости она должна быть линейно зависимой. Мы пришли к противоречию, следовательно, наше предположение неверно. 3).Если в системе векторов   есть хотя бы один нулевой вектор, то такая система линейно зависимая. Доказательство. Пусть вектор   в этой системе векторов является нулевым. Предположим, что исходная система векторов линейно независима. Тогда векторное равенство   возможно только тогда, когда  . Однако, если взять любое  , отличное от нуля, то равенство   все равно будет справедливо, так как  . Следовательно, наше предположение неверно, и исходная система векторов линейно зависима. 4).Если система векторов   линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов   линейно независима, то ни один из векторов не выражается через остальные.

Доказательство. Сначала докажем первое утверждение.

Пусть система векторов   линейно зависима, тогда существует хотя бы одно отличное от нуля число   и при этом верно равенство  . Это равенство можно разрешить относительно  , так как  , при этом имеем 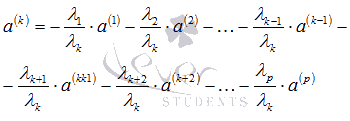Следовательно, вектор   линейно выражается через остальные векторы системы  , что и требовалось доказать.

Теперь докажем второе утверждение.

Так как система векторов   линейно независима, то равенство   возможно лишь при  .

Предположим, что какой-нибудь вектор системы   выражается линейно через остальные. Пусть этим вектором является  , тогда  . Это равенство можно переписать как  , в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором   отличен от нуля, что указывает на линейную зависимость исходной системы векторов. Так мы пришли к противоречию, значит, свойство доказано.

№5).Элементарные преобразования матриц. Ступенчатая матрица.

1). Прибавление к 1 строке другой умноженной на чило.

2). Перестановка 2-х строк.

3). Умножение 1-ой строки умноженной на число отличное от нуля.

Матрица назыв ступенчатой если:

1). Номера ведущих элементов ее не 0 строк образуют строго возрастающую последовательность.

2). 0 строки если они стоят в конце.

Теорема. Всякую матрицу путем элементарных преобразований можно привести к ступенчатому виду. Доказательство.  Пусть дана система линейных уравнений

 Предположим сначала, что в первом уравнении системы первый коэффициент  . Тогда легко исключить   из остальных уравнений. Умножив первое уравнение на   и прибавив ко второму уравнению, исключим   из второго уравнения. В итоге получим систему линейных уравнений вида

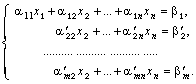
Теперь можно заняться подсистемой ниже первого уравнения.

Если же  , но существует уравнение, в котором коэффициент при   отличен от нуля, то можно это уравнение поставить на первое место, а можно это уравнение прибавить к первому уравнению, выполняя тем самым главное элементарное преобразование. В любом случае придем к рассмотренному случаю.

Если же все коэффициенты при переменной   равны нулю, то перейдем к рассмотрению системы линейных уравнений относительно переменных  . Наконец, заметим, что если в системе (1) все коэффициенты при переменных равны нулю, то система (1) в соответствии с определением 10 является ступенчатой.                                        

№6).Ранг матрицы. Теорема о ранге ступенчатой матрицы. Вычисление ранга матрицы.

Рангом матрицы А называется максимальное число ее линейно независимых строк или столбцов. Ранг ступенчатой матрицы равен числу ее не нулевых строк.

Теорема. Ранг матрицы не меняется при элементарных преобразованиях.

  Для доказательства теоремы достаточно убедиться в том, что в результате элементарных преобразований нулевой определитель остается нулевым, а ненулевой – ненулевым. 

1).Перестановка строк или столбцов матрицы изменяет только знак определителя.

2).При умножении строки (столбца) матрицы на ненулевое число определитель умножается на это число.

3).Определитель не изменяется, если к строке (столбцу) прибавляется другая строка (столбец).

Для того чтобы найти ранг матрицы элементарным способом достаточно привести ее с помощью элементарных преобразований к ступенчатому виду, число строк отличных от 0 и будет ровняться рангу матрицы.

Теорема. Ранг по строкам матрицы А равен рангу по столбцам. Док-во. Предположим что ранг по строкам матрицы А=m а ранг по столбцам равен n.Максимально линейно не зависимые первые n-строк и 1ые м-столбцов. Обознавим через В- матрицу стоящее на персечении базисных строк и базисных столбцов.

В=а11 а12..а1n а21 а22..а2n

Ам1 ам2..амn В1’=a11 a21..an1 b2’=a12 a22..an2 Bm’=a1n a2n..ann Т.к в В векторы н-мерные, то ранг (в..в2..вн) =м ≤н, в силу указанного ранее свойства линейно зависимых систем векторов , ранг в1’=н≤м из м-мерных векторов. Т.к м ≤н, н≤м следует, что м=н.

№7).Критерии совместимости СЛУ.

Теорема. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.

Док-во. Пусть сист 1 совместна, это значит что уравнение 2 имеет решение и пусть удовлетворяющий уравнению 2, т.е. , это значит что , имеют одинаковые ранги, т.е. ранг а =рангу b, где а-основная, а b-раздельная матрица сист 1. Пусть теперь ранг а=b, это возможно тогда, когда следовательно является решением уровнения 2, а тем самым и сист 1 т.е. СЛУ совместна. Если ранг=числу неизв., то сист. Имеет единственное решение. Если ранг меньше числа неизвестных, то имеет множество решений. Если ранг основной матрицы не равен рангу расширенной матрицы, то сист. Решений не имеет.Добавление столбца из нулей не может повысить ранга матрица.

8).Свойства СЛОУ.

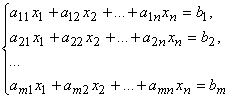
Такая система всегда совместна т.к. имеет 0 решение .

Если она определена то она имеет только 1 нулевое решение. Если неопределенна то имеет хотя бы 1 не нулевое решение(и даже бесконечно много таких решений).

Если х=[а1а2..ан] является решением системы, то для любого К из множества R, кх=[ка1 ка2..кан] является решением.

2) Пусть х=а1 а2..ан, у=в1 в2..вн, является решением системы, тогда х+у является решением. 3) любая лин. Комбинация решение ОСЛУ является решением этой сист..Док-во: пусть х1х2..хр являются произвольным набором решений х1, составим лин. Комбинации: к1х1 +к2х2+крхр. Каждый из векторов к1х1, к2х2..крхр, является решением, а всилу св.2, сумма этих решений является решением системы. Пусть система обладает не нулевым решением, Т≠{0}, следвотельно во мн.Т,суествует базис а1а2..ар, хТ, и линейно выражается через векторы базиса. Х=µ1а1+ µ2а2.. + µрар, с другой стороны в силу предыдуего выше утверждения, а1а2арТ, следовательно µ1а1+ µ2а2+..+ µрар€Т, таким образом множество решений ОСЛУ состоит из: µ1а1+ µ2а2+..+ µрар, выржаение Х=µ1а1+ µ2а2.. + µрар охватывает все выражения системы.

9).Фундаментальная система решений СЛОУ.

10).Св-ва решений СЛНУ.

Понятие ассоцированых систем: Если у 2х систем коэф. При неизвестных одинаковые, но одна система однородная, а друга не однородная, то эти системы назыв. Ассоц. Однородная называют приведенной системой неоднородная. св-ва: 1)сумма любого решения неоднородной с любым решение приведенной является решением неоднородной.2) Разность любых 2х решений неоднородной есть решение однородной. Теорема(7)

11).Перестановки. Теорема о транспозиции.

Всякое расположение чисел в определенном порядке называется перестановкой из n-символов, или из m-чисел.

Теорема: Всякая транспозиция меняет четность перестановки на противоположную.

Док-во. рассмотрим случай когда транспонируемые символы I и j стоят рядом, т.е. перестановка имеет вид …ij…, где … обозначаются символы не затрагивающие транспозиции, транспозиция преобразует нашу перестановку в …ji…, понятно что в каждой из перестановок символы ij составляют одни и те же инверсии с символами оставим на месте. Если символы ij между собой инверсии не составляют, то в новой перестановке появится 1 новая инверсия, т.е. число инверсий увеличится на 1, если ij составляют инверсию, то во второй перестановке она пропадет, т.е. число инверсий на 1 уменьшится, в обоих случаях четность перестановки меняется. Пусть теперь между транспозициями i и j расположено s символов (1), транспонируемые символы i и j можно получить в результате последующего выполнения 2s+1 транспозиции соседних элементов, а именно

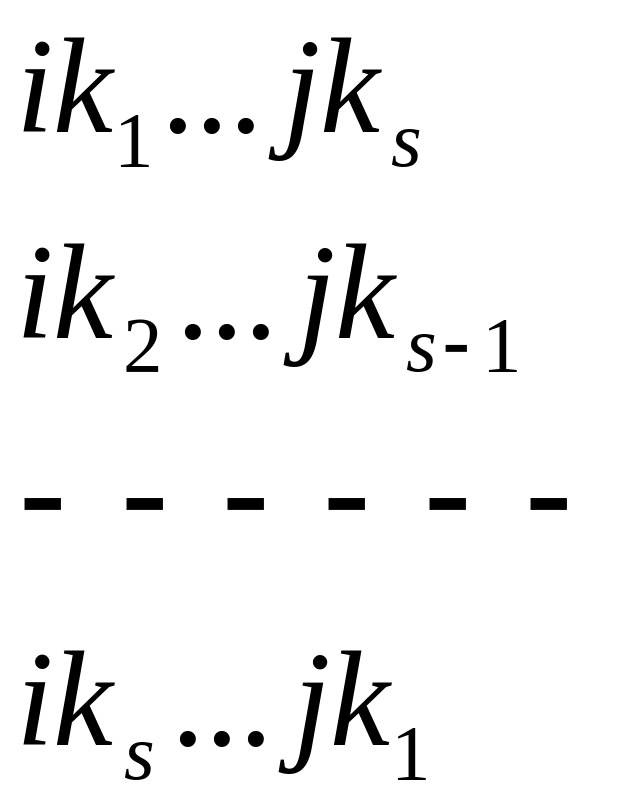
Таким образом мы нечетное число раз поменяли четность перестановки и поэтому перестановка (2), (1) и (2) имеет противоположную четность.

12).Подстановки. Четность подстановки.

13).Группа подстановок.

14).Определитель квадратной матрицы n-го порядка. Вычисление определителей 2-го и 3-го порядка.

15).Св-ва определителей квадратной матрицы n-го порядка.

1). ОП не меняется при транспонировании.

2). Если хотя бы один ряд (строка или столбец) состоит из нулей, то определитель равен нулю. 

Док-во: пусть все строки j=0 тогда в каждый член ОП войдет множитель с нулем.

3). Если в определителе поменять местами два соседних параллельных ряда (строки или столбцы), то определитель поменяет знак на противоположный.

4). Если ОП содержит 2 одинаковые строки, то он равен 0.

5). Общий множитель ОП можно вынести за знак ОП

6). ОП содержащий 2 пропорциональные строки =0

7). ОП не меняется если к элем 1-ой из его строк прибавляется соответствующий элем другой строки умноженный на одно и тоже число.

8).Если 1 из строк ОП есть линейная комбинация его других строк то ОП=0.

Докажем 1 свойство: a1j1 a2j2 anjn.(3) Все множетили (3) входят в определительСАМЫЙ БЛЯДЬ ОБЫЧНЫЙ СУКА ННОГО ПОРЯДКА ЖИ ЕСТЬ.тк стоят в разных строках и столбцах т.е (3) служит членом для определителя, знак члена (3) определяется четностью подстановки 12..n

j1j2jn

, определитель- 1ые индексы опреелителя указывают номера столбцов и члену (3) соотв. Подстановка j1j2jn

1 2.n

Различные но имеют одинаковую четность, член (3) имеет в обоих определителях один и тот же знак. Всякое утверждение о строках определителя справедливо для его столбцов.

16).Минор и АД элемента определителя. Теорема о произведении .

Минором ОП ∆ n-го порядка, называется ОП, который получается из ∆ вычеркнув

I строку и J столбец.

АД называется минор этого ОП, взятый со знаком *

Теорема. Каждый член произведения элемента ОП на его АД является член ОП и при том с тем же знаком что и в произведении . Док-во.

17).Разложение определителя по элементам строки или столбца. Вычисление определителя n-го порядка.

Теорема о разложении определителя по элементам строки. Определитель матрицы  A  равен сумме произведений элементов строки на их алгебраические дополнения: Док-во:

18).Правило Крамера.

Теорема: если в сист. ЛУ число уравнений = числу неизвестных и ОП отличен от 0, то эта сист имеет 1 решение и находится по формулам. … .

19).Матрицы однотипные, равные, квадратные. Нулевая матрица. Сложение матриц и его св-ва.

Матрицы назыв. Однотипными - если они имеют одинаковое число строк и столбцов.

Если число строк = числу столбцов, то матрица называется квадратной.

Матрицы называются равными если у них одинаковое число строк и столбцов, и все соответствующие элементы совпадают.

Матрица все элементы которой = 0 называется нулевой матрицей.

Слаживать можно только однотипные матрицы. Св-ва; 1). A+B=B+A.

2). (A+B)C=A+(B+C). 3). A+0=A. 4). ∀A∃(-A) A+(-A)=0.

Однотипные матрицы образуют Абелеву группу.