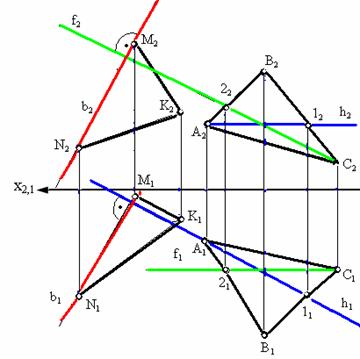
- •22) Следы прямой
- •23) Построение следов плоскости.
- •24) Нахождение точки пересечения прямой с плоскостью.
- •25. Построение линии пресечения двух плоскостей.
- •26. Построение линии пересечения поверхности цилиндра плоскостью
- •27. Построение линии пресечения двух поверхностей методом секущих плоскостей.
- •29. Параллельность прямой и плоскости.
- •30. Перпендикулярность прямой и плоскости.
- •31. Параллельность плоскостей.
- •32. Перпендикулярность плоскостей.
- •33)Определение видимости при пересечении двух плоскостей общего положения
29. Параллельность прямой и плоскости.

30. Перпендикулярность прямой и плоскости.
Из школьного курса геометрии известно что прямая перпендикулярна плоскости если она перпендикулярна двум пересекающимся прямым этой плоскости.
Для задания прямой перпендикулярной плоскости в качестве пересекающихся прямых удобно выбрать линии уровня – фронталь и горизонталь. В этом случае можно воспользоваться свойствами проекций прямого угла.
Признак перпендикулярности прямой и плоскости можно сформулировать в виде теоремы.
Теорема:
Для того, чтобы прямая m была перпендикулярна плоскости s, необходимо и достаточно, чтобы горизонтальная проекция прямой m1 была горизонтальной проекции горизонтали (m1 h1), а фронтальная проекция прямой m2 – фронтальной проекции фронтали (m2 f2).
Задача 1. Построить ортогональные проекции перпендикуляра m, опущенного из точки D на плоскость s (ABC).
Решение:
1. На ортогональном чертеже строим в плоскости s (ABC) проекции фронтали f (f1, f2) и горизонтали h (h1, h2).
2. Проводим m1 h1 причем D1 m1.
3. Проводим m2 f2 причем D2 m2.
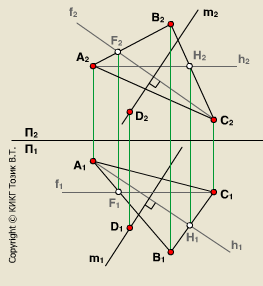
Прямая m (m1, m2) – искомый перпендикуляр, так как она перпендикулярна двум пересекающимся прямым плоскости s (ABC) = h f.
Задача 2. Построить плоскость s, проходящую через точку K и перпендикулярную прямой m общего положения.
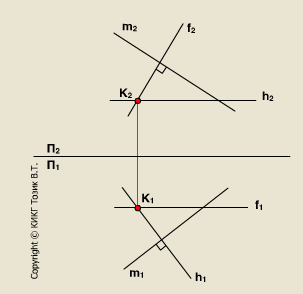
Решение:
Если прямая m общего положения, то искомая плоскость также общего положения. Эту плоскость зададим двумя пересекающимися прямыми, перпендикулярными прямой m. Такими прямыми будут фронталь f и горизонталь h.
Алгоритм построения:
1. f2 m2, K2 f2
2. f1 K2K1, K1 f1
3. h2 K2K1, K2 h2
4. h1 m1, K1 h1
5. Плоскость s = h f - искомая плоскость.
31. Параллельность плоскостей.
Определение: еcли две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.
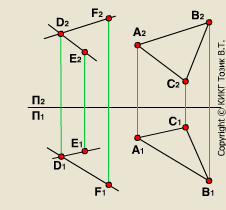
Рассмотрим пример. Пусть нам дана плоскость a, заданная треугольником АВС и произвольная точка D. Требуется через точку D провести плоскость b параллельную a (АВС). Для того чтобы через точку D провести плоскость параллельную плоскости a (АВС), достаточно построить две пересекающиеся прямые, параллельные двум пересекающимся прямым плоскости a, так чтобы точка D принадлежала этим прямым. Например, проведём прямую DE || AC, на чертеже D1E1 || А1С1 и D2E2 || А2С2 и прямую DF || AB, на чертеже D1F1 || А1B1 и D2F2 || А2B2. Две пересекающиеся прямые DE и DF определяют плоскость b. Плоскость b || a, так как две пересекающиеся прямые DE и DF, принадлежащие плоскости b, параллельны двум пересекающимся прямым АВ и АС, принадлежащим плоскости a.
32. Перпендикулярность плоскостей.
Плоскости α и β перпендикулярны, если одна плоскость проходит через перпендикуляр другой плоскости.
На рис. 4.3 показана прямая а перпендикулярная плоскости α , (следовательно, любая плоскость, проходящая через прямую а, будет перпендикулярна плоскости α). На рис. 4.4 изображены две проецирующие плоскости β и γ и произвольная плоскость δ, следы которой проходят через следы прямой а.
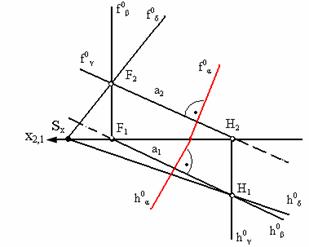
Рис. 4.4. Условие перпендикулярности плоскостей
На рис. 4.5 изображена прямая b, перпендикулярная плоскости Δ АВС, следовательно, любая плоскость, проходящая через прямую b, будет перпендикулярна плоскости Δ АВС.