Вопрос № 38: Частные производные:

1. Частные производные.

   1. Геометрическая интерпретация при п=2.

Дифференцирование функции многих переменных:

Для всех задана скалярная функция , или скалярное поле.

При п=2 определена в пространстве некоторая поверхность.

Понятие частных дифференциалов:

определена в окрестности точки Придадим приращение х, тогда функция получит частное приращение:

Определение: Придел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю – если он существует – называется частной производной функции по переменной х в точке и обозначается:

Из определения следует, что отыскание частных производных – есть дифференцирование функции , как функции одной переменной. По этом правила дифференцирования, а также таблица производных сохраняется.

Геометрический смысл частных производных:

– плоскость, параллельная горизонтальной плоскости.

, то есть значение – есть тангенс угла наклона касательной, проведенной к линии пересечения поверхности и плоскости , в точке, где .

Вопрос № 39: Дифференцируемость функции

1. Дифференцируемость функции .

2. Необходимые и достаточные условия дифференцируемости.

Рассмотрим , определённую в точке .

дифференцируема в , если её полное приращение представимо в виде

А,В,С – не зависят от приращений аргументов, а

Необходимые условия дифференцирования:

Пусть дифференцируема в точке :

0. непрерывна в .

1. Существуют частные производные по всем переменным.

Доказательство:

0. Из ( ) следует: при приращениях всех переменных, стремящихся к нулю, величина приращения функции тоже стремится к нулю.

1. Докажем, что частная производная по х равна А: Возьмём все приращения, кроме приращения по х, равными нулю, тогда: при получим: Аналогично доказываются и остальные частные производные.

Достаточные условия дифференцирования:

Если имеет в точке непрерывные частные производные, то полное приращение будет представлено в виде:

Вопрос № 40: Производная по направлению:

1. Производная по направлению.

2. Градиент скалярного поля.

3. Связь с производной по направлению.

Если функция дифференцируема в точке , то существует производная по направлению .

Согласно Формуле вычисления скалярного произведения градиент запишется следующим образом:

1. Если

2. 

3. В направлении градиента

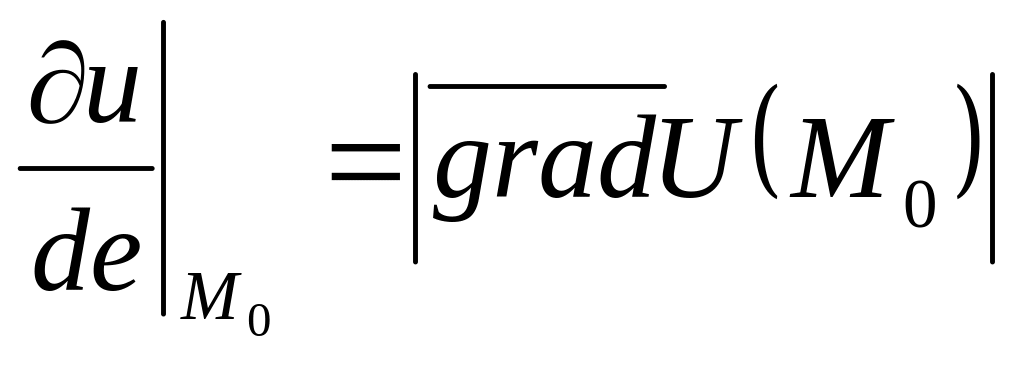
Пусть множество точек, где и точка принадлежат этому множеству. В окрестности точки М₀ существуют частные производные . Следовательно для всех в₀ больших нуля прямоугольный треугольник: . Существует пирамида: , пересекающая треугольник. ***

Вопрос № 41: Дифференциал f(M), M принадлежит Rⁿ:

1. Дифференциал f(M), M принадлежит Rⁿ.

2. Линеаризация функции.

3. Геометрический смысл дифференциала функции двух переменных.

Дифференциал функции:

Дифференциалом функции является главное линейное отношение приращений переменных, как часть полного приращения дифференцированной функции, то есть .

Формула для вычисления дифференциала: .

При п=2, то есть

Производные второго порядка для функций п-переменных:

Производной второго порядка функции п-переменных называется производная от производной п-1-ого порядка по каждой из переменных.

Линеаризация функции:

При малы приращениях из следует, что

Геометрический смысл дифференциала функции двух переменных:

Дифференциал функции двух переменных – это приращение аппликаты касательной плоскости, при переходе от точки на касательной плоскости в точку .

Вопрос № 42: Производная сложной функции многих переменных:

1. Производная сложной функции многих переменных.

2. Полная производная.

Дифференцирование сложной функции:

1. Пусть , где , где множество значений принадлежит области определения функции, тогда: – сложная функция одной переменной t, тогда: если дифференцируемы в точке t, а дифференцируема, соответственно, в точке , то и дифференцируема по t, и существует дифференциал: – эта производная называется полной производной.

2. Пусть , где , пусть дифференцируемы в точке , а дифференцируема, соответственно, в точке , тогда функция дифференцируема как и существует дифференциал