Вопрос № 12 Предел функции:
Определение предела функции.
Функции одной переменно по Коши и по Гейне.
Функция
п-переменных:
Пусть каждой точке
по
некоторому закону ставится в соответствие
число “U”,
тогда говорят, что на
задана числовая функция
п-переменных:
Рассмотрим
точку
,
во всей её окрестности существуют точки
,
где
,
при этом
–
область определения функции.
Говорят, что число “b” –
,
если для всех
удовлетворяющих
условию
выполняется неравенство:
– По Коши.Говорят, что число “b” – , если для всех последующих точек
сходится в точке А,
соответствующая числовая последовательность
сходится к числу “b”
при к,
стремящимся к бесконечности. – По
Гейне.Число “b” называют
если для всех
удовлетворяющих условию
выполняется неравенство:
Для
построения
пусть
,
где
,
определена в некоторой окрестности
точки
,
за исключением, быть может, самой точки.
Вопрос № 13 Теоремы об арифметических действиях над функциями, имеющими конечный предел:
Определение предела функции по Гейне позволяет перенести все результаты, полученные для сходящихся последовательностей на функции, имеющие конечный предел. В частности справедливы теоремы об арифметических действиях:
Пусть
,
тогда:
Бесконечный предел:
–
говорят,
что функция имеет бесконечный предел,
если для всех
Вопрос
№ 14
Замечательный предел
:
:
Угол АОМ=х
МС перпендикулярно АО; МС есть синус х.
АВ – тангенс х
Из геометрических соображений MC< дуги АМ < AB
для
х
больших нуля.
Если
х
больше нуля, то –х
меньше нуля, и
Перейдём к пределу:
Согласно теореме о переходе в неравенство получим:
так
как
Вопрос № 15: Второй замечательный предел:
Можно
показать, что эта последовательность
является возрастающей и ограниченной
сверху, а значит имеет конечный придел.
,
аналогично для
Вопрос № 17: Непрерывность функции одной переменной в точке и на множестве:
Непрерывность функции одной переменной в точке и на множестве.
Свойства функций, непрерывных в точке.
Пусть
определена на
.
Рассмотрим
такое, что в любой её ε-окрестности
содержится точка
отличная от А.
непрерывна
в А,
если существует конечный предел
.
непрерывна на , если она непрерывна в каждой точке этого множества.
Рассмотрим
в А
полное приращение
,
тогда ясно, что для непрерывной функции
в А
необходимо и достаточно что бы
.
Свойства непрерывных функций:
Пусть
и
непрерывны в А, тогда
так же непрерывны в А.Пусть непрерывны в А и
,
тогда существует окрестность точки А,
в которой
и сохраняет свой знак
.
Доказательство:
;
возьмём ε>0 так, что
.
Для выбранного ε существует
такой,
что для всех точек М
условие
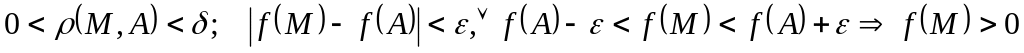в указанной окрестности точки А.
(О промежуточном значении) непрерывна на
,
и точки А
и В
принадлежат данному множеству, для
всех С,
где
на всей непрерывной прямой L,
соединяющей А
и В
существует М0
такое, что
.
При этом предполагается, что рассматривается
связное множество.Непрерывная на компакте1 функция ограничена на нём.
Непрерывная на компакте функция достигает на нём точной верхней и нижней грани, то есть существуют М1,2 из , такие, что
Непрерывная на компакте функция равномерно2 непрерывна на нём.