Схемы нерекурсивных фильтров

В общем случае линейным дискретным фильтром называется дискретная система, удовлетворяющая линейному разностному уравнению

                                                         (8.8),

где x(n) и y(n) – соответственно входная и выходная последовательности устройства.            Передаточная функция линейного дискретного фильтра имеет вид

( 8.9), который получается в результате применения z-преобразования к левой и правой частям уравнения (8.8).

            Значения выходной последовательности y(n) определяются N значениями входного дискретного сигнала x(n) в моменты nT, (n-1)T, (n-2)T, и т.д. и M-1 значениями самого выходного дискретного сигнала в прошлые моменты (n-1)T, (n-2)T и т.д.

            Фильтры, описываемые уравнением (8.8) называются рекурсивными.

            В частном случае, при   из (8.8) получаем

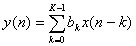                                                                                       (8.10).

В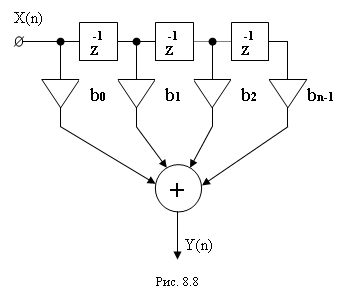 этом случае значение выходного дискретного сигнала y(n) в любой момент nT определяется лишь значениями входного дискретного сигнала в этот же момент и N-1 его прошлыми значениями. Фильтры, описываемые уравнением (8.10) называются нерекурсивными. Передаточная функция нерекурсивного фильтра имеет вид

                                                                                           

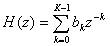
Прямая форма структурной схемы нерекурсивного фильтра является непосредственной реализацией передаточной функции нерекурсивного фильтра (8.11) или его разностного уравнения (8.10). Прячмая форма, представленная на рис.8.8 содержит N-1 элементов задержки, N умножителей и сумматор на N входов.

Каскадная (последовательная) форма структурной схемы нерекурсивного фильтра соответствует представлению передаточной функции (8.11) в виде произведения

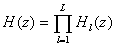                                                                                         (8.21),

где        или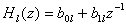   

Такое разложение всегда можно получить разложением H(z) на сомножители первого и второго порядка, каждый из которых реализуется с помощью упрощенной структуры биквадратного блока, а все составляющие блоки соединяются между собой последовательно.

8 .Связь между передаточной функцией и импульсной характеристикой. Реакция ф. На произв. Вход-е воздействие.

Импульсная характеристика

Импульсной характеристикой одномерного скалярного ЦФ называется его реакция на единичный импульс при нулевых начальных условиях.

Импульсная характеристика даёт полное описание линейной системы, из неё могут быть получены любые другие характеристики.

Зная импульсную характеристику , можно найти реакцию ЦФ (выходной сигнал ) на любое воздействие (входной сигнал ) при нулевых начальных условиях. Для этого следует воспользоваться формулой дискретной свёртки:

. (3.1)

Здесь верхний предел в суммах берётся равным текущему «дискретному времени» , а не бесконечности, что позволяет рассчитать переходный процесс в системе. Если представляет интерес установившийся режим, то верхний предел в суммах выражения (3.1) следует брать бесконечным.

Для физически реализуемых (физически возможных) систем выполняется следующее условие: при , которое означает, что реакция на выходе ЦФ не может появиться раньше воздействия на его входе (принцип временного детерминизма).

Матрица импульсных характеристик одномерного векторного стационарного линейного цифрового фильтра представляет собой квадратную матрицу размера , элементы которой являются реакциями на i-м выходе ЦФ при подаче на его l-й вход единичного импульса при нулевых начальных условиях и отсутствии сигналов на остальных входах [1, 2].

Для расчёта выходного сигнала одномерного векторного стационарного линейного ЦФ при произвольном входном сигнале и нулевых начальных условиях следует использовать векторно-матричный вариант формулы (3.1):

_//

Определение импульсной реакции на практике требуется, как правило, только для рекурсивных фильтров, так как импульсная реакция для НЦФ при известных значениях коэффициентов b(n), как это следует из выражения (2.2.1), специального определения не требует: h(n) ≡ b(n).

Если выражение для системы известно в общей форме (2.1.2), определение импульсной реакции производится подстановкой в уравнение системы импульса Кронекера с координатой k = 0 при нулевых начальных условиях. В соответствии с выражением (2.2.1) сигнал на выходе системы будет представлять собой импульсную реакцию системы.

Пример. Уравнение РЦФ: y_k = x_k + 0.5y_k-1.

Входной сигнал: x_k= d_o= {1,0,0,0,...}.

Расчет выходного сигнала при нулевых начальных условиях:

y_o = x_o+0.5 y_-1 = 1+0 = 1 = h_o.

y₁ = x₁+0.5 y_o = 0+0.5 = 0.5 = h₁.

y₂ = x₂+0.5 y₁ = 0+0.25 = 0.25 = h₂.

y₃ = x₃+0.5 y₂ = 0.125 = h₃. y₄ = x₄+0.5 y₃ = 0.0625 = h₄, и т.д.

Импульсный отклик фильтра: h_k = (O.5)^k, k = 0, 1, 2....

Определение импульсной реакции физической системы обычно производится подачей на вход системы ступенчатой функции Хевисайда, которая равна u(k)= 1 при k0, и u(k)= 0 при k<0: g(k) = h(n) u(k-n) = h(n). Отсюда: h(k) = g(k) - g(k-1).

Функция g(k) получила название переходной характеристики системы (из одного статического состояния в другое). Форму реакции фильтра на функцию Хевисайда можно видеть на рис. 2.1.4 (с точки k = 10 и далее) в сопоставлении с реакцией на импульс Кронекера в точке k=2.

_//

Передаточная функция

Передаточной функцией одномерного скалярного стационарного линейного ЦФ называется отношение Z-преобразования выходного сигнала к Z-преобразованию входного сигнала при нулевых начальных условиях:

. (3.3)

Нулевые начальные условия являются существенными в определениях импульсной характеристики h(n)и передаточной функции H(z) . Дело в том, что входной сигнал x(n) определяет вынужденную составляющую выходного сигнала y(n), а начальные условия — свободную (собственную) составляющую, поэтому при одном и том же входном сигнале x(n), но разных начальных условиях сигналы y(n) на выходе ЦФ в переходном режиме будут различными. В установившемся режиме поведение системы зависит только от входного сигнала x(n) и не зависит от начальных условий.

Передаточная функция H(z) и импульсная характеристика h(n) ЦФ связаны между собой парой Z-преобразований:

(3.4)

Если , то , ; - импульсное преобразование

,

Передаточная функция даёт полное описание стационарной линейной системы, из неё могут быть получены любые другие характеристики.

Зная передаточную функцию , можно при нулевых начальных условиях рассчитать реакцию ЦФ (выходной сигнал ) на любое воздействие (входной сигнал ). Алгоритм расчёта следующий:

(3.5)

Найдём выражение для передаточной функции одномерного скалярного стационарного рекурсивного линейного ЦФ. Для этого возьмём Z-преобразо-вание от обеих частей линейного разностного уравнения (2.2):

,

полагая входной сигнал при , а начальные условия в ЦФ нулевы-ми: . Воспользуемся теоремой линейности Z-преобразова-ния и теоремой запаздывания (см. § 1.3). В результате получим

. (3.6)

Отсюда, используя определение передаточной функции (3.3), находим

, (3.7)

где и — полиномы комплексного аргумента . Коэффициенты полиномов и являются вещественными числами для вещественного скалярного стационарного рекурсивного линейного ЦФ и комплексными числами для комплексного ЦФ.

Таким образом, передаточная функция одномерного скалярного стационарного рекурсивного линейного ЦФ является дробно-рациональной функцией комплексного аргумента , а параметры передаточной функции (3.7) равны коэффициентам и алгоритма линейной цифровой фильтрации (2.2).

Реакция на входное воздействие:

Можно оценить по разностному уравнению.

Выходной сигнал фильтра никогда не затухает.

Если , то ,

Реакция системы на единичный импульс – переходная ф-ция системы.

Фильтры с такой импульсной характеристикой наз. БИХ фильтры (бесконеч. имп. хар-ка).

КИХ фильтры - НЦФ

9. Частотные характеристики цифровых фильтров. Влияние координат нулей и полюсов передаточной функции фильтра на его частотные характеристики. Нормировка по частоте. Переход от нормированной частоты к естественной..

Амплитудно-частотная и фазочастотная характеристики

Представляя комплексную частотную характеристику одномерного скалярного стационарного линейного ЦФ в виде , (3.17)

Получим АЧХ и ФЧХ (3.18) . (3.19)

Амплитудно-частотная характеристика(3.18) одномерного скалярного стационарного линейного ЦФ определяет амплитуду выходного сигнала устойчивого фильтра в установившемся режиме при входном сигнале

(3.20)

а фазочастотная характеристика — сдвиг фазы выходного сигнала относительно фазы входного сигнала в установившемся режиме.

Переход от передаточной функции к функции частоты осуществляется с использованием замен: z = e^jwT.

H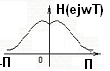 (e^jwT) – частотная характеристика фильтра. В общем случае она комплексная. Частота фильтра будет повторяться с периодом

Так как частотную характеристику представляют в диапазоне от -∞ до +∞, ЧХФ строят от –П до П.

, , , ,

Т.к. H(e^jω2πf) периодична и симметрична, то характеристики строят либо от –π до π, либо (-0.5…0.5).

Частотные характеристики фильтров 1-ого порядка.

Не рекурсивные фильтры:

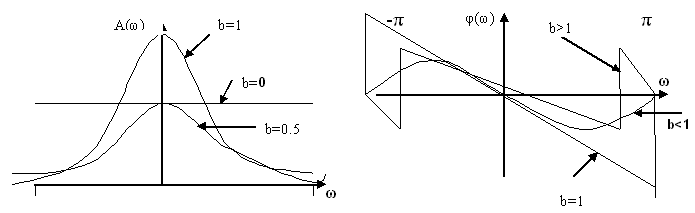
Фазочастотные характеристики в случае b>0 линейны, при b<0 нелинейны. Чем ближе к 1, тем фильтр более идеальный. С ростом b фазовые характеристики приближаются к началу координат.

Рекурсивные фильтры:

АЧХ может принимать положительные значения. Характеристика имеет один экстремум. При переходе через 0 меняется вид экстремума на противоположный. ФЧХ нелинейна.

Частотные характеристики фильтров 2-ого порядка.

Не рекурсивные фильтры:

Координаты min совпадают с фазами полюсов. Размах А(ω) зависит от соотношения b₁ и b₂. Влияние b₂ более сильное.

Характеристика φ(ω)-нелинейна, но в начале координат можно считать линейной. A(ω)-всегда характеристика ФНЧ, даже если b₁=0.

Рекурсивные фильтры:

Частотные характеристики имеют 2 экстремума. В зависимости от коэффициентов a₁ и a₂ положение экстремумов меняется. Координаты экстремума определяются фазой полюсов характеристического уравнения. ФЧХ нелинейна, т.е. такие фильтры непригодны для приёма сигнала без искажения.

Зная характеристики фильтров 1-ого и 2-ого порядка, можно получить характеристики фильтров более высокого порядка, если учесть, что они составляются из произведений характеристик фильтров 1-ого и 2-ого порядка.Если полюс – действительный, то характеристика будет иметь максимум на нулевой частоте и она будет уходить в бесконечность.

Влияние координат нулей и полюсов передаточной функции на АЧХ фильтра.

Р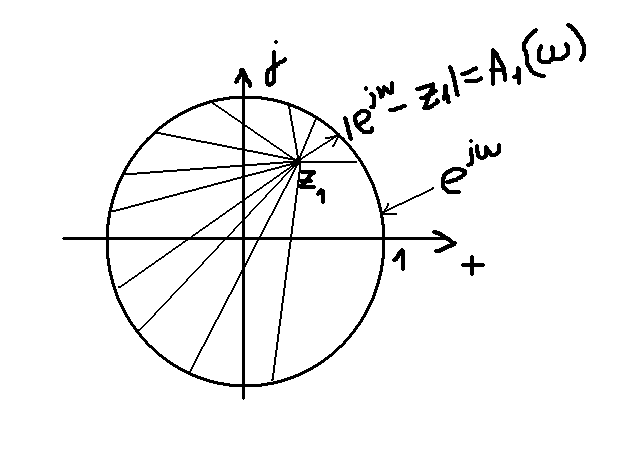 ассмотрим передаточную функцию фильтра: H_z(z) = z – z₁ Найдем его АЧХ.

A₁(w) = e ^jw – z₁

При изменении w, A₁(w) тоже будет изменяться.

Чем ближе полюс к окружности, тем меньше линейность. Если он лежит на окружности, то минимум равен нулю.

Т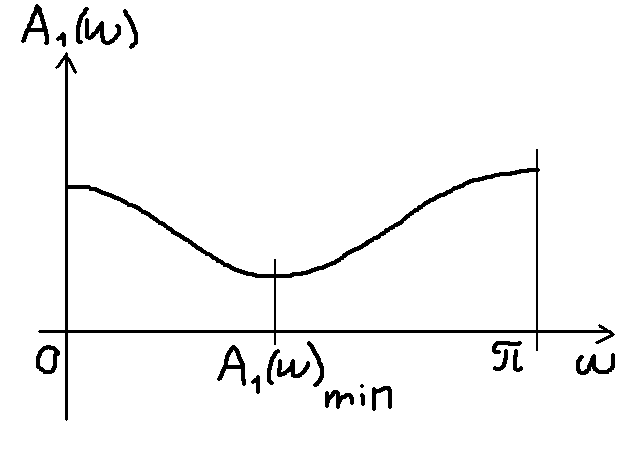 .к. левая полуплоскость находится в круге первого радиуса, а правая – за его пределами, то случай неустойчивости (z₁) находится за пределами первого радиуса. Если система неустойчива, то для нее тоже можно найти частотную характеристику по тем же самым правилам.

Для рекурсивных фильтров, у которых в числителе нет слагаемых z, приравнивая знаменатель к нулю, можно найти корни уравнения, которые называются полюсами. Полюса будут пиками АЧХ. Если фильтр нерекурсивный, то на нулях, являющихся корнями уравнения, АЧХ будет иметь минимумы. Зная положение нулей и полюсов, можно определить выбросы и провалы АЧХ. Таким образом можно учитывать, что выбросы и провалы могут компенсироваться.

К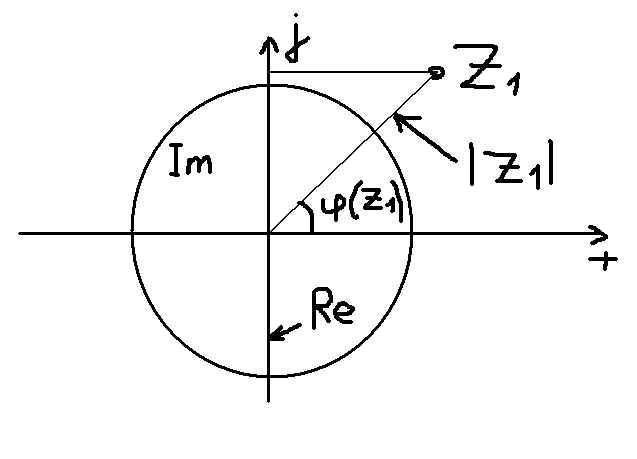 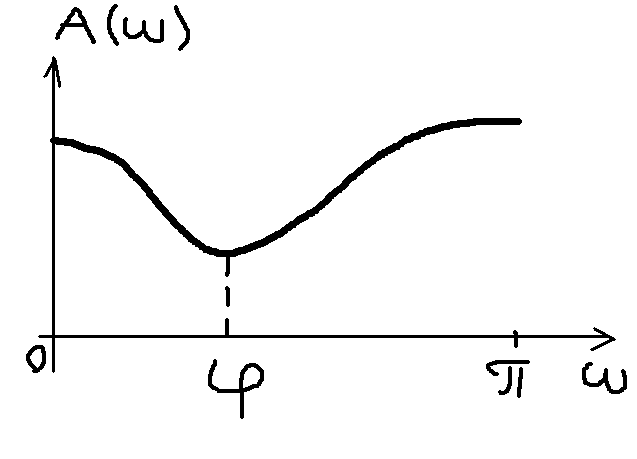аждый полюс характеризуется своей амплитудой и фазой. Выбросы и провалы АЧХ совпадают с фазами полюсов. А величина зависит от амплитуды.

НОРМИРОВКА ПО ЧАСТОТЕ

С целью упрощения сопоставления частотных характеристик различных ЦФ частоту нормируют одним из двух способов [6].

При первом способе вводят нормированную частоту , тогда и требования к частотным характеристикам вещественного ЦФ задаются на интервале нормированных частот — рис.3.3,а, а комплексного ЦФ — на симметричном интервале .

При втором способе применяют нормированную частоту , тогда и требования к частотным характеристикам вещественного ЦФ задаются на интервале нормированных частот — рис.3.3,б, а комплексного ЦФ — на симметричном интерва-ле .

Если производится нормировка частоты, то в обозначениях частотных характеристик ЦФ необходимо соответствующим образом заменить аргументы. Например, при втором способе нормировки следует писать: , , , .

Рис.3.3. Два способа нормировки частоты для частотных характеристик ЦФ

Согласно выражениям (3.21) и (3.22) амплитудно-частотная и фазочастотная характеристики ЦФ являются функциями аргумента , поэтому изменение частоты дискретизации приводит к пропорциональному изменению характерных частот АЧХ и ФЧХ фильтра, например граничных частот полос пропускания и задерживания . Это обстоятельство позволяет осуществлять перестройку ЦФ путем изменения частоты дискретизации . При такой перестройке относительная ширина полосы пропускания у полосового фильтра или же полосы задерживания у режекторного фильтра не изменяется. На практике перестройку ЦФ путем изменения частоты дискретизации можно осуществлять лишь в пределах, пока выполняется условие теоремы отсчётов В.А. Котельникова (1.7).