5. Влияние добавления нулей в исходную последовательность.

Эффект растекания спектра.

Исходную последовательность можно дополнить нулями. Если рассматривать этот сигнал, как временной, то никаких особенностей тут не возникает (как были нули, так и остались). А когда будем находить преобразование Фурье, появятся особенности.

С пектр преобразования Фурье – дискретный. Пусть такой:

После дополнения нулями могут появиться дополнительные составляющие, показанные пунктиром.

Крайняя составляющая f_макс=1/Т (по т.Котельникова) ∆f=1/Tp => частота ↓.

Поскольку при дискретизации сигнала и нахождении дискретного спектра значения составляющих вычисляются только в фиксированных точках, не имеет смысла проводить интерполяцию между точками, т.к. никакого физического смысла полученные т.о. значения спектра не имеют.

В результате дополнения нулями исходной последовательности внутри спектра появляются дополнительные составляющие, и создаются впечатление, что мы получаем спектр с более высокой разрешающей способностью. Но эти дополнительные составляющие присущи уже другому сигналу, который дополнен нулями (а составляющие исходного сигнала остались).

Учитывая особенности полученного спектра, следует стремиться, чтобы исходные данные были бы кратны 2ⁱ или достаточно хорошо приближались снизу (если 14, то 16)

РАСТЕКАНИЕ СПЕКТРА

П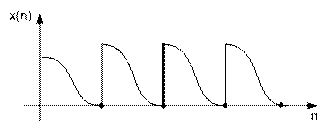 ри ДПФ мы предполагали (умалчивая), что последовательность отсчетов анализируемого сигнала является периодически продолженной вперед и назад во времени. При этом, если значения начальных и конечных отсчетов сигнала сильно отличаются, при периодическом повторении на стыках сегментов возникают скачки, из-за которых спектр сигнал расширяется.  Это явление называется растеканием спектра (spectrumleanage). Проиллюстрируем на примере сигнала

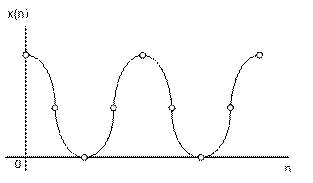
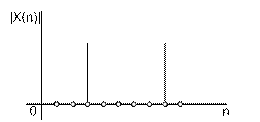
Если анализируемая последовательность содержит точно целое число периодов гармонического сигнала, т.е. если   - целое число, то гармонический сигнал s(t) продолжается без скачков, а если подставить в формулу ДПФ получим Таким образом ДПФ сигнала s(k) в этом случае содержит только 2 отсчета, отличных от нуля. Но если   не целое, то спектр становится значительно более богатым.     Таким образом, подчеркнем еще раз, что причиной растекания спектра является именно периодическая продолжительность сигнала.

Для уменьшения растекания используют окна или взвешивание.

Весовые функции.

Для уменьшения явления растекания спектра при ДПФ применяют весовые функции, которые также называются окнами (windows). В этом случае перед расчетом ДПФ сигнал умножается на весовую функцию w(k), которая должна спадать к краям сегмента. Тогда формула ДПФ принимает вид:

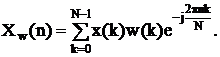(Здесь в степени экспоненты 2*pi*n*k/N) Роль весовой функции можно рассматривать с разных точек зрения. Сначала проанализируем ситуацию во временной области. Если мы используем весовую функцию, которая имеет максимум в середине (при k=N/2) и плавно спадает к краям (k=0, k=N-1), это приведет к ослаблению эффектов, связанных со скачками сигнала при периодическом повторении последовательности, т.е. к уменьшению растекания спектра. Тот же вывод можно сделать и в частотной области. Умножение сигнала на весовую функцию соответствует свертке спектров сигнала и окна. Это приводит к тому, что линии содержащиеся в  спектре несколько расширятся. Однако становится возможным уменьшить уровень боковых лепестков спектральной функции, что и является целью весовой функции. Если трактовать ДПФ как фильтрацию, при использовании весовой функции w(k) получаются частотные характеристики вида

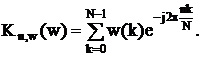(Здесь в степени экспоненты 2*x*n*k/N) Выбирая весовую функцию (окно) определенным образом, можно уменьшить уровень боковых лепестков частотных характеристик фильтров, соответствующих отдельным каналам ДПФ. Платой за это является расширение центрального лепестка частотной характеристики («резиновость» АЧХ).