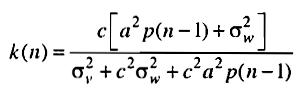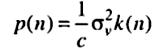- •1. Линейная свертка. Способы вычисления.
- •2. Круговая свёртка. Способы вычисления.
- •3. Дискретное преобразование Фурье. Масштабирование по частоте. Переход от нормированной частоты к естественной
- •4 Быстрое пр-е Фурье.Переход к естеств. Масштабу частот
- •5. Влияние добавления нулей в исходную последовательность.
- •6. Разностное уравнение. Передаточная функция цифрового фильтра(цф). Нерекурсивные и рекурсивные цф. Каноническая форма рекурсивных фильтров.
- •7. Структурные схемы рекурсивных и нерекурсивных цф.
- •Схемы нерекурсивных фильтров
- •8 .Связь между передаточной функцией и импульсной характеристикой. Реакция ф. На произв. Вход-е воздействие.
- •10. Аппроксимация ачх по Баттерворту аналоговый фильтр
- •11. Получение передаточной функции фильтров Баттерворта. Схемы фильтров. Для получения пф поступают так:
- •12.Полиномы Чебышева первого рода. Аппроксимация ими. Требуется, чтобы характеристика фильтра была на всех частотах одинакова. Этим свойством обладают фильтры Чебышева.
- •13 Фильтры Чебышева 2го рода.Элептические фильтры и фильтры Беселя
- •14 Преобразование нормир-го фильтра в фильтры других типов.
- •15. Преобразование аналоговых фильтров в цифровые
- •16. Преобразование аналоговых фильтров в цифровые
- •17. Критерии, используемые при проектировании цф.
- •18.Передаточные функции ких фильтров с линейной фазой
- •19. Однородный фильтр. Виды схемной реализации. Его ачх
- •20. Оптимальный по Чебышеву синтез фильтров.
- •21. Алгоритм Ремеза
- •22 Синтез ких-фильтров методом окон.
- •23. Фильтры с косинусоидальным сглаживанием.
- •24. Преобразование и преобразователи Гильберта
- •25. Задание требований к частотным характеристикам цифровых дифференциаторов Гильберта
- •27.Округление промежуточных результатов в цф.
- •28. Адаптивные фильтры и их применение.
- •29. Задача линейного предсказания. Передаточная функция предсказателя
- •30. Решение задачи линейного предсказания во временной области. Уравнение Юла-Уолкера.
- •31. Определение параметров предсказывающего устройства по методу Левисона-Дарбина.
- •32. Проблемы передачи параметров предсказывающего устройства.
- •33. Линейные спектральные пары. Метод Итакуры
- •34. Постановка задачи адаптивной обработки сигнала.
- •35. Вывод уравнения Винера - Хопфа.
- •36. Постановка задачи Калмановского оценивания сигнала.
- •37. Структурная схема Калмановского фильтра. Формулы для расчёта его коэффициентов.
- •38. Суть параметрического спектрального оценивания. Особенности ар, сс, арсс - спектров.
- •Оценивание параметров сс модели
- •Оценивание пар-ров арсс моделей
- •39. Многоскор-е сис-мы цос.Однократная интерполяция
- •40. Многоскор-е сис-мы цос.Однократная децимация
- •41. Многоскор-е сис-мы цос.Полифазная система структур интерполяции.
- •42. Многоскор-е сис-мы цос.Полифазная система структур децимации
- •43. Постановка задачи речевой обработки сигналов.
- •44. Кратковременные функции энергии, среднего значения, числа переходов через нуль.
- •Оценивание начала и конца слова по кратковременным характеристикам Энергии, среднего значения и числа переходов через нуль.
- •4 6. Оценка основного тона по медианному усреднению.
- •47. Оценивание основного тона на основе специальных временных последовательностей. (метод || обработки)
- •Модель речеобразования на основе линейного предсказания.
- •Системы верификации и идентификации диктора.
36. Постановка задачи Калмановского оценивания сигнала.
Винеровская оценка коэф-тов КИХ-фильтров требует полного пересчета всех авто- и взаимокорреляционных матриц для каждой новой выборки, что с вычислит т.з. нерационально. Если иметь дело с продолжительным рядом отсчетов вх сигнала, значительно более удобными являются рекуррентные алгоритмы получения оценок, вносящие коррекцию на каждом шаге итерационного процесса.
По существу, калмановское оценивание реализует рекурсивную процедуру адаптации. Основанную на авторегрессионной модели процесса генерирования сигнала. Если вх сигнал x(n) явл случ и марковским, то его можно представить в виде выхода ЛДС первого порядка, возбуждаемой белым шумом v(n) с нулевым средним и дисперсией σ2w. Модель генерирования сигнала описывается разностным уравнением 1го порядка.
![]() (28.1)
(28.1)
Устройство генерирования случ сигнала:
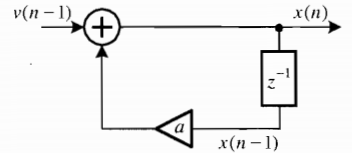
После прохождения канала связи вх сигнал претерпевает амплитудные изменения, описываемые пост коэф-том с, и на него воздействовал аддитивный белый шум v(n). Модель взаимодействия канала на сигнал описываается уравнением: y(n)=cx(n)+ v(n). (28.2)
Модель прохождения сигнала по каналу связи:
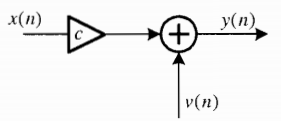
Зашумленный сигнал y(n) поступает на вход синтезируемого адаптивного калмановского фильтра. На его выходе необходимо получить рекуррентную оценку x^(n), максимально близкую к сигналу x(n) по критерию МНК.
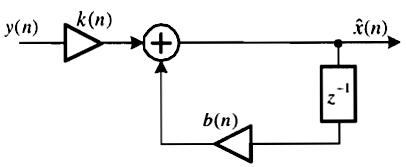
37. Структурная схема Калмановского фильтра. Формулы для расчёта его коэффициентов.


(28.4) – ошибка оценки
(28.5) – среднеквадратич ошибка
(28.3)
в (28.5): -
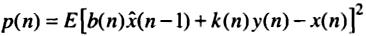
Данное выражение дифф-ся по b(n) и k(n) с последующим приравниванием к нулю:
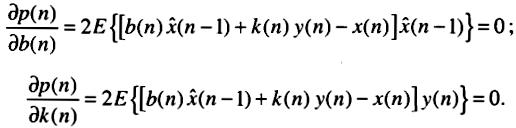
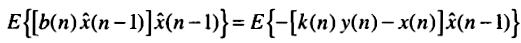
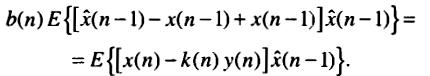
Учитывая,
что
![]() и
с учетом (28.4),
получим:
и
с учетом (28.4),
получим:
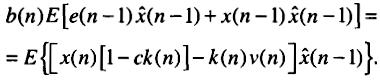
Принцип орготональности, кот минимизирует ошибку, требует некоррелированности ошибки e(n) и оценки x^(n-1), а также независимости шума и x^(n-1), что выполняется в рамках сделанных предположений. Это означает выполнение равенств:
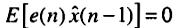
![]()
Тогда предыдущее уравнение примет вид
![]()
Подставив сюда (28.1), получим:
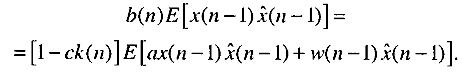 (28.15)
(28.15)
(28.1)
в (28.2) и в (28.3):
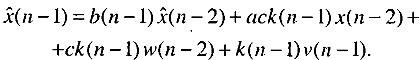 (28.16)
(28.16)
Умножим обе части на w(n-1) и возьмем мат. Ожидание:
![]() (28.17)
(28.17)
Т.к. шум w(n-1) некоррелирован со всеми членами в правой части (28.16).
Преобразуем (28.15) исходя из (28.17)
![]()
Отсюда:
![]() (28.18).
(28.18).
(28.18)
в (28.3) -->
![]()
Это уравнение явл искомым решением для построения адаптивного рекурсивного оценивателя 1го порядка, называемого скалярным фильтром Калмана.
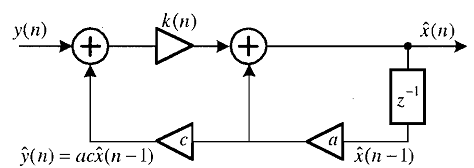
Адаптация здесь происходит след образом: предыдущая оценка x^(n-1) после умножения на коэф-ты а и с предсказывает очередной отсчет зашумленного сигнала y^(n). Последний сравнивается с текущим отсчетом y(n). Разница между ними с коэф-том «доверия» k(n) суммируется с предсказанной оценкой а x^(n-1), в рез-те чего получается текущая оценка x^(n). Изменяющийся во времени k(n) должен зависеть от шумовых параметров модели и текущего значения среднеквадратич ошибки p(n).