25. Задание требований к частотным характеристикам цифровых дифференциаторов Гильберта

_{Особенности ЦПГ:}

1. _{В полосе задержания нет необходимости задавать жесткие требования.}

2. _{Полоса пропускания фильтра должна быть такой же, как полоса пропускания входного фильтра}

3. _{Требования к затуханию не должны быть жестче требований входного фильтра.}

//дополнительно//

//далее по требованиям//

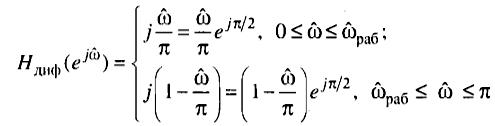
Это частотная хар-ка диф-ра.

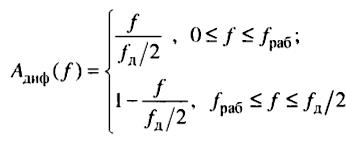
Это АЧХ диф-ра в обл-ти ненормированных частот. ФЧХ постоянна и равна Пи/2.

Задание требований:

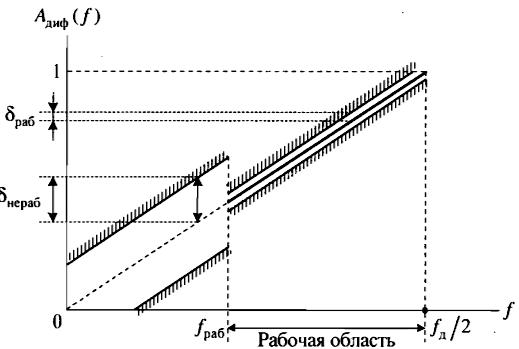
По расположению рабочей области, в пределах которой задаются требования к АЧХ, выделяют широкополосные (0 – f_д/2), низкочастотные (0 << f_д/2), полосовые (fраб1>0 и fраб2< f_д/2) и высокочастотные (fраб>>0 и f= f_д/2) диф-ры. Особенности задания требований к ЦД в том, что требования к АЧХ в рабочей обл-ти предъявляются достаточно жесткие, а вне рабочей обл-ти АЧХ не контролируется.

Ш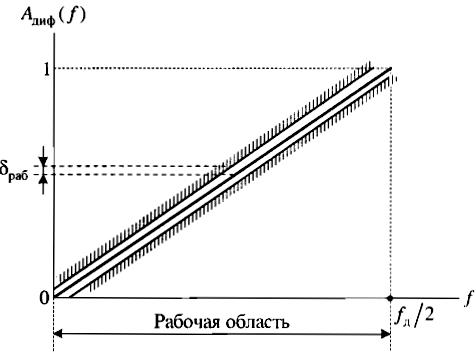 ирокополосные:

Низкочастотные:

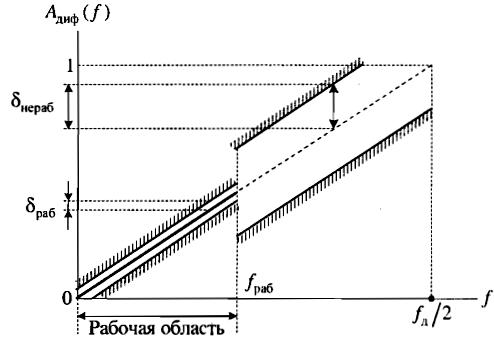
П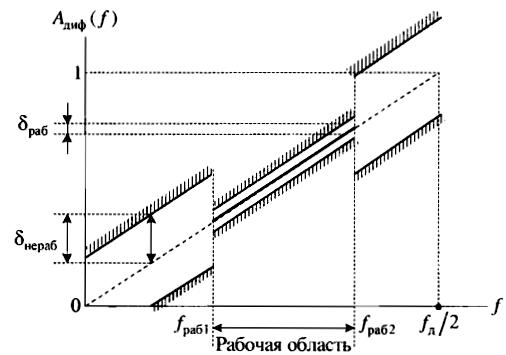 олосовые:

Высокочастотные:

26. Масштабирование коэффициентов ЦФ. Постановка задачи. Методы определения величины коэффициента масштабирования с использованием импульсной переходной характеристики. Влияние масштабирования на АЧХ фильтра.

Коэф. фильтра могут иметь произвольное значение. Может оказаться что коэф-ты выходят за пределы разрядной сетки. Для устранения этого применяют масштабирование [-1;1].

1) Масштабирование с использованием ИХ.

h(n) ;

Т.к. испол. сетка с фиксированной запятой, то .

И Если это не выполняется, то , где - коэф. маштабирования.

2) Масштабирование по макс. сигнала.

Применяется для систем не высокого порядка (< 5)

Тогда . ;

Zn=0,5 => максимум на 0 частоте

,

В системах с более высоким порядком сложно выявить частоту на которой имеется максимум.

Коэфф. имеющие малые значения, могут потерять значительное число значений. Если умножить на 4 справа, мы не получим точного коэф. В результате существенно изменится ЧХ фильтра. Если фильтр реализовать в виде биквадратных звеньев, то влияние масштабирования будет сказываться меньше. Эо объясняется тем, что в отдельном биквадратном блоке разброс коэф. будет меньше.

27.Округление промежуточных результатов в цф.

При работе цифрового фильтра производится много промежуточных сложений и умножений и промежуточные результаты могут существенно превосходить входные и выходные сигналы фильтра, что приводит к переполнению разрядной сетки. Если фильтр с общими линейными задержками, то в нем вначале производится вычисление на рекурсивной цепи, а затем в нерекурсивной сигналы, которые хранятся в л.з. могут быть очень большими. Уменьшить переполнение можно применением представления чисел с плавающей запятой, при этом усложняется ариф. устройство.

Если использовать формат с плавающей запятой, то операции сложения могут приводить к потере точности. При сложении чисел с плавающей запятой может оказаться, что результат зависит от порядка чисел. Чтобы это исключить существует правило, что сначала надо складывать по модулю малые числа, затем большие. Но в цифровых фильтрах это правило не применимо, т.к. мы не можем проконтролировать какие числа в данный момент складываются в фильтре.

Округление промежуточных результатов. Фильтры имеют промежуточные результаты, которые хранятся для выполнения последовательных действий и такое хранение требует применение округления результатов. Если используется формат с фиксированной запятой, то операция сложения и вычитания не приводит к необходимому округлению, а могут выполнить переполнение разрядной сетки. Операции * и / сохраняют силу, но операции «+» тоже могут привести к потере точности.

ВОПРОС: в большую сторону или отбросить.

10,1100 2,75

01,0101 1,3125

100,0001 4,0625

Такие задачи приводят к тому, что результат суммирования нескольких чисел может зависеть от порядка их складывания.

Существует правило, что сложение надо начинать с меньших чисел, тогда будет меньше потерь. Но у нас не получится, поскольку нельзя предсказать какие цифры появятся при изменении фильтра.

Многие проблемы, связанные с квантованием коэффициентов и округлением промежуточных результатов можно значительно уменьшить, если фильтры реализованные в канонической форме, а в виде последовательно соединенных биквадратных блоков.

Предельные циклы

Округление коэффициентов и результатов вычислений, которые естественно возникают, может приводить к появлению так называемых предельных циклов для вполне устойчивых фильтров.

Например: пусть есть фильтр

- рекурсивный фильтр, его полюс 0.95

Фильтр устойчив. Пусть входной сигнал отсутствует, а внутренне состояние фильтра равно13. Тогда

Покажем, что выходной сигнал фильтра ограничивается только целочисленными значениями.

y(1) = 0.95∙y(0) = 0.95∙13 = [12,35] = 12

y(2) = 0.95∙y(1) = 0.95∙12 = [11,4] = 11

y(3) = 0.95∙y(2) = 0.95∙11 = [10,45] = 10

y(4) = 0.95∙y(3) = 0.95∙10 = [9,5] = 10

Если заменить в исходном уравнении знак на минус, то получим в конце чередование +10, -10… Существует 2 типа предельных циклов. Зернистый предельный циклы возникают, когда выходной сигнал фильтра при отсутствии входного сигнала затухал бы, но из-за округление результатов это затухание не доходит до нуля. Переполнение циклы возникают, когда из-за округления результатов выходной сигнал фильтра начинает возрастать. И происхождение сигнал фильтра начинает возрастать. Для анализа возможности возникают предельные циклы. Используют понятия эффект. значения коэффициентов. Под эффективным значением коэфф. понимают отношение округленного результата умножения к использ. в качестве множителя значение внутреннего состояния фильтра. Это значение может быть разным для разных состояний фильтра.

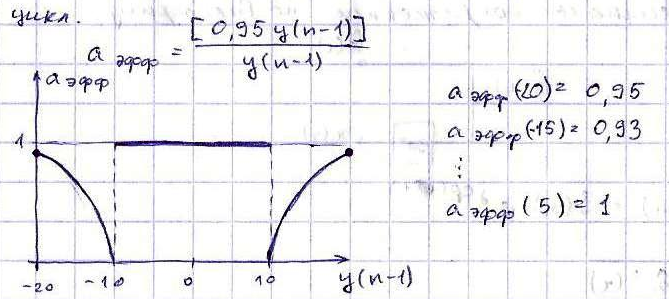
Если для какого-то внутреннего состояния набор эффективных значений коэффициентов приводит к появлению полиса располож. На окружн. Единич. Радиуса, это означает что данное внутреннее состояние дает предельный цикл.