1. Линейная свертка. Способы вычисления.

Свёртка фу́нкций — операция в функциональном анализе, показывающая «схожесть» одной функции с отражённой и сдвинутой копией другой. Понятие свёртки обобщается для функций, определённых на группах, а также мер. В математике, свёртка — это математическая операция двух функций f и g, порождающая третью функцию, которая обычно может рассматриваться как модифицированная версия одной из первоначальных. По существу, это особый вид интегрального преобразования.

Свертка позволяет рассчитать сигнал s(t) на выходе линейного фильтра с импульсной характеристикой h(t) , при входном сигнале x(t).

При обработке сигнала с помощью ЭВМ всегда будем иметь дело с дискретными входными последовательностями  мат. операции будут проводиться в дискретном виде. По своему назначению дискретная и непрерывная свертки совпадают. В дискретном случае различают два вида сверток: линейную (или апериодическую) и циклическую. Циклическую свертку еще часто называют круговой или периодической.

В общем случае дискретная свертка:

- один из сигналов сдвинут.

Различают 2 вида дискретной свертки: линейную и круговую:

-круговая

-линейная

При линейной свёртке периодических повторений сигналов нет.

Длина свёртки : N = N1 + N2 – 1. Найдём линейную свёртку для рассмотренного примера: x₁(n)=0,1,2; x₂(n)=1,0,-1

обозначается

Y(0)=x₁(0)*x₂(0) =0*1=0

Y(1)=x₁(0)*x₂(1)+x₁(1)*x₂(0) =0*0+1*1=1

Y(2)=x₁(0)*x₂(2)+x₁(1)*x₂(1)+x₂(2)*x₂(0)=0*(-1)+1*0+2*1= 2

Y(3)=x₁(0)*x₂(3)+x₁(1)*x₂(2)+x₁(2)*x₂(1)=0*0+1*(-1)+2*0= -1

Y(4)=x₁(0)*x₂(4)+x₁(1)*x₂(3)+x₁(2)*x₂(2)=0*0+1*0+2*(-1)= -2

Способы вычисления линейной свертки.

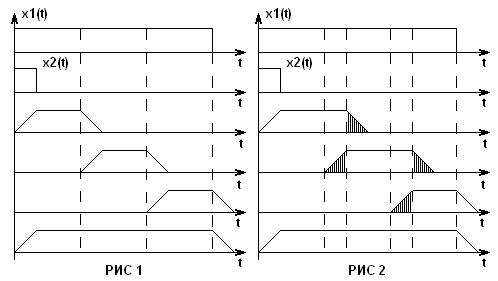
1) метод суммирования с накоплением (РИС 1). Здесь исходная последовательность разбивается на ряд не перекрывающихся сегментов. В каждом сегменте вычисляется свертка. Если x₁ содержит N₁ значений, а x₂ сод-жит N₂ то свертка сегмента х₂ с х₁ будет содержать N₁+N₂-1 значений. Если найдем такую же свертку для следующего сегмента, то соседние свертки будут перекрываться на N₂-1 отсчетов и на этом участке их суммы надо сложить. Недостаток в том, что приходится суммировать не нулевые значения.

2) метод суммирования с отбрасыванием (РИС 2). Также производится секционирование одной из последовательностей, но секции перекрываются на величину 2-й последовательности. В результате этого начальные участки в результирующей последовательности на следует учитывать  их отбрасывают при получении результирующей свертки.

2. Круговая свёртка. Способы вычисления.

Свёртка фу́нкций — операция в функциональном анализе, показывающая «схожесть» одной функции с отражённой и сдвинутой копией другой. Понятие свёртки обобщается для функций, определённых на группах, а также мер. В математике, свёртка — это математическая операция двух функций f и g, порождающая третью функцию, которая обычно может рассматриваться как модифицированная версия одной из первоначальных. По существу, это особый вид интегрального преобразования.

Свертка позволяет рассчитать сигнал s(t) на выходе линейного фильтра с импульсной характеристикой h(t) , при входном сигнале x(t).

При обработке сигнала с помощью ЭВМ всегда будем иметь дело с дискретными входными последовательностями  мат. операции будут проводиться в дискретном виде. По своему назначению дискретная и непрерывная свертки совпадают. В дискретном случае различают два вида сверток: линейную (или апериодическую) и циклическую. Циклическую свертку еще часто называют круговой или периодической.

В общем случае дискретная свертка:

- один из сигналов сдвинут.

Различают 2 вида дискретной свертки: линейную и круговую:

-круговая

-линейная

При круговой свёртке один из сигналов представляется периодически продолженным в обе стороны. Рассмотрим круговую свертку: полагаем, что обе последовательности имеют одинаковую длину N. Круговая также имеет длину N. Если в круговой свертке (n-k)<0, то вместо него берут n-k+N.

Пример: x₁(n)=0,1,2; x₂(n)=1,0,-1

обозначается

y (0)=x₁(0)*x₂(0)+x₁(1)x₂(2)+x₁(2)x₁(1)=0*1+1*(-1)+2*0= -1

y(1)=x₁(0)*x₂(1)+x₁(1)*x₂(0)+x₁(2)*x₂(2)=0*0+1*1+2*(-1)= -1

y(2)=x₁(0)*x₂(2)+x₁(1)*x₂(1)+x₁(2)*x₂(0)=0*(-1)+1*0+2*1= 2

y(3)=y(0)

За счёт периодичности сигнала y(n) также периодически повторяется.

Если одна из последовательностей имеет размер N₁>N₂, то целесообразно зеркально отображать 2-ю последовательность, а 1-ю периодически повторять. Длина круговой свертки будет определятся наибольшим значением. В случае, если длины последовательностей N велики, то применяют алгоритм вычисления круговой свертки, основанный на преобразовании Фурье:

Используя этот алгоритм вычисляют:

1)

2)

3) Обратное преобразование: