14.Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейными однородными дифурами второго порядка с постоянными коэффициентами называются уравнения вида:

y’’+py’+qy=0, где p и q – некоторые числа.

Составим характеристическое уравнение:

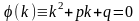, которое получается из данного уравнения путем замены в нем производных искомой функции соответствующими степенями “к”. Причем сама функция заменяется единицей.

Если к1 и к2 – корни характериситического уравнения, то общее решение однородного уравнения имеет один из следующих трех видов:

1). 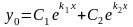, если к1 и к2 – действительные и различные, т.е. 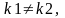D>0.

2). , если к1 и к2 – действительные и равные, т.е. к1=к2, D=0.

3). , если к1 и к2 – комплексные, т.е. 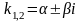; D<0.

15.

Общее решение линейного однородного дифференциального уравнения   с непрерывными на интервале интегрирования X коэффициентами   определяется линейной комбинацией 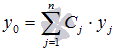 , где   - линейно независимые частные решения ЛОДУ на X, а   - произвольные постоянные. Таким образом, общее решение линейного однородного дифференциального уравнения второго порядка   с постоянными коэффициентами имеет вид y₀ = C₁ ⋅ y₁ + C₂ ⋅ y₂ , где y₁ и y₂ – частные линейно независимые решения, а С₁ и C₂ – произвольные постоянные. Осталось научиться находить частные решения y₁ и y₂. Эйлер предложил искать частные решения в виде  . Если принять   частным решением уравнения  , то при подстановке этого решения в уравнение мы должны получить тождество. 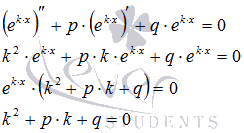  Так мы получили характеристическое уравнение. Решения k₁ и k₂ этого квадратного уравнения определяют частные решения   и   нашего ЛОДУ второго порядка с постоянными коэффициентами. В зависимости от коэффициентов p и q корни характеристического уравнения могут быть:

действительными и различными  ,

действительными и совпадающими  ,

комплексно сопряженной парой  .

В первом случае линейно независимыми частными решениями исходного дифференциального уравнения являются   и  , общее решение ЛОДУ второго порядка с постоянными коэффициентами есть  . Функции   и   действительно линейно независимы, так как определитель Вронского 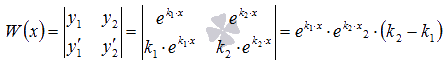  отличен от нуля для любых действительных x при  . Во втором случае одним частным решением является функция  . В качестве второго частного решения берется  . Покажем, что   действительно является частным решением ЛОДУ второго порядка с постоянными коэффициентами   и докажем линейную независимость y₁ иy₂. Так как k₁ = k₀ и k₂ = k₀ совпадающие корни характеристического уравнения, то оно имеет вид  . Следовательно,   - исходное линейное однородное дифференциальное уравнение.

…….

Если имеется однородное линейное дифференциальное уравнение c постоянными коэффициентами

р₀у⁽ⁿ⁾ + p₁y^(n-1) + … + p_ny = 0,

то  алгебраическое уравнение

p₀λⁿ + p₁λ^n-1 + … + p_n = 0

называется его характеристическим уравнением.

…………

. Корни характеристического уравнения действительные и кратные

Пусть характеристическое уравнение L(λ) = 0 степени n имеет m корней λ₁, λ₂,..., λ_m, кратность которых, соответственно, равна k₁, k₂,..., k_m. Ясно, что выполняется условие

Тогда общее решение однородного дифференциального уравнения с постоянными коэффициентами имеет вид

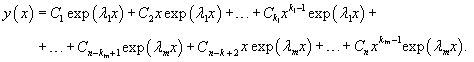
Видно, что в формуле общего решения каждому корню λ_i кратности k_i соответствует ровно k_i членов, которые образуются умножением x в определенной степени на экспоненциальную функцию exp(λ_i x). Степень xизменяется в интервале от 0 до k_i − 1, где k_i − кратность корня λ_i.