
- •5. Дифференциальные уравнения первого порядка с разделяющимися переменными.
- •6. Однородные дифференциальные уравнения первого порядка.
- •11.Три случая понижения порядка.
- •13.Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •14.Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •20. Системы дифференциальных уравнений
- •Метод Коши
- •28. Метод функций Ляпунова при исследовании на устойчивость точки покоя нелинейной системы ду.
- •47. Комплексная форма ряда Фурье
- •51. Интеграл по комплексной переменной.Свойства
- •52 Интегральная теорема Коши для односвязной и многосвязной области.
- •53 Интеграл Коши. Интегральная формула Коши.
- •Классификация изолированных особых точек однозначной функции.
- •1. Для того чтобы точка а была устранимой особой точкой функции f (z), необходимо и достаточно, чтобы лорановское разложение этой функции в окрестности точки а не содержало главной части.
- •3. Точка а тогда и только тогда является существенно особой, когда главная часть лорановского разложения функции f (z) в окрестности этой точки содержит бесконечно много отличных от нуля членов.
- •58 Основная теорема теории вычетов
- •Задача Коши для ду 1-ого порядка. Теорема существования и единственности решения задачи Коши для ду 1-ого порядка.
1. ОСНОВНЫЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ
Дифференциальным
уравнением (ДУ) называется уравнение,
связывающее независимую переменную
 ,
искомую функцию
,
искомую функцию
 и ее производные или дифференциалы.
и ее производные или дифференциалы.
Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение.
Например:
 - диф. уравнение 1-го порядка;
- диф. уравнение 1-го порядка;
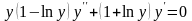 - ДУ 2-го порядка;
- ДУ 2-го порядка;
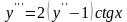 - ДУ 3-го порядка.
- ДУ 3-го порядка.
Дифференциальным уравнением п-го порядка называется соотношение вида
|
(2.1) |
между независимой
переменной
,
функцией
и ее производными
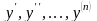 .
.
Если неизвестная
функция в уравнении (2.1) зависит от одной
независимой переменной
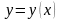 ,
то дифференциальное уравнение называется
обыкновенным дифференциальным уравнением,
если от нескольких переменных
,
то дифференциальное уравнение называется
обыкновенным дифференциальным уравнением,
если от нескольких переменных
 ,
то дифференциальное уравнение называется
уравнением в частных производных. Мы
будем рассматривать только обыкновенные
ДУ и их системы.
,
то дифференциальное уравнение называется
уравнением в частных производных. Мы
будем рассматривать только обыкновенные
ДУ и их системы.
Если уравнение
(2.1) удается разрешить относительно
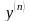 ,
то получим уравнение, разрешённое
относительно старшей производной,
,
то получим уравнение, разрешённое
относительно старшей производной,
|
(2.2) |
Решением
дифференциального уравнения называют
функцию ,
определенную на интервале
,
определенную на интервале
 вместе
со своими производными до п-го
порядка включительно, и такую, что
подстановка функции
в ДУ превращает последнее в тождество
вместе
со своими производными до п-го
порядка включительно, и такую, что
подстановка функции
в ДУ превращает последнее в тождество
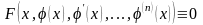 .
.
Процесс нахождения решений дифференциального уравнения называется интегрированием этого уравнения.
Задача нахождения решения уравнения (2.2) или (2.1), удовлетворяющего начальным условиям,
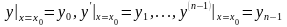 ,
,
где
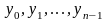 - заданные числа, называется задачей
Коши для дифференциального уравнения.
- заданные числа, называется задачей
Коши для дифференциального уравнения.
Функцию
 ,
где
,
где
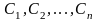 - произвольные постоянные, будем называть
общим решением уравнения (2.1), если
в
при соответствующем выборе постоянных
- произвольные постоянные, будем называть
общим решением уравнения (2.1), если
в
при соответствующем выборе постоянных
 эта функция обращается в решение любой
задачи Коши, поставленной для данного
уравнения, при
эта функция обращается в решение любой
задачи Коши, поставленной для данного
уравнения, при
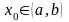 .
.
Решение, полученное из общего при конкретных значениях произвольных постоянных (в частности, всякое решение задачи Коши), называется частным решением (частным интегралом) этого уравнения.
2.Задача Коши для ДУ 1-ого порядка. Теорема существования и единственности решения задачи Коши для ДУ 1-ого порядка.
Для существования
решения задачи Коши для ДУ
 достаточно, чтобы правая часть его, то
есть функция
достаточно, чтобы правая часть его, то
есть функция
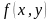 ,
была непрерывна в окрестности начальной
точки, тогда её решение будет определено
(и непрерывно дифференцируемо) в общем
случае лишь в некоторой окрестности
начального значения независимой
переменной. А для единственности решения
этого мало. Приведём теорему, которая
обеспечивает существование и единственность
решения задачи Коши.
,
была непрерывна в окрестности начальной
точки, тогда её решение будет определено
(и непрерывно дифференцируемо) в общем
случае лишь в некоторой окрестности
начального значения независимой
переменной. А для единственности решения
этого мало. Приведём теорему, которая
обеспечивает существование и единственность
решения задачи Коши.
Теорема. Если
правая часть ДУ
определена и непрерывна в прямоугольнике
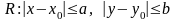 ,
где
,
где
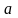 и
и
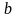 - заданные положительные числа,
удовлетворяет в нем двум условиям:
- заданные положительные числа,
удовлетворяет в нем двум условиям:
непрерывна и ограничена, т.e.
 ;
;
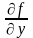 существует и ограничена, т.e.
существует и ограничена, т.e.
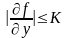 ,
,
где
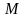 и
и
 - постоянные положительные числа, то
уравнение
имеет единственное решение
,
удовлетворяющее начальным условиям
- постоянные положительные числа, то
уравнение
имеет единственное решение
,
удовлетворяющее начальным условиям
 ,
определенное и непрерывно дифференцируемое
в интервале
,
определенное и непрерывно дифференцируемое
в интервале
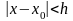 ,
где
,
где
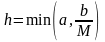 .
.
Теорема(о
существовании и единственности решения
задачи Коши) – пусть функция
определена
и имеет непрерывную частную производную
в области
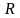 ,
тогда найдётся интервал (х0-б;
х0+б) на котором существует
единственное решение
диф. Уравнения, удовлетворяющее условию
.
,
тогда найдётся интервал (х0-б;
х0+б) на котором существует
единственное решение
диф. Уравнения, удовлетворяющее условию
.
Если правая часть уравнения удовлетворяет в области условиям теоремы существования и единственности, то это уравнение, очевидно, не имеет особых решений.
В частности, если - многочлен, то уравнение не имеет особых решений в области .
Если в уравнении
функция
непрерывна по
и
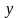 и имеет частную производную по
,
то особыми решениями могут быть те
кривые
,
во всех точках которых
обращается в бесконечность
и имеет частную производную по
,
то особыми решениями могут быть те
кривые
,
во всех точках которых
обращается в бесконечность
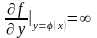 .
.
3. Геометрическая интерпритация ДУ 1-го порядка. Метод изоклин.
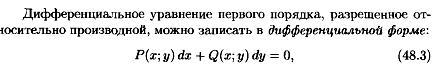

Задача построения интегральной кривой часто решается введением изоклин. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и тоже направление.
Семейство
изоклин дифференциального уравнения
![]() (1)определяется уравнением
(1)определяется уравнением
![]() (2)
(2)
где ![]() —
параметр. Придавая параметру
близкие
числовые значения, получаем достаточно
густую сеть изоклин, с помощью которых
можно приближенно построить интегральные
кривые дифференциального yравнения
(1).
—
параметр. Придавая параметру
близкие
числовые значения, получаем достаточно
густую сеть изоклин, с помощью которых
можно приближенно построить интегральные
кривые дифференциального yравнения
(1).
4. Задача Каши для ДУ n-го порядка. Общее решение, частное решение, особое решение ДУ n-го порядка.
Найти решение y=y(x)уравнения F(x, y´,y´´…)=0 (1) удовлетворяющее условие:
y=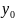
y´= (3)
(3)
y´´=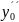 при х=
при х= , где х0, у0,….
, где х0, у0,….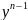 – заданные числа, которые называют
начальные данные решения начальных
условия (3)
– заданные числа, которые называют
начальные данные решения начальных
условия (3)
общим решением диференциального уравнения n-го порядка называется функция
y=𝞿(x, C1, C2,…Cn) (4)
При любых значениях производных постоянных С1, С2,…Сn обращается уравнение (1) в тождество.
Значение С1, С2,..Сn можно подобрать так чтобы она удовлетворяла условиям (3).
Определение: часным решением дифференциального уравнения n-го порядка называется решение полученное из общего решения (4) при фиксированных значениях производных постоянных y=𝞿(x, C1, C2,…Cn), где С1, С2,…Сn – некоторые числа.
Замечание: решениедиференциального уравнения n-го порядка в каждой точке которого нарушается единство решения задачи Каши называется особым.
Определение: Общим интегралом ДУ общего порядка называется уравнение вида:
Ф(х, у, С1, С2…Сn) =0 (5)
не явно определяющее общее решение: y=𝞿(x, C1, C2,…Cn)
Часным решением du n-го порядка называется соотношение Ф(х, у, С1, С2…Сn) =0, которое получается из общего интеграла путем фиксированного значения.
5. Дифференциальные уравнения первого порядка с разделяющимися переменными.
Дифференциальные
уравнения первого порядка в общем виде
можно записать либо через производные
F(x,y,y’)=0,
либо через дифференциалы
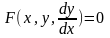 .
.
Дифференциальное уравнение- уравнение с разделяющимися переменными, если его можно представить в виде:
-
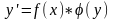 -
через производную.
-
через производную.
-
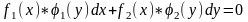 -
через дифференциал.
-
через дифференциал.
В этих уравнениях в произведениях стоят функции, каждая из которых зависит от одной переменной (х или у). Т.е. уравнение будет уравнением с разделяющимися переменными, если его можно преобразовать так, чтобы в одной его части была только одна переменная, а в другой – только другая.
Замечание. При решении дифференциальное уравнение ответу можно придать различную форму в зависимости от того, как записана произвольная постоянная С.
Решение.
-
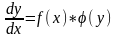 ;
;
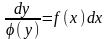 -интегрируем
и получаем решение.
-интегрируем
и получаем решение.

-
 ;
;
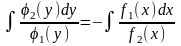
6. Однородные дифференциальные уравнения первого порядка.
Функция f(x,y)
называется однородной функцией n–го
измерения, если при любом
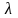 выполняется условие:
выполняется условие:
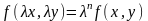 .
.
Дифференциальное уравнение y’=f(x,y) есть однородное, если функция f(x,y) является однородной функцией нулевого измерения.
Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 однородное, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения.
P(x,y)dx=-Q(x,y)dy;

Однородное
уравнение всегда можно привести к виду
 и с помощью замены
и с помощью замены
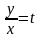 однородное уравнение всегда приводится
к уравнению с разделяющимися переменными
(
;
y=xt; y’=t+xt’).
однородное уравнение всегда приводится
к уравнению с разделяющимися переменными
(
;
y=xt; y’=t+xt’).
7. Линейные ДУ 1-го порядка (метод подстановки Бернулли, метод вариации произвольной постоянной Лагранжа).
ОПРЕДЕЛЕНИЕ. Уравнение вида: y'+p(x)у=q(х) (1)
где р(х) и q(х) — непрерывные функции, называется линейным дифференциальным уравнением первого порядка. Название уравнения объясняется тем, что неизвестная функция у и ее производная у' входят в уравнение линейно, т. е. в первой степени.
ОПРЕДЕЛЕНИЕ. Если q(х) = 0, то уравнение (1) называется линейным однородным уравнением. Если q(х)≠0, то уравнение (1) называется линейным неоднородным уравнением. Для нахождения общего решения уравнения (1) может быть применен метод вариации постоянной. В этом методе сначала находят общее решение линейного однородного уравнения:
у'+р(х)у=0 (2)
соответствующего данному неоднородному уравнению (1). Уравнение (2) является уравнением с разделяющимися переменными. Разделяя переменные и интегрируя, имеем:
![]() =-p(x)dx
⇒ ln|y|=-∫p(x)dx+ln|C1|
Отсюда, потенцируя, находим общее
решение данного уравнения:
y=±C1e-∫p(x)dx,
или y=Ce-∫p(x)dx (3)
=-p(x)dx
⇒ ln|y|=-∫p(x)dx+ln|C1|
Отсюда, потенцируя, находим общее
решение данного уравнения:
y=±C1e-∫p(x)dx,
или y=Ce-∫p(x)dx (3)
где С=±C1 — произвольная постоянная.Теперь найдем общее решение уравнения (1) в виде (3), где С будем считать не постоянной, а новой неизвестной функцией от х (в этом смысл метода!), т. е. в виде y=C(x)e-∫p(x)dx (4)
Чтобы найти функцию С(х) подставим решение в виде (4) в уравнение (1). Получим:
C'(x)e-∫p(x)dx-C(x)p(x)e-∫p(x)dx+p(x)C(x)e-∫p(x)dx=q(x) (5)
Или C'(x)=q(x)e∫p(x)dx (5')
Итак, чтобы функция (4) являлась решением уравнения (1), функция С(х) должна удовлетворять уравнению (5). Интегрируя его, находим: C(x)=q(x)e∫p(x)dxdx+C1
где C1 — произвольная постоянная. Подставляя найденное выражение для С (х) в соотношение (1), получаем общее решение линейного уравнения (1): y(x)=C1e-∫p(x)dx+e-∫p(x)dx∫q(x)e∫p(x)dxdx
Метод И. Бернулли
Суть заключается в следующем. Решение уравнения (1) ищется в виде произведения двух других функций, т.е. с помощью постановки (подстановка Бернулли): y=u(x)+v(x)
где u(x), v(x) - неизвестные функции от x, причем одна из них произвольна. Тогда y'=u'v+uv' Подставляя выражения для y и y' в уравнение (10), получаем:
u'v+uv'+p(x)uv=q(x) или u'v+u(v'+p(x)v)=q(x) (6)
Выберем функцию v(x) так, чтобы сумма в скобках обратилась в нуль, т.е. v'+p(x)v=0. Итак,
![]() +p(x)v=0,
т.е.
+p(x)v=0,
т.е. ![]() =-p(x)dx.
Интегрируя, получаем: ln|v|=-∫p(x)dx+ln|c|.
Ввиду
свободы выбора функции v(x), можно принять
c=1. Отсюда v=e-∫p(x)dx. Подставляя
найденную функцию v в уравнение (1),
получаем u'e-∫p(x)dx=q(x). Получено
уравнение с разделяющимися переменными.
Решаем его: u=∫q(x)e∫p(x)dx. Возвращаясь
к переменной y, получаем решение исходного
дифференциальное уравнения.
=-p(x)dx.
Интегрируя, получаем: ln|v|=-∫p(x)dx+ln|c|.
Ввиду
свободы выбора функции v(x), можно принять
c=1. Отсюда v=e-∫p(x)dx. Подставляя
найденную функцию v в уравнение (1),
получаем u'e-∫p(x)dx=q(x). Получено
уравнение с разделяющимися переменными.
Решаем его: u=∫q(x)e∫p(x)dx. Возвращаясь
к переменной y, получаем решение исходного
дифференциальное уравнения.
y=u•v=(∫q(x)•e∫p(x)dxdx+c)•e-∫p(x)dx
8. Уравнение Бернулли
Обыкновенное дифференциальное уравнение вида:
![]()
называется уравнением
Бернулли (при ![]() или
или ![]() получаем
неоднородное или однородное линейное
уравнение). При
получаем
неоднородное или однородное линейное
уравнение). При ![]() является
частным случаем . Названо в честь Якоба
Бернулли, опубликовавшего это
уравнение в 1695 году. Метод решения с
помощью замены, сводящей это уравнение
к линейному, нашёл его брат Иоганн
Бернулли в 1697 году.[1]
является
частным случаем . Названо в честь Якоба
Бернулли, опубликовавшего это
уравнение в 1695 году. Метод решения с
помощью замены, сводящей это уравнение
к линейному, нашёл его брат Иоганн
Бернулли в 1697 году.[1]
Метод решения
Первый способ:
Разделим все
члены уравнения на
![]() получим:
получим:
![]()
Делая замену:
![]()
и дифференцируя,
получаем:
![]()
Это уравнение
приводится к линейному:
![]()
и может быть решено методом Лагранжа (вариации постоянной) или методом интегрирующего множителя.
Второй способ:
Заменим
![]() тогда:
тогда:
![]()
Подберем ![]() так,
чтобы было
так,
чтобы было
![]()
для этого
достаточно решить уравнение с
разделяющимися переменными 1-го порядка.
После этого для определения ![]() получаем
уравнение
получаем
уравнение ![]() —
уравнение с разделяющимися переменными.
—
уравнение с разделяющимися переменными.
9.Уравнения в полных дифференциалах.

10.Дифференциальные уравнения высших порядков. Теорема о существовании и единственности решения. Задача Коши.



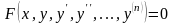 .
. 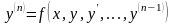 .
.