Каноническое уравнение гиперболы в декартовой системе координат (вывод)

ОПРЕДЕЛЕНИЕ. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от которых до двух фиксированных точек плоскости и есть величина постоянная и равная ( ).

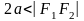Точки и называют фокусами гиперболы.

Получим уравнение гиперболы. Выберем декартову прямоугольную систему координат так, чтобы фокусы и лежали на оси на одинаковом расстоянии от начала координат. В такой системе координат точки и будут иметь координаты:

и ,

где . Пусть – текущая точка гиперболы. По определению гиперболы

,

⇒ ,

⇒ ,

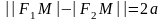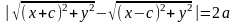Избавимся от квадратных корней:

,

⇒ ,

⇒ .

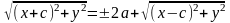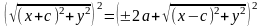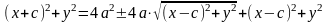Приведя подобные слагаемые, получим:

.

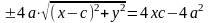Снова возведем обе части в квадрат и приведем подобные слагаемые:

,

⇒ ,

⇒ ,

⇒ .

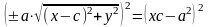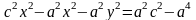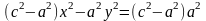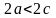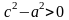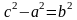Так как по определению , то . Следовательно, , для некоторого числа , и последнее равенство примет вид: .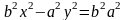

Разделим обе части этого равенства на и окончательно получим:

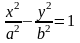. (59)

Уравнение (59) называется каноническим уравнением гиперболы. Система координат, в которой гипербола имеет такое уравнение, называется ееканонической системой координат.

33.